Nuclear Radius & Density (OCR A Level Physics): Revision Note
Exam code: H556
Nuclear Radius
The radii of some nuclei are shown in the table below:
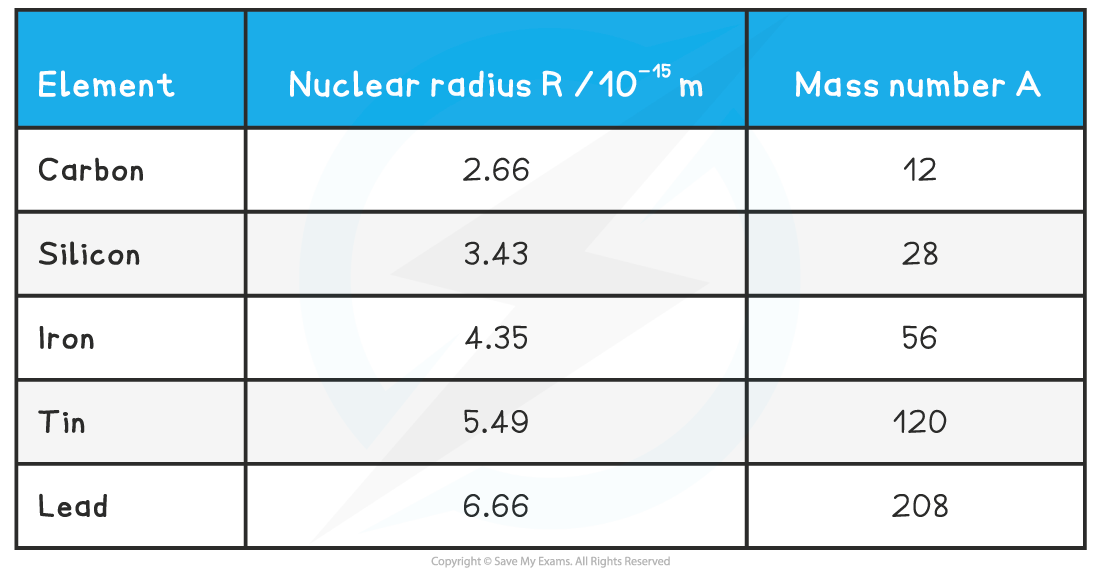
In general, nuclear radii are of the order 10–15 m or 1 fm
The nuclear radius, R, varies with nucleon number, A as follows:
The key features of this graph are:
The graph starts with a steep gradient at the origin
Then the gradient gradually decreases to almost horizontal
This means that
As more nucleons are added to a nucleus, the nucleus gets bigger
However, the number of nucleons A is not proportional to its size r
Calculating the Nuclear Radius
The radius of nuclei depends on the nucleon number, A of the atom
This makes sense because as more nucleons are added to a nucleus, more space is occupied by the nucleus, hence giving it a larger radius
The exact relationship between the radius and nucleon number can be determined from experimental data
By doing this, physicists were able to deduce the following relationship:
R = r0A1/3
Where:
R = nuclear radius (m)
A = nucleon / mass number
R0 = constant of proportionality = 1.2 fm = 1.2 x 10−15 m (the radius of a proton)
Mean Densities of Atoms and Nuclei
Equation for Nuclear Density
Assuming that the nucleus is spherical, its volume is equal to:
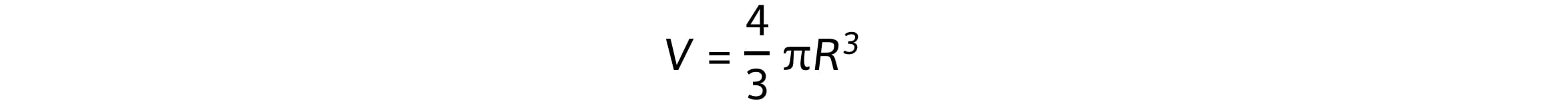
Where R is the nuclear radius, which is related to mass number, A, by the equation:
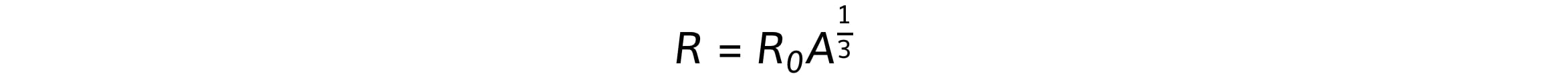
Where R0 is a constant of proportionality
Combining these equations gives:
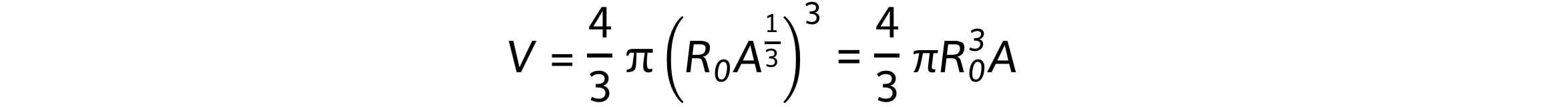
This shows that the nuclear volume, V, is proportional to the mass of the nucleus, A
Mass (m), volume (V), and density (ρ) are related by the equation:
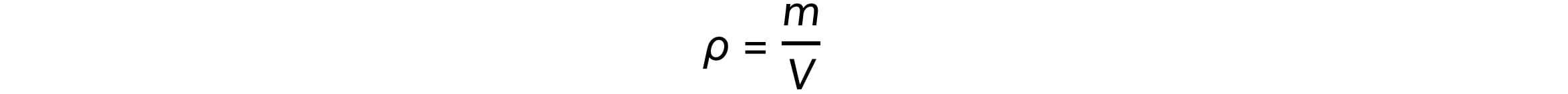
The mass, m, of a nucleus is equal to:
m = Au
Where:
A = the mass number
u = atomic mass unit
Using the equations for mass and volume, nuclear density is equal to:
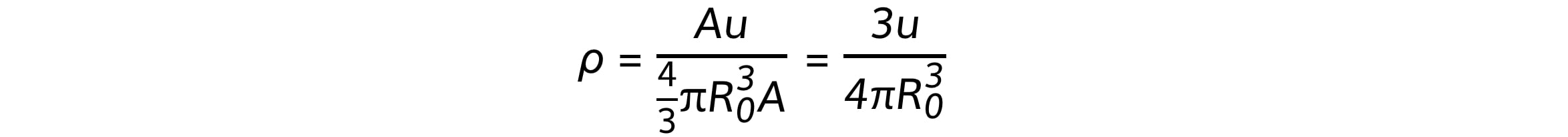
Since the mass number A cancels out, the remaining quantities in the equation are all constant
Therefore, this shows the density of the nucleus is:
Constant
Independent of the radius
The fact that nuclear density is constant shows that nucleons are evenly separated throughout the nucleus regardless of their size
Worked Example
Calculate the approximate density of a lithium nucleus.
Assume the atomic mass of lithium to be 7u.
Answer:
Step 1: Write down the equations:
Density:
Volume of a sphere:
From the data booklet: nuclear radius,
Where:
ro = constant = 1.2 x 10-15
A = mass number = 7 for lithium
Step 2: Combine equations:
V = π R3 = π (ro A1/3)3 = π ro3 A
Step 3: Calculate the volume of the nucleus:
V = πro3 A = π x (1.2 x 10-15)3 x 7 = 5.07 x 10-44 m3
Step 4: Calculate mass of lithium nucleus:
Mass = Au = 7 x (1.661 x 10-27) = 1.1627 x 10-26 kg
Step 5: Calculate the density:
Density = = = 2.29 x 1017 kg m-3
Step 6: Finalise your answer:
The density of a lithium nucleus is 2.3 x 1017 kg m-3 (2 s.f.)
Examiner Tips and Tricks
Don't let all the powers and letters confuse you. Work through each step of a question one by one. It is just mass/volume to get the density with a little bit of substitution!
Unlock more, it's free!
Join the 100,000+ Students that ❤️ Save My Exams
the (exam) results speak for themselves:
Was this revision note helpful?
Build on this topic
