Calculating Electric Potential (OCR A Level Physics) : Revision Note
Calculating Electric Potential
The electric potential in the field due to a point charge is defined as:
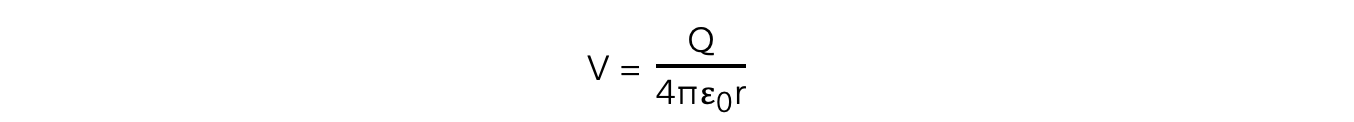
Where:
V = the electric potential (V)
Q = the point charge producing the potential (C)
ε0 = permittivity of free space (F m−1)
r = distance from the centre of the point charge (m)
This equation shows that for a positive (+) charge:
As the distance from the charge r decreases, the potential V increases
This is because more work has to be done on a positive test charge to overcome the repulsive force
For a negative (−) charge:
As the distance from the charge r decreases, the potential V decreases
This is because less work has to be done on a positive test charge since the attractive force will make it easier
The graph of potential V against distance r for a negative or positive charge is:

The electric potential around a positive charge decreases with distance and increases with distance around a negative charge
Unlike the gravitational potential equation, the minus sign in the electric potential equation will be included in the charge
The electric potential varies according to 1 / r
Note, this is different to electric field strength, which varies according to 1 / r2
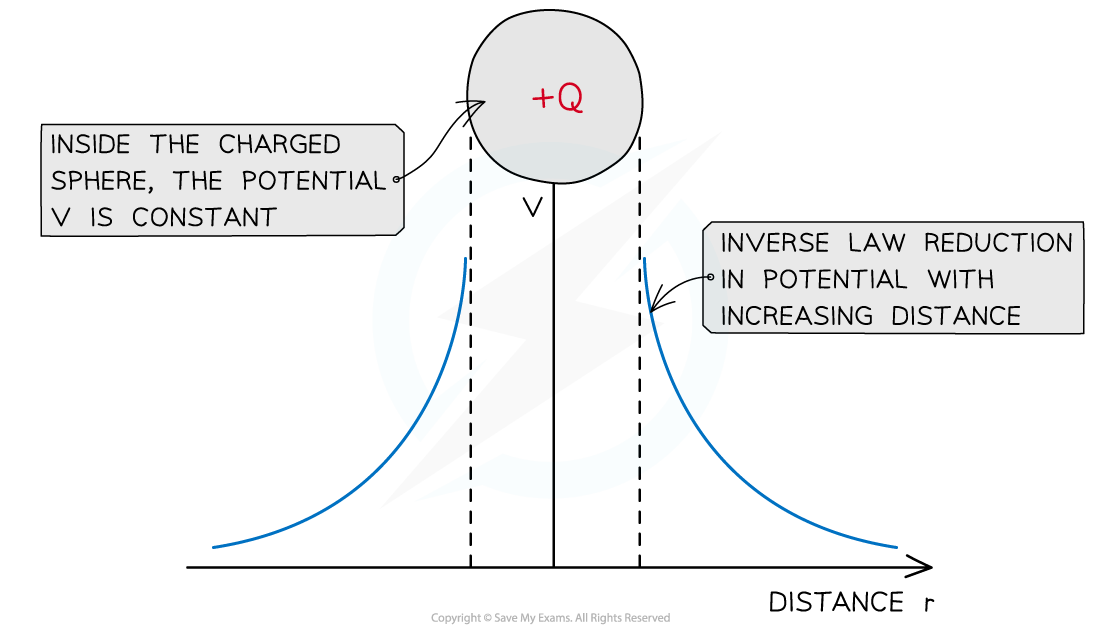
The potential changes as an inverse law with distance near a charged sphere
Note: this equation still applies to a conducting sphere. The charge on the sphere is treated as if it concentrated at a point in the sphere from the point charge approximation
Worked Example
A Van de Graaf generator has a spherical dome of radius 15 cm. It is charged up to a potential of 240 kV.
Calculate:
a) The charge stored on the dome
b) The potential at a distance of 30 cm from the dome
Answer:
Part (a)
Step 1: Write down the known quantities
Radius of the dome, r = 15 cm = 15 × 10−2 m
Potential difference, V = 240 kV = 240 × 103 V
Step 2: Write down the equation for the electric potential due to a point charge
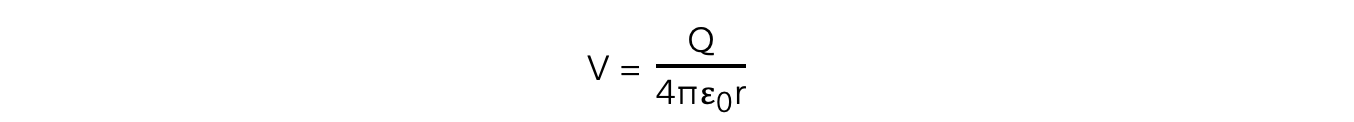
Step 3: Rearrange for charge Q
Q = V4πε0r
Step 4: Substitute in values
Q = (240 × 103) × (4π × 8.85 × 10−12) × (15 × 10−2)
Q = 4.0 × 10−6 C = 4.0 μC
Part (b)
Step 1: Write down the known quantities
Q = charge stored in the dome = 4.0 μC = 4.0 × 10−6 C
r = radius of the dome + distance from the dome = 15 + 30 = 45 cm = 45 × 10−2 m
Step 2: Write down the equation for electric potential due to a point charge
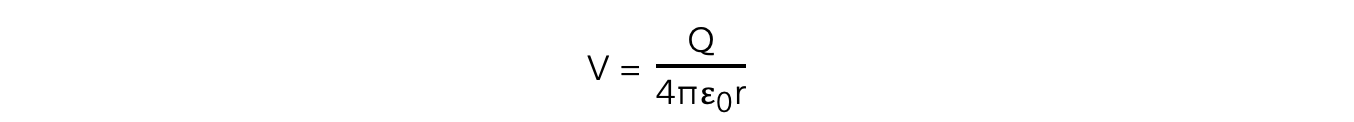
Step 3: Substitute in values and calculate final answer
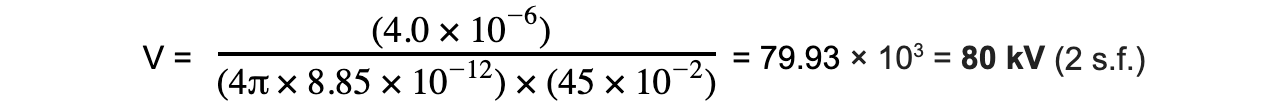

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
