Motion of Charged Particles in an E Field (OCR A Level Physics): Revision Note
Exam code: H556
Dielectric Action in a Parallel Plate Capacitor
Permittivity is the measure of how easy it is to generate an electric field in a certain material
The relativity permittivity εr is sometimes known as the dielectric constant
For a given material, it is defined as:
The ratio of the permittivity of a material to the permittivity of free space
This can be expressed as:
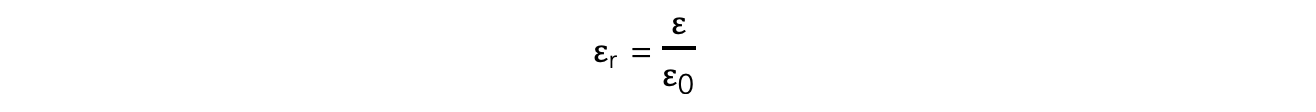
Where:
εr = relative permittivity
ε = permittivity of a material (F m−1)
ε0 = permittivity of free space (F m−1)
The relative permittivity has no units because it is a ratio of two values with the same unit
When the polar molecules in a dielectric align with the applied electric field from the plates, they each produce their own electric field
This electric field opposes the electric field from the plates
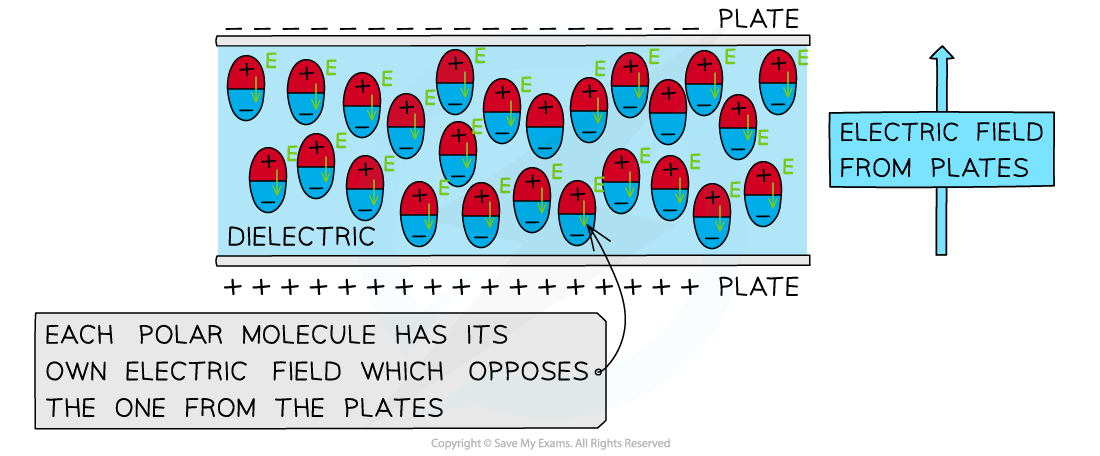
The electric field of the polar molecules opposes that of the electric field produced by the parallel plates
The larger the opposing electric field from the polar molecules in the dielectric, the larger the permittivity
In other words, the permittivity is how well the polar molecules in a dielectric align with an applied electric field
The opposing electric field reduces the overall electric field, which decreases the potential difference between the plates
Therefore, the capacitance of the plates increases
The capacitance of a capacitor can also be written in terms of the relative permittivity:

Where:
C = capacitance (F)
A = cross-sectional area of the plates (m2)
d = separation of the plates (m)
εr = relative permittivity of the dielectric between the plates
ε0 = permittivity of free space (F m−1)
Capacitor plates are generally square, therefore, if it has a length of L on all sides then the cross-sectional area will be A = L2
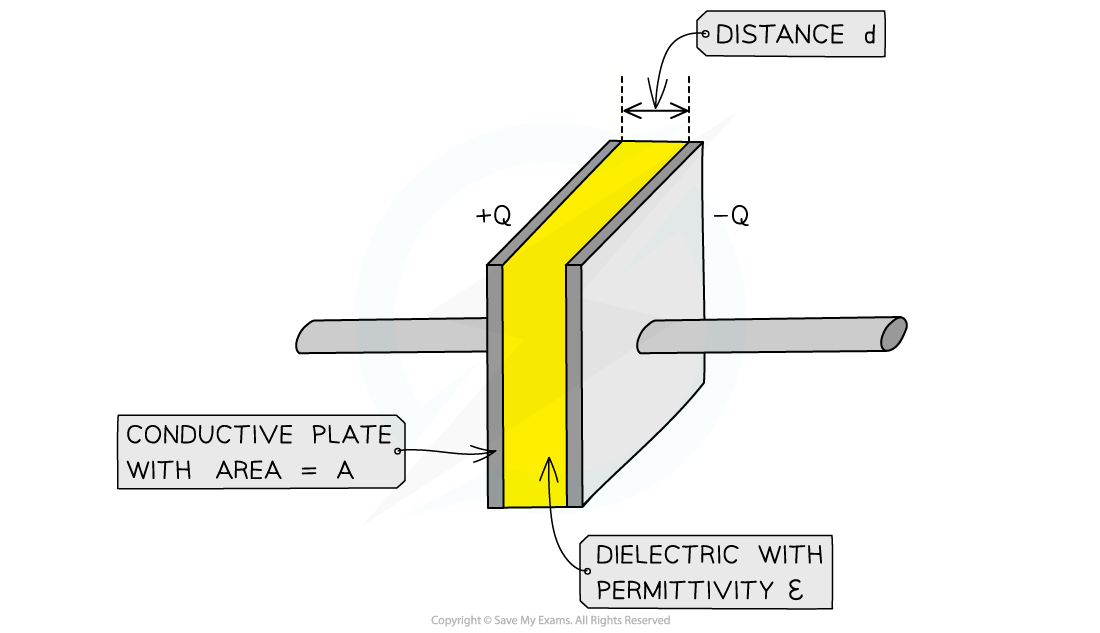
A parallel plate capacitor consists of conductive plates each with area A, a distance d apart and a dielectric ε between them
Worked Example
Calculate the permittivity of a material that has a relative permittivity of 4.5 × 1011.
State an appropriate unit for your answer.
Answer:
Step 1: Write down the relative permittivity equation
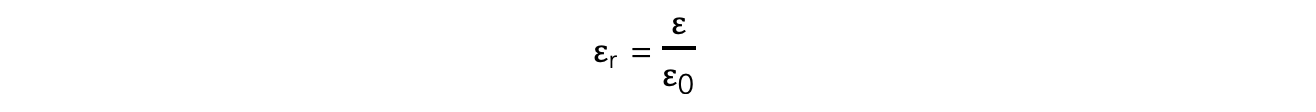
Step 2: Rearrange for permittivity of the material ε
ε = εrε0
Step 3: Substitute in the values
ε = (4.5 × 1011) × (8.85 × 10−12) = 3.9825 = 4 F m−1
Worked Example
A parallel-plate capacitor has square plates of length L separated by distance d and is filled with a dielectric. A second capacitor has square plates of length 3L separated by distance 3d and has air as its dielectric.
Both capacitors have the same capacitance.
Determine the relative permittivity of the dielectric in the first capacitor.
Answer:

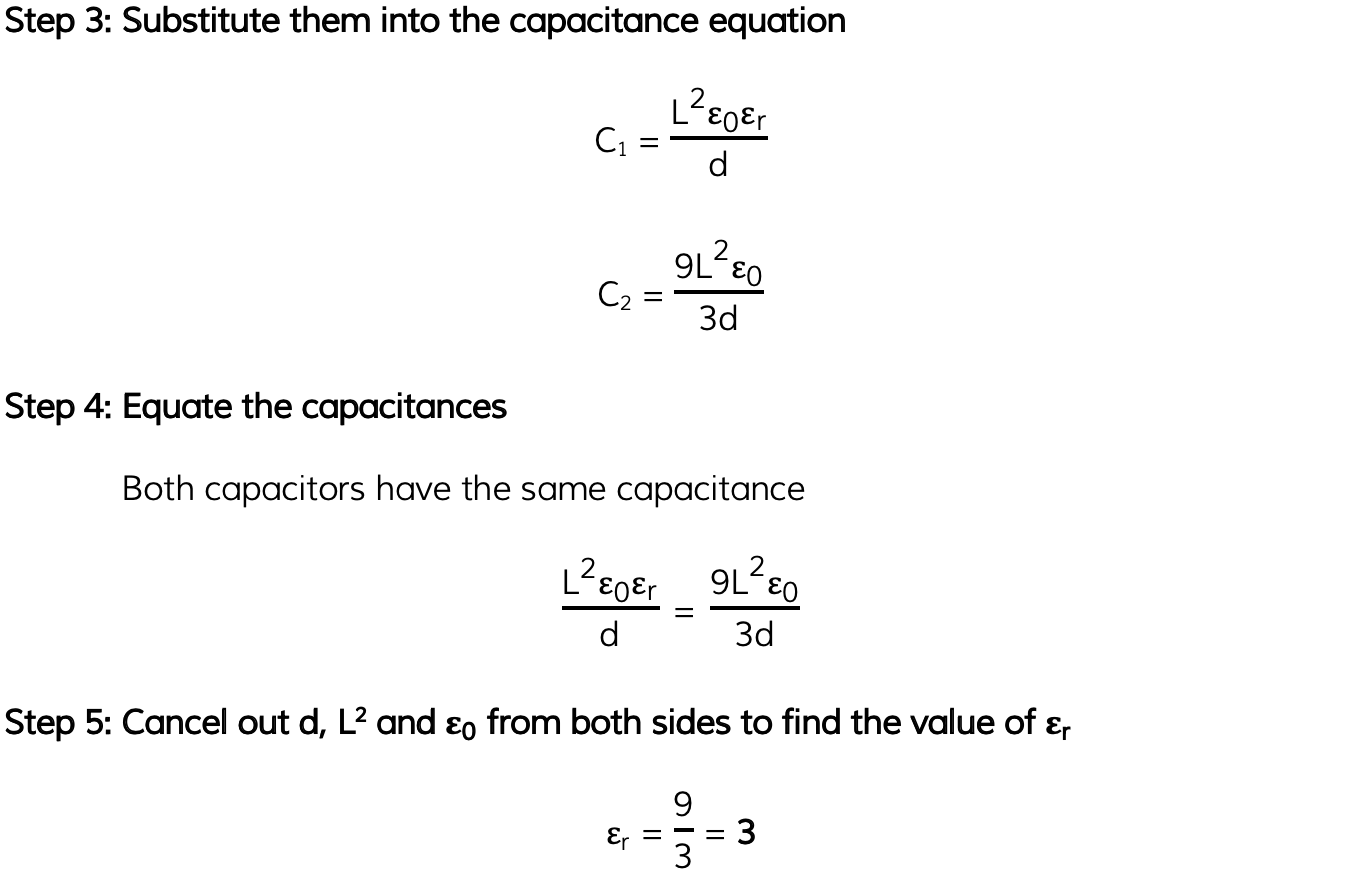
Examiner Tips and Tricks
Remember that A, the cross-sectional area, is only for one of the parallel plates. Don't multiply this by 2 for both the plates for the capacitance equation!
Motion of Charged Particles in an Electric Field
A charged particle in an electric field will experience a force on it that will cause it to move
If a charged particle remains still in a uniform electric field
It will move parallel to the electric field lines (along or against the field lines depending on its charge)
If a charged particle in motion travels initially perpendicular through a uniform electric field (e.g. between two charged parallel plates)
It will experience a constant electric force and travel in a parabolic trajectory
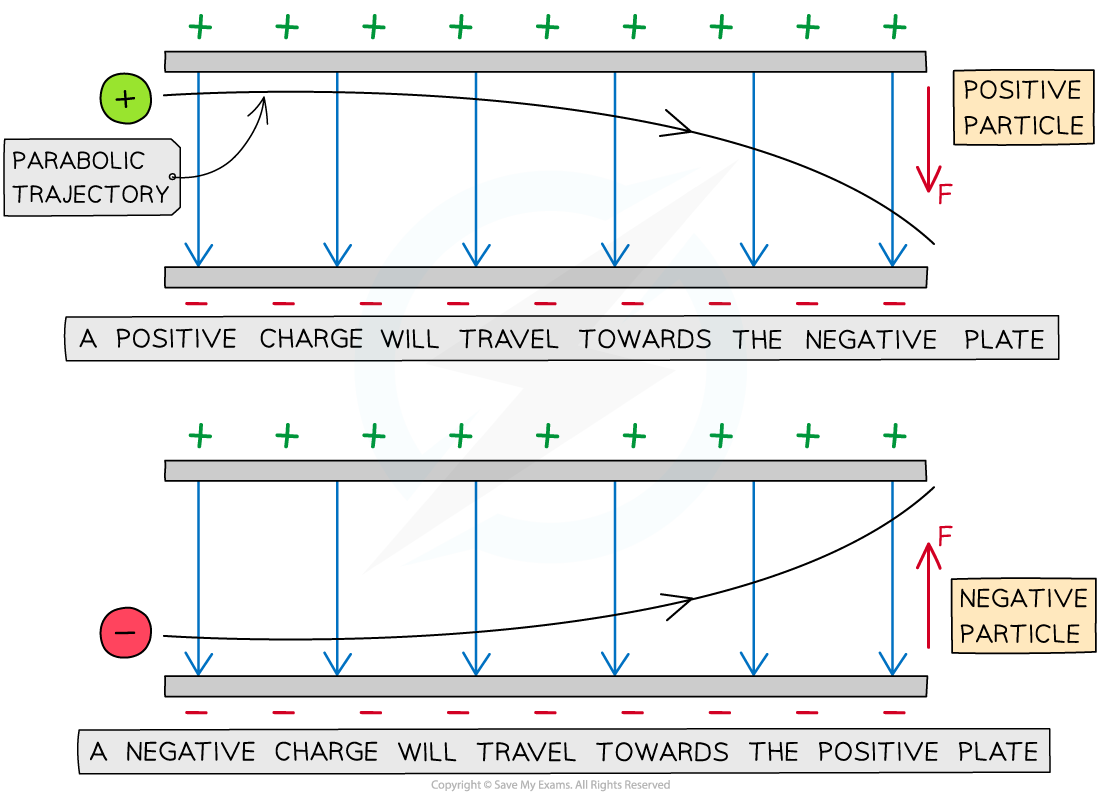
The parabolic path of charged particles in a uniform electric field
The direction of the parabola will depend on the charge of the particle
A positive charge will be deflected towards the negative plate
A negative charge will be deflected towards the positive plate
The force on the particle is the same at all points and is always in the same direction
Note: an uncharged particle, such as a neutron experiences no force in an electric field and will therefore travel straight through the plates undeflected
The amount of deflection depends on the following properties of the particles:
Mass – the greater the mass, the smaller the deflection and vice versa
Charge – the greater the magnitude of the charge of the particle, the greater the deflection and vice versa
Speed – the greater the speed of the particle, the smaller the deflection and vice versa
Worked Example
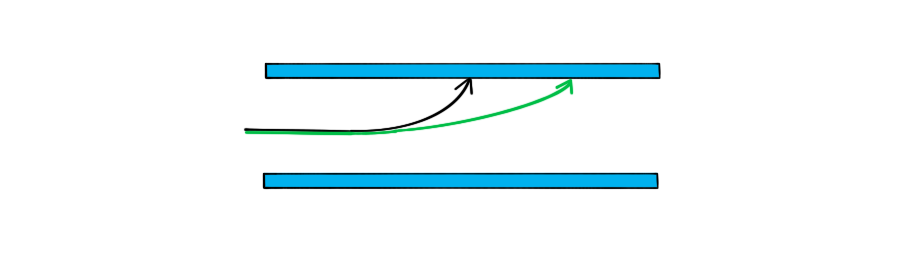
A single proton travelling with a constant horizontal velocity enters a uniform electric field between two parallel charged plates. The diagram shows the path taken by the proton.

Draw the path taken by a boron nucleus that enters the electric field at the same point and with the same velocity as the proton.
Atomic number of boron = 5
Mass number of boron = 11
Answer:
Step 1: Compare the charge of the boron nucleus to the proton
Boron has 5 protons, meaning it has a charge 5 × greater than the proton
The force on boron will therefore be 5 × greater than on the proton
Step 2: Compare the mass of the boron nucleus to the proton
The boron nucleus has a mass of 11 nucleons meaning its mass is 11 × greater than the proton
The boron nucleus will therefore be less deflected than the proton
Step 3: Draw the trajectory of the boron nucleus
Since the mass comparison is much greater than the charge comparison, the boron nucleus will be much less deflected than the proton
The nucleus is positively charged since the neutrons in the nucleus have no charge
Therefore, the shape of the path will be the same as the proton

Unlock more, it's free!
Did this page help you?