Electric Field Strength of a Point Charge (OCR A Level Physics)

• The electric field strength describes how strong or weak an electric field is at that point
• A point charge produces a radial field
  • A charge sphered also acts like a point charge

• The electric field strength E at a distance r due to a point charge Q in free space is defined by:

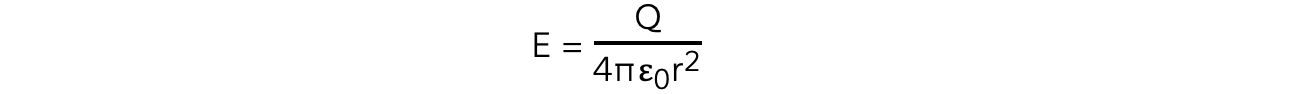
• Where:
  • Q = the point charge producing the radial electric field (C)
  • r = distance from the centre of the charge (m)
  • ε₀ = permittivity of free space (F m⁻¹)

• This equation shows:
  • Electric field strength in a radial field is not constant
  • As the distance from the charge r increases, E decreases by a factor of 1/r²

• This is an inverse square law relationship with distance
  • This means the field strength E decreases by a factor of four when the distance r is doubled

• Note: this equation is only for the field strength around a point charge since it produces a radial field

 

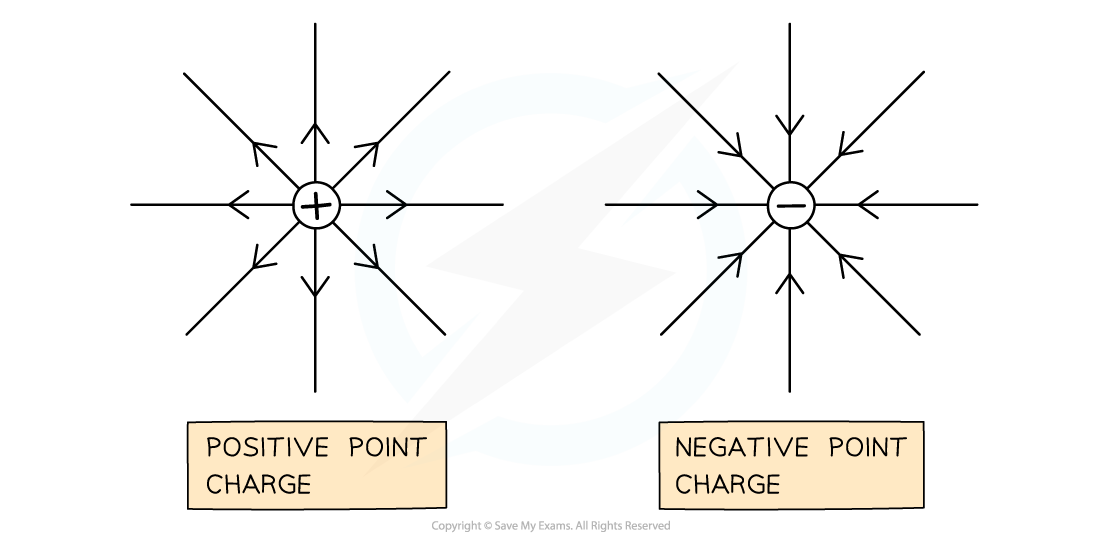
Direction of positive and negative point charges

• The electric field strength is a vector Its direction is the same as the electric field lines
  • If the charge is negative, the E field strength is negative and points towards the centre of the charge
  • If the charge is positive, the E field strength is positive and points away from the centre of the charge

• This equation is analogous to the gravitational field strength around a point mass

Step 1: Write down the known values

• • Electric field strength, E = 1.5 × 10⁵ V m^-1
  • Radius of sphere, r = 15 / 2 = 7.5 cm = 7.5 × 10^-2 m

Step 2: Write out the equation for electric field strength

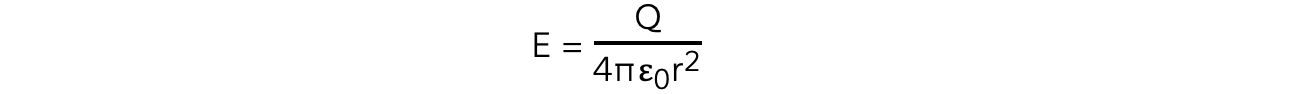
Step 3: Rearrange for charge Q

Q = 4πε₀Er²

Step 4: Substitute in values

Q = (4π × 8.85 × 10⁻¹²) × (1.5 × 10⁵) × (7.5 × 10⁻²)²

Q = 9.38 × 10⁻⁸ C = 94 nC (2 s.f.)