Capacitor Charge & Discharge (OCR A Level Physics)

Charging & Discharging

Charging

• Capacitors are charged by a power supply (e.g. a battery)

• When charging, the electrons are pulled from the plate connected to the positive terminal of the power supply

  • Hence the plate nearest the positive terminal is positively charged

• They travel around the circuit and are pushed onto the plate connected to the negative terminal

  • Hence the plate nearest the negative terminal is negatively charged

• As the negative charge builds up, fewer electrons are pushed onto the plate due to electrostatic repulsion from the electrons already on the plate

• When no more electrons can be pushed onto the negative plate, the charging stops

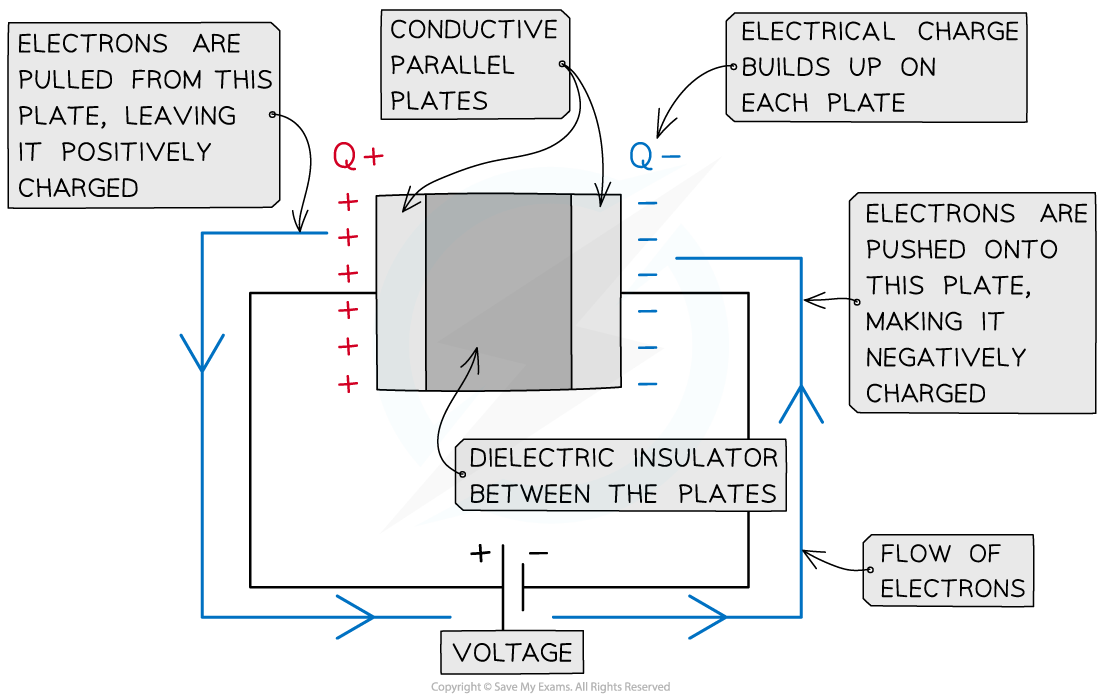
A parallel plate capacitor is made up of two conductive plates with opposite charges building up on each plate

• At the start of charging, the current is large and gradually falls to zero as the electrons stop flowing through the circuit

  • The current decreases exponentially

  • This means the rate at which the current decreases is proportional to the amount of current it has left

• Since an equal but opposite charge builds up on each plate, the potential difference between the plates slowly increases until it is the same as that of the power supply

• Similarly, the charge of the plates slowly increases until it is at its maximum charge defined by the capacitance of the capacitor

Graphs of variation of current, p.d. and charge with time for a capacitor charging through a battery

• The key features of the charging graphs are:

  • The shapes of the p.d. and charge against time graphs are identical

  • The current against time graph is an exponential decay curve

  • The initial value of the current starts on the y axis and decreases exponentially

  • The initial value of the p.d. and charge starts at 0 up to a maximum value

Discharging

• Capacitors are discharged through a resistor with no power supply present

• The electrons now flow back from the negative plate to the positive plate until there are equal numbers on each plate and no potential difference between them

• Charging and discharging is commonly achieved by moving a switch that connects the capacitor between a power supply and a resistor

The capacitor charges when connected to terminal P and discharges when connected to terminal Q

• At the start of discharge, the current is large (but in the opposite direction to when it was charging) and gradually falls to zero

• As a capacitor discharges, the current, p.d. and charge all decrease exponentially

  • This means the rate at which the current, p.d. or charge decreases is proportional to the amount of current, p.d or charge it has left

• The graphs of the variation with time of current, p.d. and charge are all identical and follow a pattern of exponential decay

Graphs of variation of current, p.d and charge with time for a capacitor discharging through a resistor

• The key features of the discharge graphs are:

  • The shape of the current, p.d. and charge against time graphs are identical

  • Each graph shows exponential decay curves with decreasing gradient

  • The initial values (typically called I₀, V₀ and Q₀ respectively) start on the y axis and decrease exponentially

• The rate at which a capacitor discharges depends on the resistance of the circuit

  • If the resistance is high, the current will decrease and charge will flow from the capacitor plates more slowly, meaning the capacitor will take longer to discharge

  • If the resistance is low, the current will increase and charge will flow from the capacitor plates quickly, meaning the capacitor will discharge faster

Investigating the Charge & Discharge of a Capacitor

Aim of the Experiment

• The overall aim of this experiment is to calculate the capacitance of a capacitor. This is just one example of how this required practical might be carried out

Variables

• Independent variable = time, t 

• Dependent variable = potential difference, V

• Control variables:

  • Resistance of the resistor

  • Current in the circuit

Equipment List

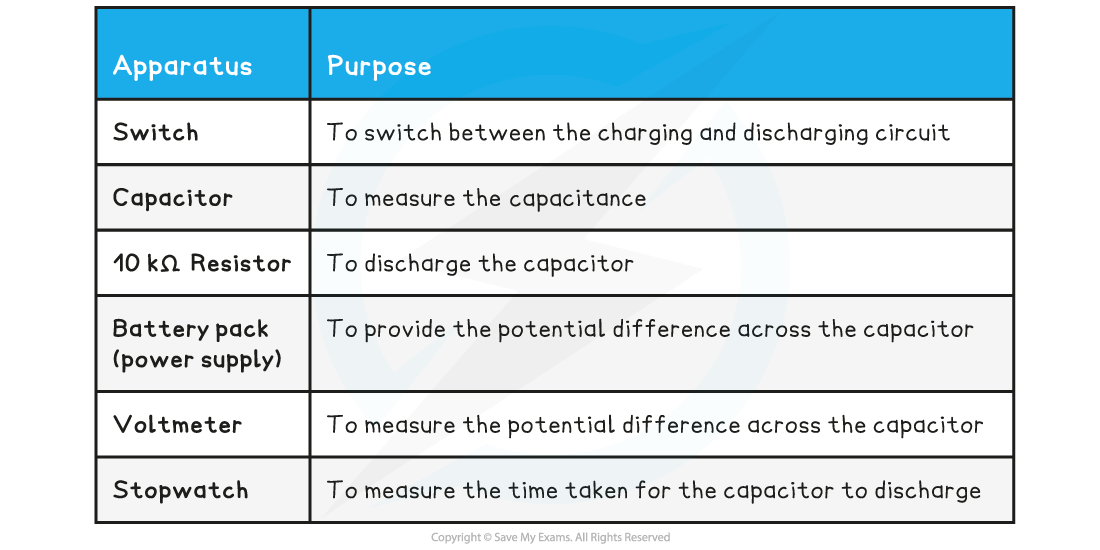
• Resolution of measuring equipment:

  • Voltmeter = 0.1 V

  • Stopwatch = 0.01 s

Method

1. Set up the apparatus like the circuit above, making sure the switch is not connected to X or Y (no current should be flowing through)

2. Set the battery pack to a potential difference of 10 V and use a 10 kΩ resistor

   • Note: The capacitor should initially be fully discharged

3. Charge the capacitor fully by placing the switch at point X

   • The voltmeter reading should read the same voltage as the battery (10 V)

4. Move the switch to point Y

5. Record the voltage reading every 10 s down to a value of 0 V. A total of 8-10 readings should be taken

• An example table might look like this:

Analysing the Results

• The potential difference (p.d.) across the capacitance is defined by the equation:

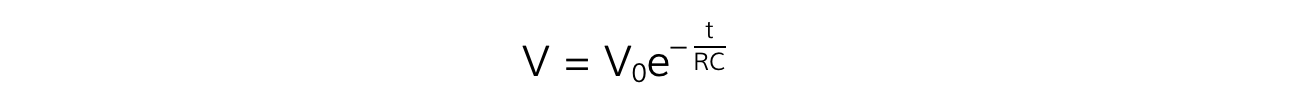
• Where:

  • V = p.d. across the capacitor (V)

  • V₀ = initial p.d across the capacitor (V)

  • t = time (s)

  • e = exponential function

  • R = resistance of the resistor (Ω)

  • C = capacitance of the capacitor (F)

• Rearranging this equation for ln(V) by taking the natural log (ln) of both sides:

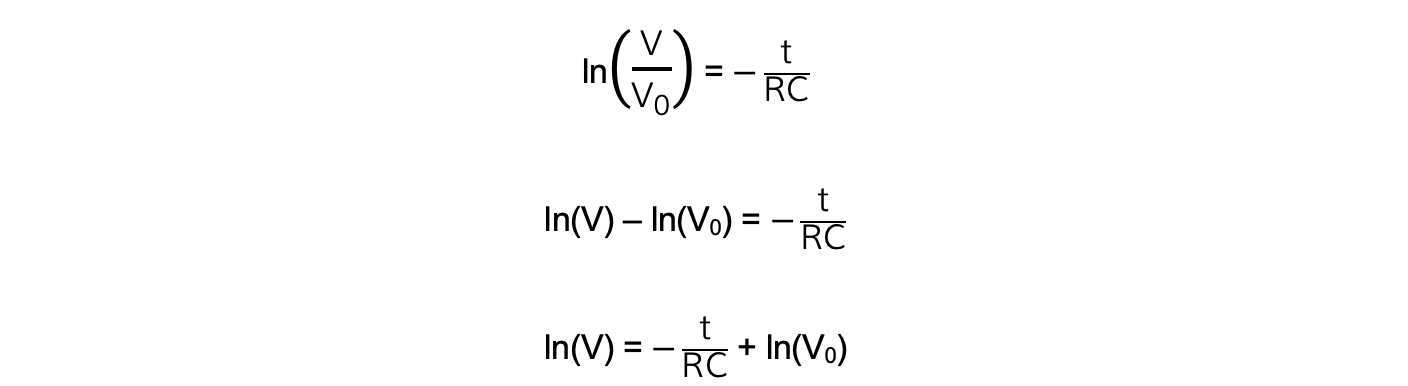
• Comparing this to the equation of a straight line: y = mx + c

  • y = ln(V)

  • x = t

  • gradient = -1/RC

  • c = ln(V₀)

1. Plot a graph of ln(V) against t and draw a line of best fit

2. Calculate the gradient (this should be negative)

3. The capacitance of the capacitor is equal to:

   

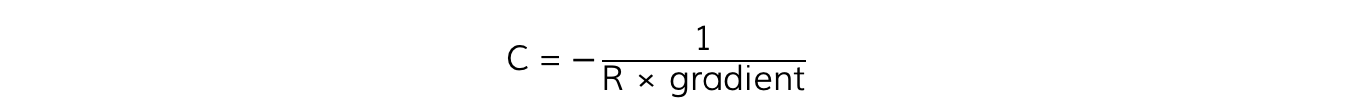
Evaluating the Experiment

Systematic Errors:

• If a digital voltmeter is used, wait until the reading is settled on a value if it is switching between two

• If an analogue voltmeter is used, reduce parallax error by reading the p.d. at eye level to the meter

• Make sure the voltmeter starts at zero to avoid a zero error

Random Errors:

• Use a resistor with a large resistance so the capacitor discharges slowly enough for the time to be taken accurately at p.d. intervals

• Using a datalogger will provide more accurate results for the p.d. at a certain time. This will reduce the error in the speed of the reflex needed to stop the stopwatch at a certain p.d.

• The experiment could be repeated by measuring the time for the capacitor to charge instead

Safety Considerations

• Keep water or any fluids away from the electrical equipment

• Make sure no wires or connections are damaged

• Ensure use of appropriate fuses to avoid a short circuit or a fire

• Using a resistor with too low a resistance will not only mean the capacitor discharges too quickly, but also that the wires will become very hot due to the high current

  • This will affect the result and introduce a safety hazard

• Capacitors can still retain charge after power is removed which could cause an electric shock

  • These should be fully discharged and removed after a few minutes