Revision NotesExam QuestionsPast Papers
A LevelPhysicsOCRRevision Notes6. Particles & Medical PhysicsUltrasoundDoppler Effect in Ultrasound

Doppler Effect in Ultrasound (OCR A Level Physics)

Revision Note

Katie M

Author

Katie M

Last updated

Doppler Effect in Ultrasound

  • The Doppler effect is defined as:

    The frequency change of a wave due to the relative motion between a source and an observer

  • When the source starts to move towards the observer, the wavelength of the waves is shortened

    • The sound therefore appears at a higher frequency to the observer

  • The frequency is increased when the source is moving towards the observer

  • The frequency is decreased when the source is moving away from the observer

    • This applies to ultrasound in the exact same way as it does to sound waves

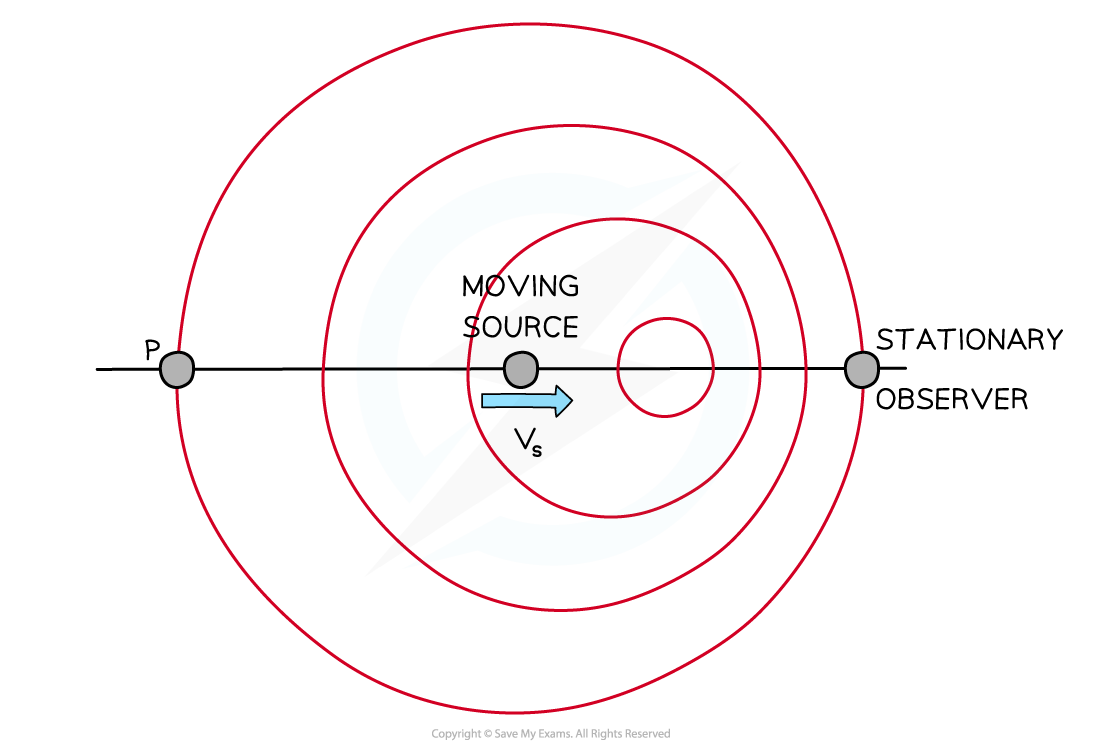
Doppler shift diagram 2, downloadable AS & A Level Physics revision notes

Doppler effect of a moving source and stationary observer

  • For a wave of frequency, f0, that reflects at a moving boundary, the new frequency, fr, of the reflected pulse is given by:

f subscript r space equals space f subscript 0 space open parentheses fraction numerator c over denominator c minus 2 v end fraction close parentheses

  • Where:

    • f0 = frequency of original wave (Hz)

    • fr = frequency of reflected wave (Hz)

    • v = velocity of the moving boundary (m s−1)

    • c = velocity of the wave (m s−1)

  • The factor of 2 appears due to the wave travelling to the boundary and back again

  • In medicine, Doppler imaging can be used as a non-invasive technique to measure the speed of blood flow in the heart or in an artery

    • This is effective because blood contains iron which is very reflective

  • The journey of the ultrasound is as follows:

    • Pulses of ultrasound are emitted from a transducer into a blood vessel

    • The ultrasound pulses are reflected by moving blood cells

    • The moving blood causes a shift in the frequency of the ultrasound

    • The transducer detects an increase in frequency if the blood is moving towards the transducer and a decrease if it is moving away

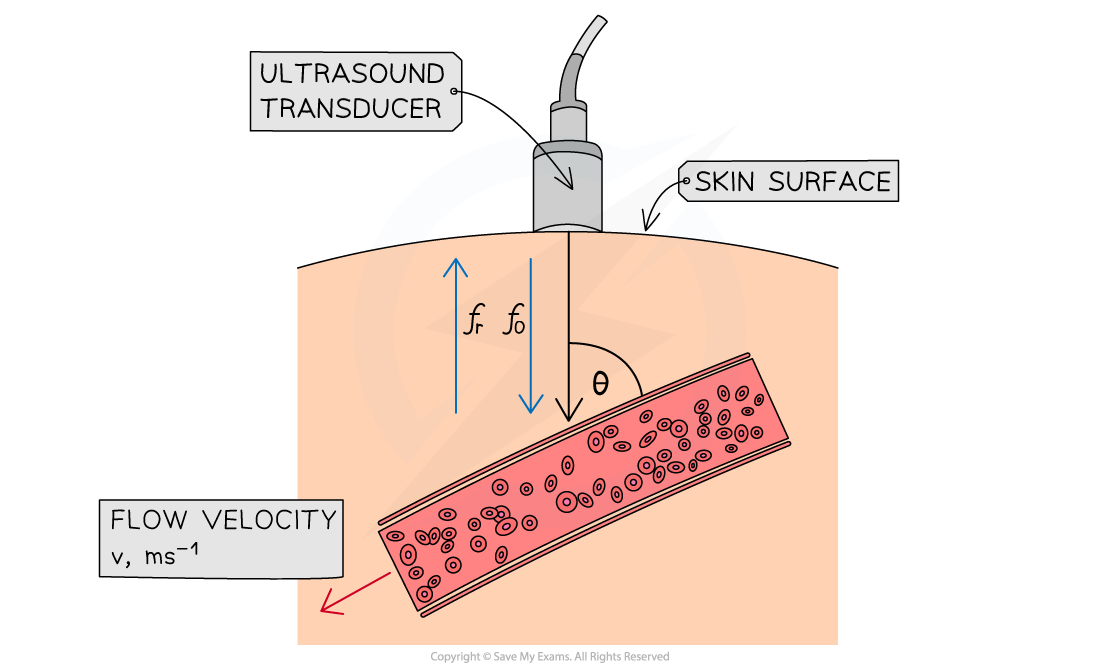
6-13-5-ultrasound-doppler-imaging_ocr-al-physics

  • This frequency shift, Δf, can be calculated using the equation:

increment f equals f subscript 0 minus f subscript r equals fraction numerator 2 f subscript 0 v space cos space theta over denominator c end fraction

  • Where:

    • f0 = frequency of ultrasound emitted by the transducer (Hz)

    • fr = frequency of ultrasound received by the transducer (Hz)

    • Δf = difference between emitted and received frequencies (Hz)

    • v = velocity of the blood (m s−1)

    • c = velocity of ultrasound in blood (m s−1)

    • θ = angle between the transducer and the blood vessel (°)

  • This can be rearranged to give:

fraction numerator increment f over denominator f subscript 0 end fraction equals fraction numerator 2 v space cos space theta over denominator c end fraction

Worked Example

A patient is undergoing diagnostic tests to determine the cause of an underlying heart condition. Blood flow tests are done on the patient's aorta using ultrasound imaging. 

Ultrasound of frequency 8.5 MHz is transmitted from a transducer through the skin into the aorta. The reflected frequency is found to be 8.495 MHz. The angle the transducer makes with the skin is 15°.

The velocity of sound in blood is 1570 m s−1 and the aorta has an internal diameter of 30 mm.

Calculate:

a) The speed of the blood flow in the aorta.

b) The volume of blood, in cm3, moving past any point in 1 s.

Answer:

Part (a)

Step 1: List the known quantities

  • Transmitted frequency of the ultrasound, f0 = 8.5 MHz

  • Reflected frequency of the ultrasound, fr = 8.495 MHz

  • Change in frequency, Δf = 8.5 − 8.495 = 0.005 MHz

  • Velocity of sound in blood, c = 1570 m s−1

  • Angle between the transducer and skin, θ = 15°

Step 2: Write out the equation for Doppler shift of ultrasound

fraction numerator increment f over denominator f subscript 0 end fraction equals fraction numerator 2 v space cos space theta over denominator c end fraction

Step 3: Rearrange for the speed, v, and calculate

v equals fraction numerator c over denominator 2 cos space theta end fraction open parentheses fraction numerator increment f over denominator f subscript 0 end fraction close parentheses equals fraction numerator c increment f over denominator 2 f subscript 0 space cos space theta end fraction

v equals fraction numerator 1570 cross times open parentheses 0.005 cross times 10 to the power of 6 close parentheses over denominator 2 open parentheses 8.5 cross times 10 to the power of 6 close parentheses space cos space 15 end fraction= 0.478

v = 0.48 m s−1

Part (b)

Step 1: List the known quantities

  • Radius of the aorta, r = 15 mm = 1.5 cm

  • Blood flow rate, v = 0.48 m s−1 = 48 cm s−1

Step 2: Calculate the cross-sectional area of the aorta

  • Cross-sectional area = πr2 = π(1.5)2 = 7.1 cm2

Step 3: Determine the volume of blood passing through the aorta each second

  • Volume flow rate = cross-sectional area (cm2) × blood flow rate (cm s−1)

  • Volume flow rate = 7.1 × 48 = 341 cm3 s−1

Step 4: State the volume of blood in 1 s

  • The volume of blood that flows in 1 s = 341 cm3 

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:Reflection of Ultrasound
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.