Acoustic Impedance (OCR A Level Physics) : Revision Note
Acoustic Impedance
The acoustic impedance, Z, of a medium is defined as:
The product of the speed of the ultrasound in the medium and the density of the medium
This quantity describes how much resistance an ultrasound beam encounters as it passes through a tissue
Acoustic impedance can be calculated using the equation:
Z = ρc
Where:
Z = acoustic impedance (kg m-2 s-1)
ρ = the density of the material (kg m-3)
c = the speed of sound in the material (m s-1)
This equation shows:
The higher the density of a tissue, the greater the acoustic impedance
The faster the ultrasound travels through the material, the greater the acoustic impedance also
This is because sound travels faster in denser materials
Sound is fastest in solids and slowest in gases
The closer the particles in the material, the faster the vibrations can move through the material
At the boundary between media of different acoustic impedances, some of the wave energy is reflected and some is transmitted
The greater the difference in acoustic impedance between the two media, the greater the reflection and the smaller the transmission
Two materials with the same acoustic impedance would give no reflection
Two materials with a large difference in values would give much larger reflections
Air has an acoustic impedance of Zair = 400 kg m-2 s-1
Skin has an acoustic impedance of Zskin = 1.7 × 106 kg m-2 s-1
The large difference means ultrasound would be significantly reflected, hence a coupling gel is necessary
The coupling gel used has a similar Z value to skin, meaning that very little ultrasound is reflected
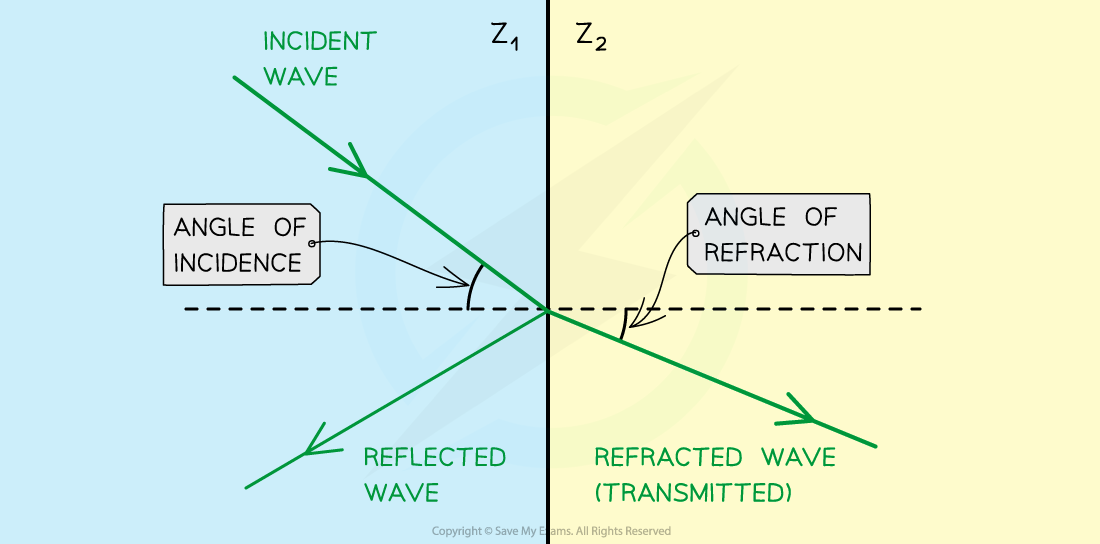
Refraction and reflection of ultrasound waves at a boundary between two materials with different acoustic impedances (in this case, Z1 < Z2 )
Worked Example
The table shows the speed of sound acoustic impedance in four different materials.

Use the table to calculate the value for the density of bone.
Answer:
Step 1: Write down known quantities
Acoustic impedance of bone, Z = 7.0 × 106 kg m-2 s-1
Speed of ultrasound in bone, c = 4100 m s-1
Step 2: Write out the equation for acoustic impedance
Z = ρc
Step 3: Rearrange for density and calculate
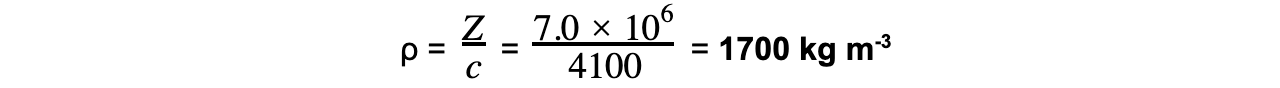
Examiner Tips and Tricks
A common mistake is to confuse the c in the acoustic impedance equation for the speed of light - don’t do this!
Impedance Matching in Ultrasound Scans
The intensity reflection coefficient α is defined as:
The ratio of the intensity of the reflected wave relative to the incident (transmitted) wave
This can be calculated using the fraction:
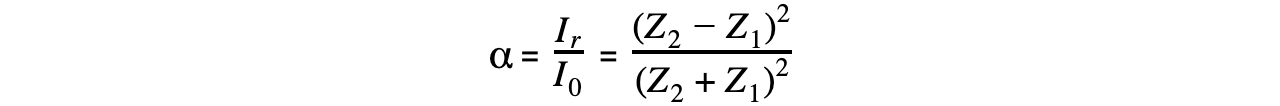
Where:
α = intensity reflection coefficient
IR = intensity of the reflected wave (W m-2)
I0 = intensity of the incident wave (W m-2)
Z1 = acoustic impedance of one material (kg m-2 s-1)
Z2 = acoustic impedance of a second material (kg m-2 s-1)
This ratio shows:
If there is a large difference between the impedance of the two materials, then most of the energy will be reflected
If the impedance is the same, then there will be no reflection
Coupling Medium
When ultrasound is used in medical imaging, a coupler is needed between the transducer and the body
This is because the soft tissues of the body are much denser than air
If air is present between the transducer and the body, then almost all the ultrasound energy will be reflected
To counter this, a coupling gel is placed between the transducer and the body
This is because skin and coupling gel have a similar density, so little ultrasound is reflected
This is an example of impedance matching, which is defined as when:
Two media have a similar acoustic impedance, resulting in little to no reflection of the ultrasound wave
In terms of intensity reflection coefficient, α, between the two media:
At lower values of α, the media are impedance matched, so less reflection occurs
At higher values of α, the media are not impedance matched, so more reflection occurs
Worked Example
A beam of ultrasound is incident at right-angles to a boundary between two materials, as shown in the diagram.
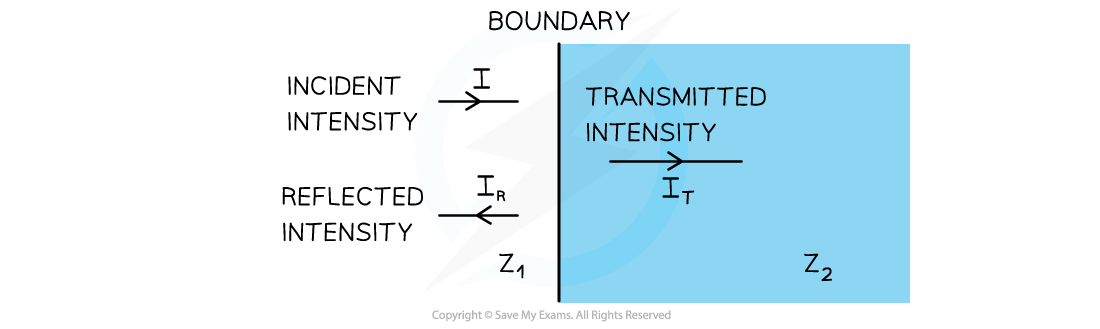
The materials have acoustic impedances of Z1 and Z2. The intensity of the transmitted ultrasound beam is IT, and the reflected intensity is IR.

a) State the relationship between I, IT and IR.
b) Use the data from the table to determine the reflection coefficient, α, for a boundary between
(i) Gel and soft tissue
(ii) Air and soft tissue
c) Explain why gel is usually put on the skin during medical diagnosis using ultrasound.
Answer:
Part (a)
Step 1: List the known quantities
Intensity of incident wave = I
Intensity of the transmitted wave = IT
Intensity of the reflected wave = IR
Step 2: Relate the quantities:
The incident intensity is equal to the sum of the transmitted and reflected intensities:
Incident intensity = Transmitted intensity + Reflected intensity
I = IT + IR
Part (b)(i)
Step 1: List the known quantities
Acoustic impedance of gel, Z1 = 1.5 × 106 kg m-2 s-1
Acoustic impedance of soft tissue, Z2 = 1.6 × 106 kg m-2 s-1
Step 2: Write down the equation for intensity reflection coefficient α
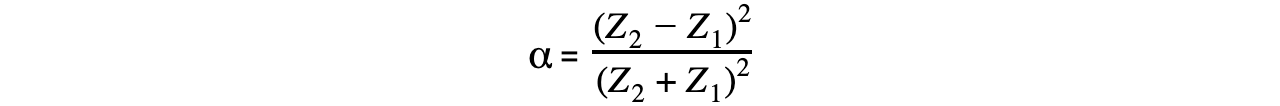
Step 3: Calculate the intensity reflection coefficient
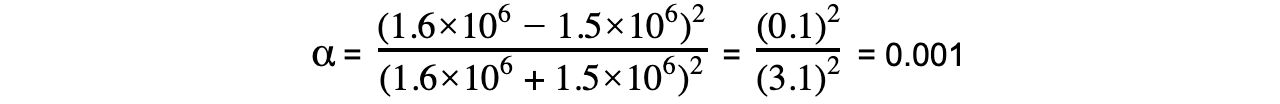
This result means that only 0.1% of the incident intensity will be reflected, with the remaining being transmitted
Part (b)(ii)
Step 1: List the known quantities
Air, Z1 = 4.3 × 102 kg m-2 s-1
Soft tissue, Z2 = 1.6 × 106 kg m-2 s-1
Step 2: Calculate the intensity reflection coefficient
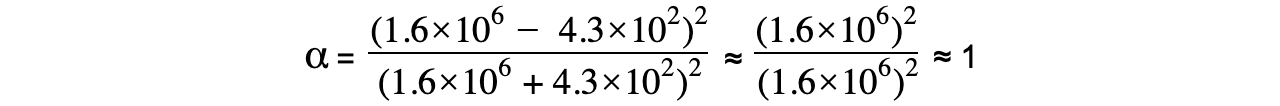
This result means that 100% of the incident intensity will be reflected, with none being transmitted
Part (c)
Why gel is usually put on the skin during medical diagnosis using ultrasound
At the air-soft tissue boundary, the intensity reflection coefficient is α ≈ 1
Therefore, without gel, there is almost complete reflection - no ultrasound is transmitted through the skin
At the gel-soft tissue boundary, the intensity reflection coefficient is α = 0.001
Therefore, the gel enables almost complete transmission of the ultrasound through the skin, with very little reflection

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
