PET Scans (OCR A Level Physics): Revision Note

Positron Emission Tomography (PET) Scanning

• Positron Emission Tomography (PET) is defined as:

  A type of nuclear medical procedure that images tissues and organs by measuring the metabolic activity of the cells of body tissues

• In PET scanning, a beta-plus emitting radioactive tracer is used in order to stimulate positron-electron annihilation to produce gamma photons

  • These are then detected using a ring of gamma cameras

Principles of PET Scanning

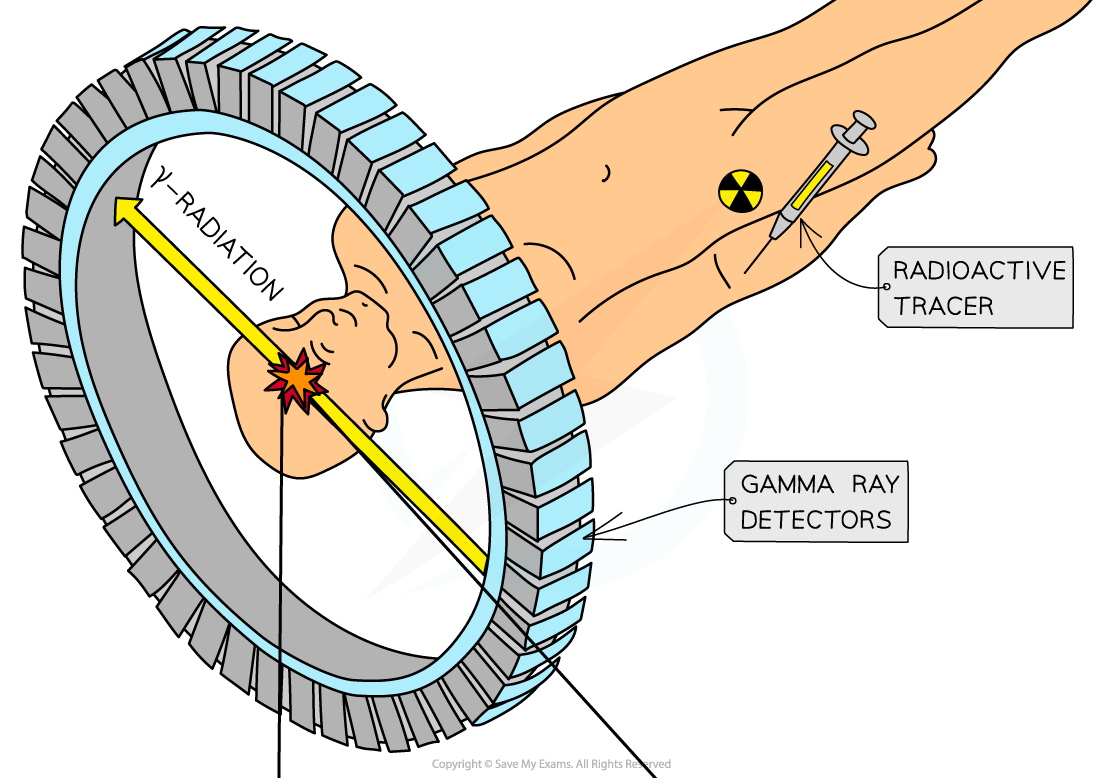
Before the scan

• The patient is injected with a beta-plus emitting isotope, usually fluorine-18 (F-18)

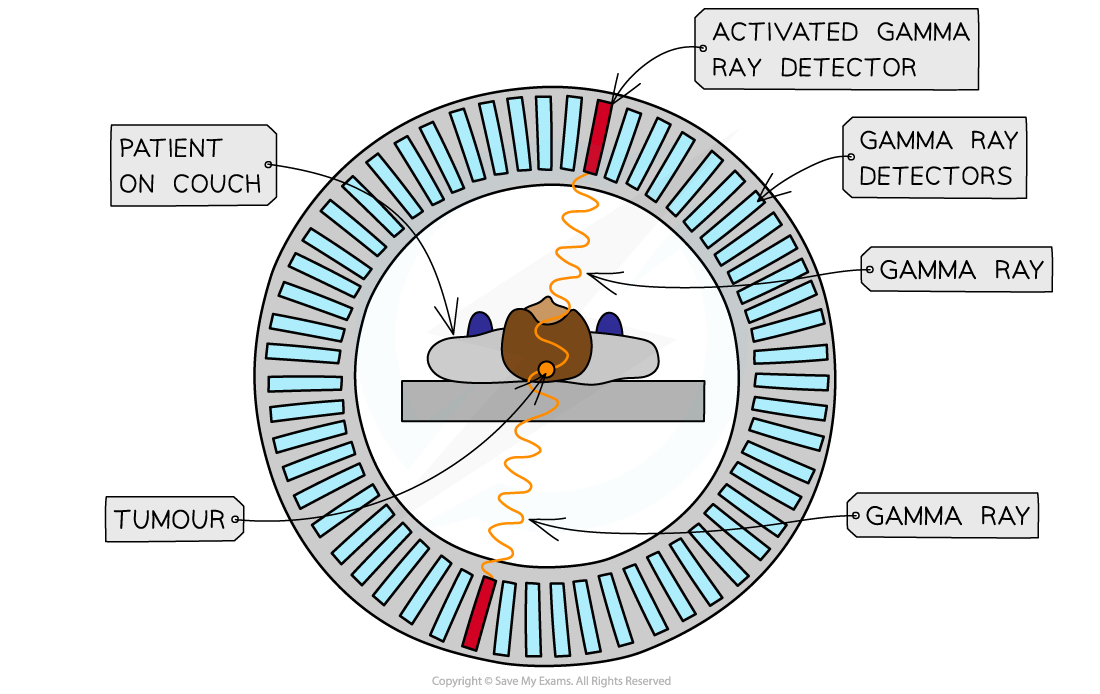
During the scan

• The part of the body being studied is surrounded by a ring of gamma cameras

• The positrons from the F-18 nuclei annihilate with electrons in the patient

• The annihilation of a positron and an electron produces two identical gamma photons travelling in opposite directions

• The delay time between these two gamma ray photons is used to determine the location of the annihilation due to the F-18 tracer

  • Photons that do not arrive within a nanosecond of each other are ignored, since they cannot have come from the same point

After the scan

• Computer connected to the gamma cameras detect the signal and an image is formed by the computer

Detecting gamma rays with a PET scanner

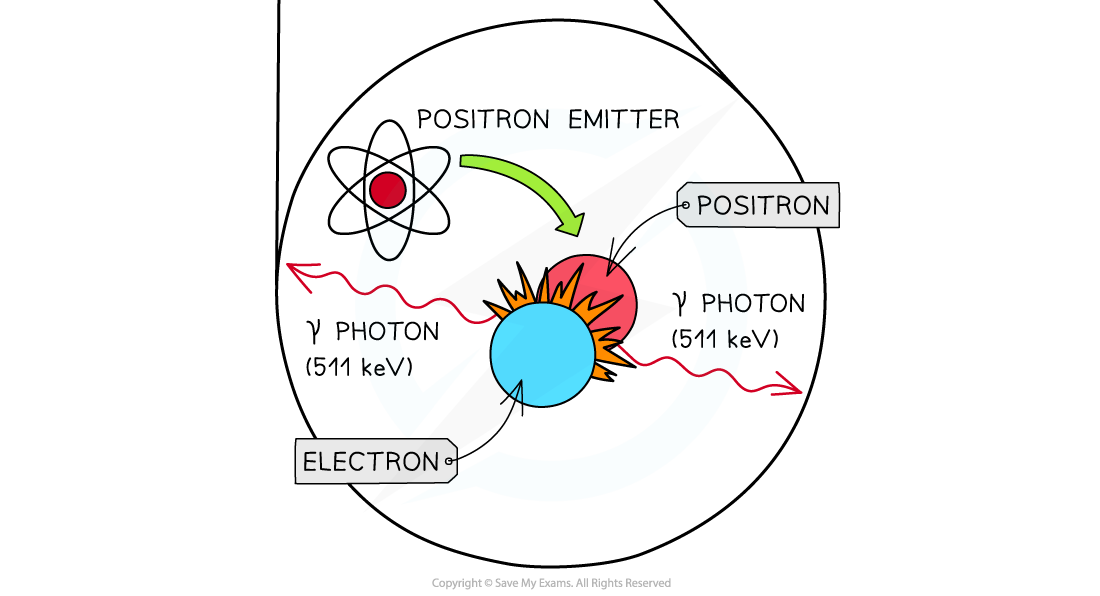
Annihilation

• When a positron is emitted from a tracer in the body, it travels less than a millimetre before it collides with an electron

• The positron and the electron will annihilate, and their mass becomes pure energy in the form of two gamma rays which move apart in opposite directions

• Annihilation doesn’t just happen with electrons and positrons, annihilation is defined as:

  When a particle meets its equivalent antiparticle they are both destroyed and their mass is converted into energy

• As with all collisions, the mass, energy and momentum are conserved

Annihilation of a positron and electron to form two gamma-ray photons

• The gamma-ray photons produced have an energy and frequency that is determined solely by the mass-energy of the positron-electron pair

• The energy E of the photon is given by

E = hf = m_ec²

• The momentum p of the photon is given by

• Where:

  • m_e = mass of the electron or positron (kg)

  • h = Planck's constant (J s)

  • f = frequency of the photon (Hz)

  • c = the speed of light in a vacuum (m s^–1)

Diagnosis Using PET Scanning

• Once the tracer is introduced to the body it has a short half-life, so, it begins emitting positrons (β⁺) immediately

  • This allows for a short exposure time to the radiation

  • A short half-life does mean the patient needs to be scanned quickly and not all hospitals have access to expensive PET scanners

• In PET scanning:

  • Positrons are emitted by the decay of the tracer

  • They travel a small distance and annihilate when they interact with electrons in the tissue

  • This annihilation produces a pair of gamma-ray photons which travel in opposite directions

Annihilation of a positron and an electron is the basis of PET Scanning

Image Formation on a Computer

• The signals produced by the photomultiplier tubes are used to produce an image

• The γ rays travel in straight lines in opposite directions when formed from a positron-electron annihilation

  • This happens in order to conserve momentum

• They hit the detectors in a line – known as the line of response

• The tracers will emit lots of γ rays simultaneously, and the computers will use this information to create an image

• The more photons from a particular point, the more tracer that is present in the tissue being studied, and this will appear as a bright point on the image

• An image of the tracer concentration in the tissue can be created by processing the arrival times of the gamma-ray photons