A LevelPhysicsOCRRevision Notes6. Particles & Medical PhysicsX-raysCalculating X-ray Attenuation

Calculating X-ray Attenuation (OCR A Level Physics): Revision Note

Exam code: H556

Katie M

Author

Katie M

Last updated

Attenuation of X-rays in Matter

  • Bones absorb X-ray radiation

    • This is why they appear white on the X-ray photograph

  • When the collimated beam of X-rays passes through the patient’s body, they are absorbed and scattered

  • The attenuation of X-rays can be calculated using the equation:

I = I0 e−μx

  • Where:

    • I0 = the intensity of the incident beam (W m-2)

    • I = the intensity of the transmitted beam (W m-2)

    • μ = the linear absorption coefficient (m-1)

    • x = distance travelled through the material (m)

  • The attenuation coefficient also depends on the energy of the X-ray photons

  • The intensity of the X-ray decays exponentially

  • The thickness of the material that will reduce the X-ray beam or a particular frequency to half its original value is known as the half thickness

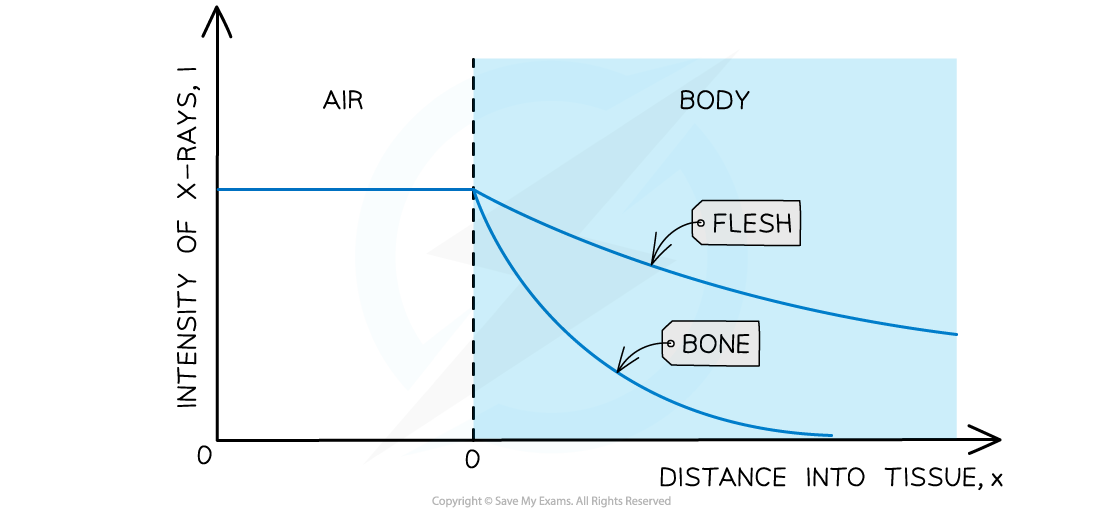
Attenuation of X-rays, downloadable AS & A Level Physics revision notes

Absorption of X-rays by different materials

Worked Example

A student investigates the absorption of X-ray radiation in a model arm. A cross-section of the model arm is shown in the diagram.

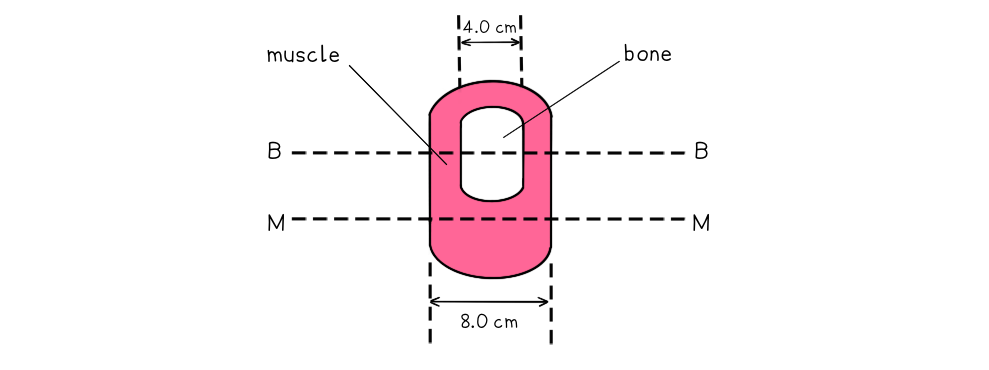
Parallel X-ray beams are directed along the line MM and along the line BB. The linear absorption coefficients of the muscle and the bone are 0.20 cm-1 and 12 cm-1 respectively.

Calculate the ratio:

fraction numerator i n t e n s i t y space o f space e m e r g e n t space X minus r a y space b e a m space f r o m space m o d e l over denominator i n t e n s i t y space o f space e m e r g e n t space X minus r a y space b e a m space o n space m o d e l end fraction

for a parallel X-ray beam directed along the line

a) MM

b) BB

and state whether the X-ray images are sharp, or have good contrast.

Answer:

Part (a)

Step 1: Write out the known quantities

  • Linear absorption coefficient for muscle, μ = 0.20 cm-1

  • Distance travelled through the muscle, x = 8.0 cm

Step 2: Write out the equation for attenuation and rearrange

I = I0 e−μx

fraction numerator i n t e n s i t y space o f space e m e r g e n t space X minus r a y space b e a m space f r o m space m o d e l over denominator i n t e n s i t y space o f space e m e r g e n t space X minus r a y space b e a m space o n space m o d e l end fraction equals I over I subscript 0 equals e to the power of negative mu x end exponent

Step 3: Substitute in values and calculate the ratio

Attenuation of X-rays in Matter Worked Example equation 3

Part (b)

Step 1: Write out the known quantities

  • Linear absorption coefficient for muscle, μm = 0.20 cm-1

  • Linear absorption coefficient for bone, μb = 12 cm-1

  • Distance travelled through the muscle, xm = 4.0 cm

  • Distance travelled through the bone, xb = 4.0 cm

Step 2: Write out the equation for attenuation for two media and rearrange

Attenuation of X-rays in Matter Worked Example equation 4

Step 3: Substitute in values and calculate the ratio

Attenuation of X-rays in Matter Worked Example equation 5

Step 4: Write a concluding statement

  • Each ratio gives a measure of the amount of transmission of the beam

    • A good contrast is when:

      • There is a large difference between the intensities

      • The ratio is much less than 1.0

    • Therefore, both images have a good contrast

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself
    Previous:X-ray Attenuation MechanismsNext:X-ray Imaging
    Katie M

    Author: Katie M

    Expertise: Physics Content Creator

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.