X-Ray Tube (OCR A Level Physics) : Revision Note
Structure of an X-ray Tube
An X-ray tube is a device that converts an electrical input into X-rays
It is composed of four main components:
A heated cathode
An anode
A metal target
A high voltage power supply
The production of X-rays has many practical uses, such as in:
Medical imaging (radiography)
Security
Industrial imaging
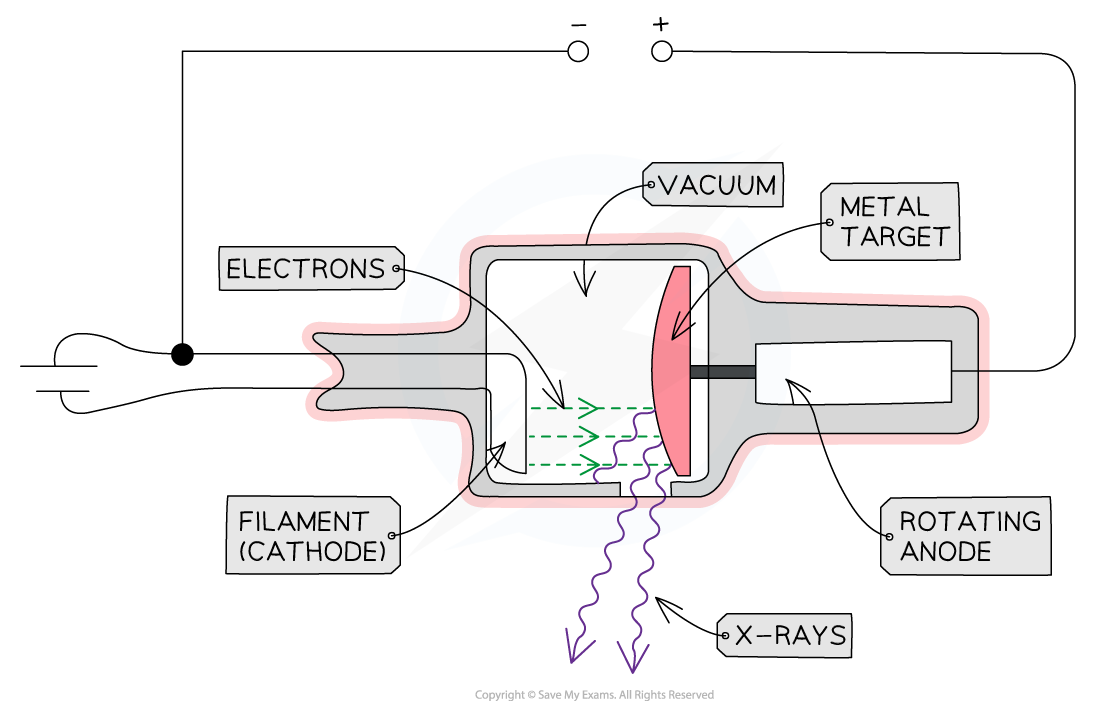
The main components of an X-ray Tube are the heated cathode, anode, metal target and a high voltage supply
The Role of the Components
Heated Cathode
At one end of the tube is the cathode (negative terminal) which is heated by an electric current
The heat causes electrons to be liberated from the cathode, gathering in a cloud near its surface
This process of thermionic emission is the source of the electrons
Anode
At the other end of the tube, an anode (positive terminal) is connected to the high voltage supply
This allows the electrons to be accelerated up to a voltage of 200 kV
When the electron arrives at the anode, its kinetic energy is 200 keV (by the definition of an electronvolt)
Only about 1% of the kinetic energy is converted to X-rays
The rest is converted to heat energy
Therefore, to avoid overheating, the anode is spun at 3000 rpm and sometimes water-cooled
Metal Target
When the electrons hit the target at high speed, they lose some of their kinetic energy
This is emitted as X-ray photons
A heat-resistant block of metal, usually Tungsten, is embedded at the end of the anode, facing the cathode
This is the material that the electrons collide with and X-rays are generated in
High Voltage Power Supply
The high voltage supply creates a large potential difference (> 50 kV) between the cathode and the target
This causes electrons in the cloud around the cathode to be accelerated to a high velocity towards the target, which they strike, creating X-rays
Other Components
X-rays are produced in all directions, so the tube is surrounded by lead shielding
This is to ensure the safety of the operators and recipients of the X-rays
An adjustable window allows a concentrated beam of X-rays to escape and be controlled safely
The anode and cathode are housed inside a vacuum chamber
This is to ensure that the electrons do not collide with any particles on their way to the metal target
Production of X-ray Photons
When the fast-moving electrons collide with the target, X-rays are produced by one of two methods
Method 1: Bremsstrahlung
Method 2: Characteristic Radiation
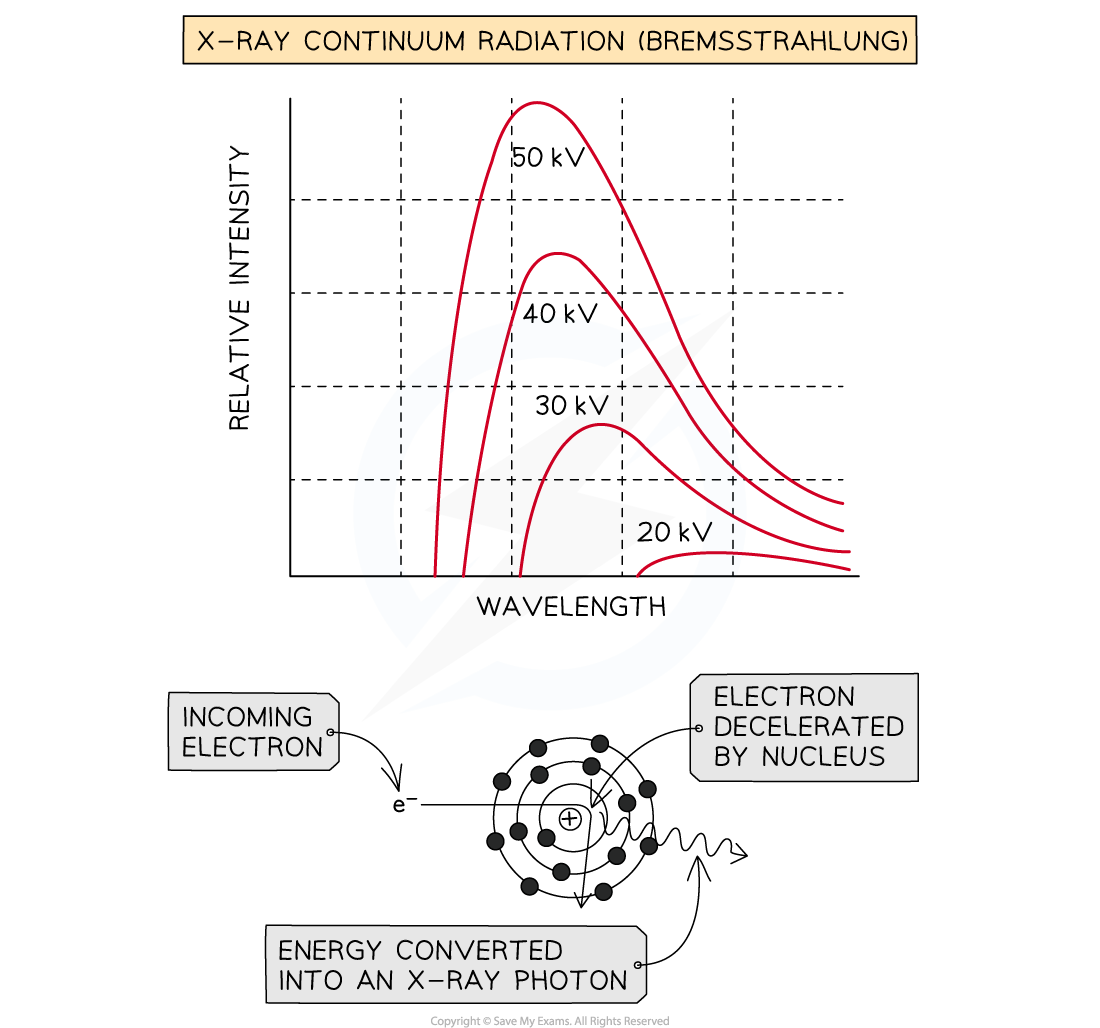
Method 1: Bremsstrahlung
When the high-speed electrons collide with the metal target, they undergo a steep deceleration
When a charged particle decelerates quickly, some of the energy released is converted into a photon
A small amount of the kinetic energy (~ 1%) from the incoming electrons is converted into X-rays as the electrons decelerate in the tungsten, due to conservation of energy
The rest of the energy heats up the anode, which usually requires some form of cooling
The energy of the X-ray photon can be of any value, up to the original kinetic energy of the electron, giving a spread of possible X-ray energies
These X-rays cause the continuous or ‘smooth hump shaped’ line on an intensity wavelength graph
When an electron is accelerated, it gains energy equal to the electronvolt, this energy can be calculated using:
Emax = eV
This is the maximum energy that an X-ray photon can have
The smallest possible wavelength is equivalent to the highest possible frequency and therefore, the highest possible energy
This is assuming all of the electron’s kinetic energy has turned into electromagnetic energy
Therefore, the maximum X-ray frequency fmax, or the minimum wavelength λmin, that can be produced is calculated using the equation:
The maximum X-ray frequency, fmax, is therefore equal to:
The minimum X-ray wavelength, λmin, is therefore equal to:
Where:
e = elementary charge (C)
V = potential difference between the anode and cathode (V)
h = Planck's constant (J s)
c = the speed of light (m s−1)
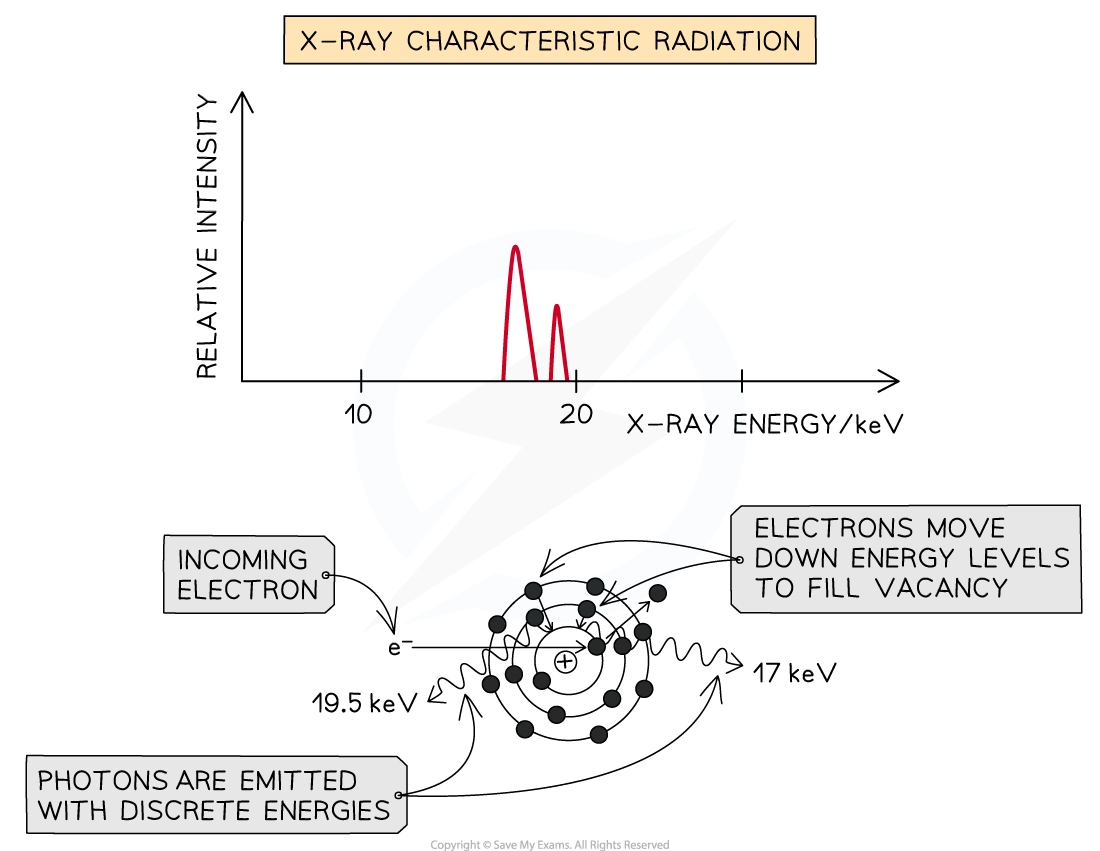
Method 2: Characteristic Radiation
Some of the incoming fast electrons cause inner shell electrons of the tungsten to be ‘knocked out’ of the atom, leaving a vacancy
This vacancy is filled by an outer electron moving down and releasing an X-ray photon as it does (equal in energy to the difference between the two energy levels)
Because these X-rays are caused by energy level transitions, they have only specific discrete energies
They cause sharp spikes on an intensity wavelength graph
The number of spikes depends on the element used for the target - there are two sets of spikes for a tungsten target, representing two sets of possible energy transitions
Worked Example
X-rays are a type of electromagnetic wave with wavelengths in the range 10−8 to 10−13 m
If the accelerating potential difference in an X-ray tube is 60 kV, determine if the photons emitted fall within this range.
Answer:
Step 1: Write out known quantities
Charge on an electron, e = 1.6 × 10−19 C
Accelerating potential difference, V = 60 000 V
Planck’s constant, h = 6.63 × 10−34 J s
Speed of light, c = 3 × 108 m s−1
Step 2: Determine the maximum possible energy of a photon
The maximum possible energy of a photon corresponds to the maximum energy an electron could have:
Emax = eV
Step 3: Determine an expression for minimum wavelength
Planck relation: E = hf
Wave equation: c = fλ
When energy is a maximum:
Emax = eV = hfmax
Maximum energy corresponds to a minimum wavelength:
Rearrange for minimum wavelength, λmin:
Step 4: Calculate the minimum wavelength λmin
λmin = 2.1 × 10−11 m
Step 5: Comment on whether this is within the range for the wavelength of an X-ray
X-ray wavelengths are within 10−8 to 10−13 m
The minimum wavelength for a 60 kV supply is 2.1 × 10−11 m, which means the photons produced will be X-rays
Worked Example
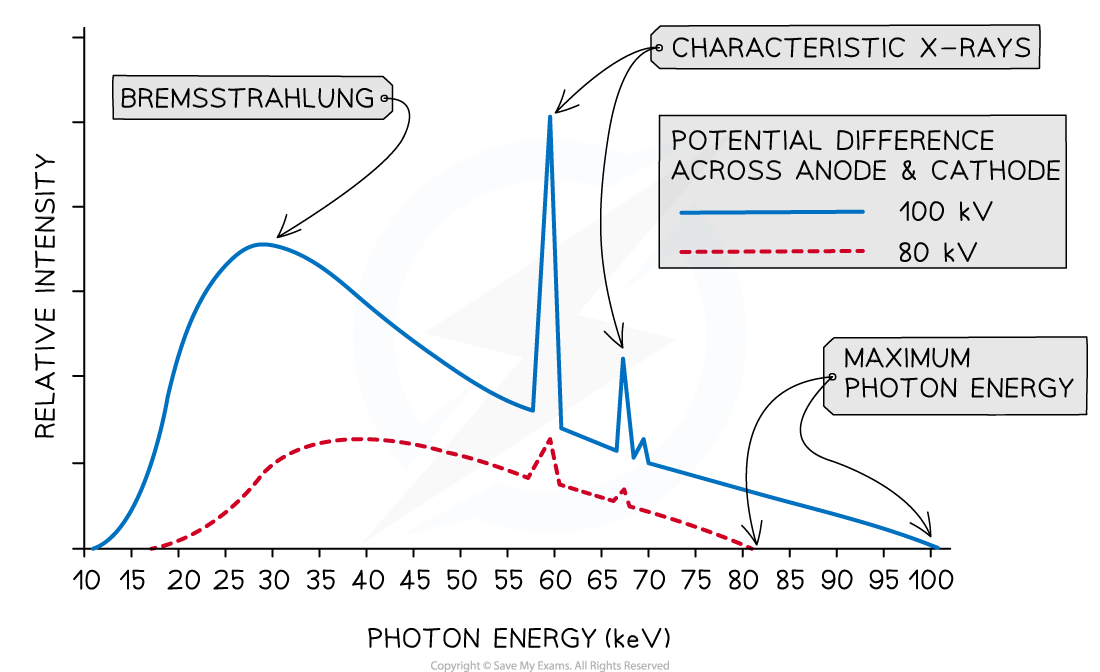
A typical spectrum of the X-ray radiation produced by electron bombardment of a metal target is shown below.
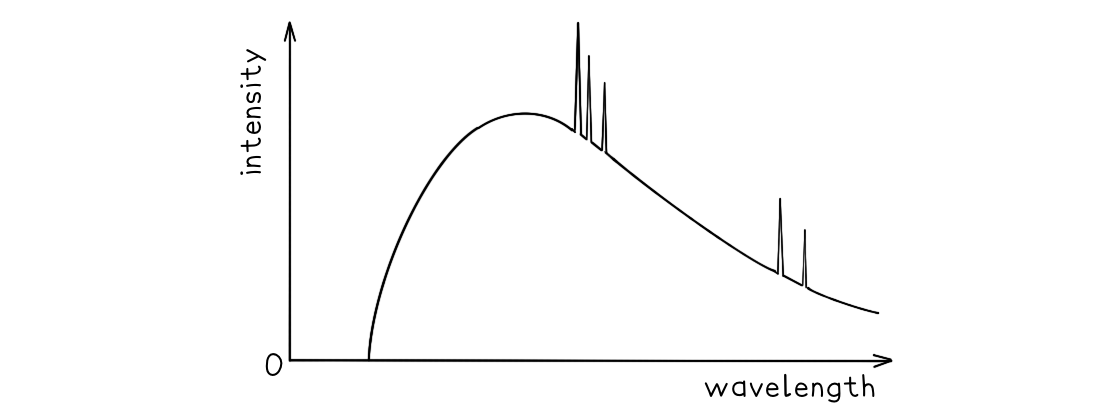
Explain why:
a) A continuous spectrum of wavelengths is produced.
b) The gradient is steeper at shorter wavelengths.
c) The spectrum has a sharp cut-off at short wavelengths.
Answer:
Part (a)
Step 1: Consider the path of the electrons from the cathode to the anode
Photons are produced whenever a charged particle undergoes a large acceleration or deceleration
X-ray tubes fire high-speed electrons at a metal target
When an electron collides with the metal target, it loses energy in the form of an X-ray photon as it decelerates
Step 2: Consider the relationship between the energy of the electron and the wavelength of the photon
The wavelength of a photon depends on the energy transferred by a decelerating electron
The electrons don't all undergo the same deceleration when they strike the target
This leads to a distribution of energies, hence, a range, or continuous spectrum, of wavelengths is observed
Part (b)
Step 1: Identify the significance of the intensity
The intensity of the graph signifies the proportion of photons produced with a specific energy, or wavelength
The higher the intensity, the more photons of a particular wavelength are produced
In other words, the total intensity is the sum of all the photons with a particular wavelength
Step 2: Explain the shape of the graph
When a single electron collides with the metal target, a single photon is produced
Most electrons only give up part of their energy, and hence there are more X-rays produced at wavelengths higher than the minimum (or energies lower than the maximum)
At short wavelengths, there is a steeper gradient because only a few electrons transfer all, or most of, their energy
Part (c)
Step 1: Identify the relationship between minimum wavelength and maximum energy
The minimum wavelength of an X-ray is equal to
The equation shows the maximum energy of the electron corresponds to the minimum wavelength, they are inversely proportional
Therefore, the higher the energy of the electron, the shorter the wavelength of the X-ray produced
Step 2: Explain the presence of the cut-off point
The accelerating voltage determines the kinetic energy which the electrons have before striking the target
The value of this accelerating voltage, therefore, determines the value of the maximum energy
This corresponds to the minimum, or cut-off, wavelength

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
