A LevelPhysicsOCRRevision Notes5. Newtonian World & Astrophysics5.9 Gravitational Potential & Energy5.9.3 Force-Distance Graph

Force-Distance Graph (OCR A Level Physics)

Revision Note

Test yourself
Katie M

Author

Katie M

Last updated

Force Distance Graphs for Point or Spherical Masses

  • Recall that Newton's Law of Gravitation says the magnitude of the force F between a mass M and a mass m is given by the equation:

F equals fraction numerator G M m over denominator r squared end fraction

  • Therefore, a force-distance graph would be a curve, because F is inversely proportional to r2, or:

F proportional to 1 over r squared

 

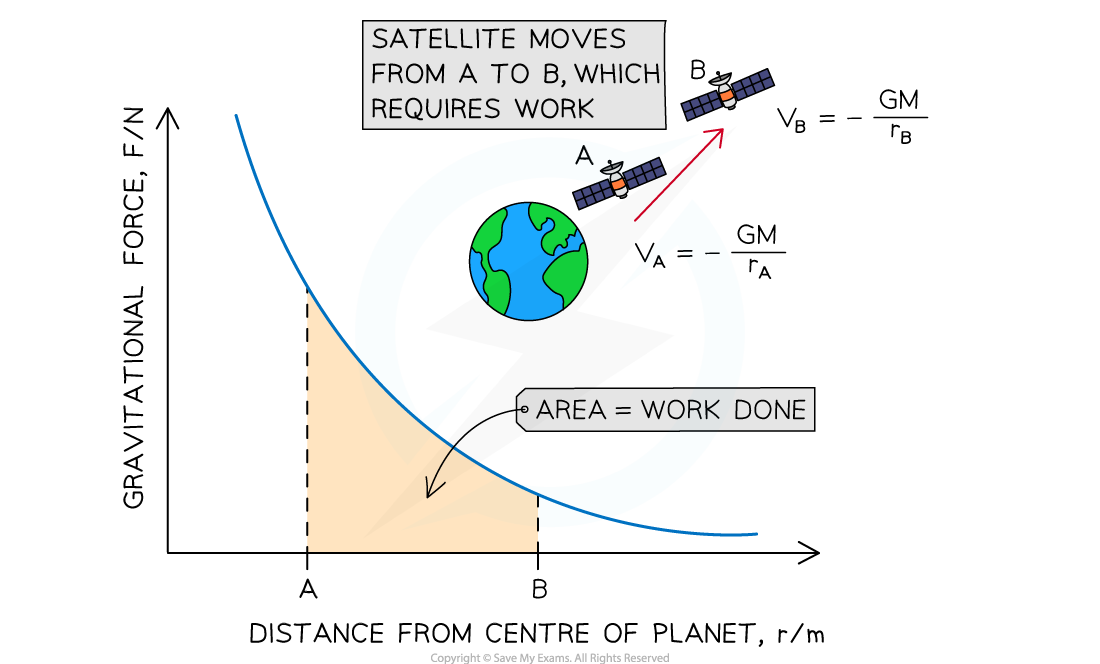
5-9-3-force-distance-graph_ocr-al-physics

Work is done on the satellite of mass m to move it from A to B, because gravity is attractive. The area under the curve represents the magnitude of energy transferred

  • The product of force and distance is equal to work done (or energy transferred) 
  • Therefore, the area under the force-distance graph for gravitational fields is equal to the work done
    • In the case of a mass m moving further away from a mass M, the potential increases
    • Since gravity is attractive, this requires work to be done on the mass m
    • The area between two points under the force-distance curve therefore gives the change in gravitational potential energy of mass m

Examiner Tip

You should be able to interpret areas under curves by thinking about what the product of the quantities on the axes would represent. Since, in this case, force × distance = work done, then it follows that the area under the curve represents the change in energy between two points. Specifically, this would be a change in gravitational potential energy!

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:5.9.2 Calculating Gravitational PotentialNext:5.9.4 Gravitational Potential Energy
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.