Gravitational Potential (OCR A Level Physics)

Gravitational Potential

Near the Earth's Surface

• The gravitational potential energy (G.P.E) is the energy an object has when lifted off the ground given by the familiar equation:

G.P.E = mgΔh

• When using this equation, the G.P.E on the surface of the Earth is taken to be zero

  • This means work is done to lift the object

• This equation can only be used for objects that are near the Earth's surface

  • This is because, near Earth's surface, the gravitational field is approximated to be uniform

  • Far away from the Earth's surface, the gravitational field is radial because the Earth is a sphere

In a Radial Field

• In a radial field, G.P.E is defined as the energy an object possesses due to its position in a gravitational field

• The gravitational potential at a point is the gravitational potential energy per unit of mass for an object at that point

• Gravity is always attractive, so work must be done on a mass to move it away to a point infinitely far away from every other mass

  • 'Infinity' is the point at which the gravitational potential is zero

  • Therefore, since the potential energy of all masses increases as work is done on them to move them infinitely far away, the value of the potential is always negative

• Gravitational potential is formally defined as:

  The work done per unit of mass in bringing a mass from infinity to a defined point

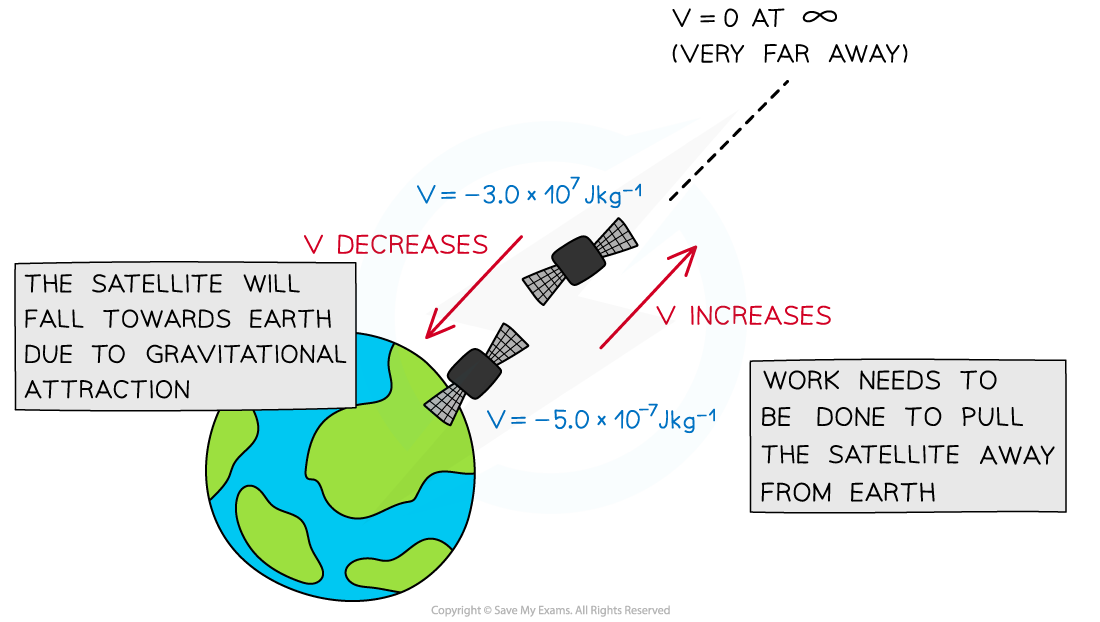
Gravitational potential decreases as the satellite moves closer to the Earth. It increases if it moves further away, towards infinity, where gravitational potential is zero