Newton's Law of Gravitation

The gravitational force between two masses, e.g., between the Earth and the Sun, is defined by Newton’s Law of Gravitation
Newton’s Law of Gravitation states:

The gravitational force F between two masses m₁ and m₂ is proportional to the product of their masses and inversely proportional to the square of their separation, r

In equation form, this is written as:

$F = - \frac{G m_{1} m_{2}}{r^{2}}$

Where:
- F = gravitational force between two point masses m₁ and m₂ (N)
- G = Newton’s gravitational constant
- m₁ and m₂ = mass of body 1 and mass of body 2 (kg)
- r = distance between the centre of the two masses (m)
The 1/r² relation is called the ‘inverse square law’
- This means that if the distance between two masses doubles, r becomes 2r
- Therefore, 1/r² becomes 1/(2r)², which is equal to 1/4r²
- Hence, the gravitational force between the two masses reduces by a factor of four

The negative sign indicates that the gravitational force F between the two point masses m₁ and m₂ is attractive

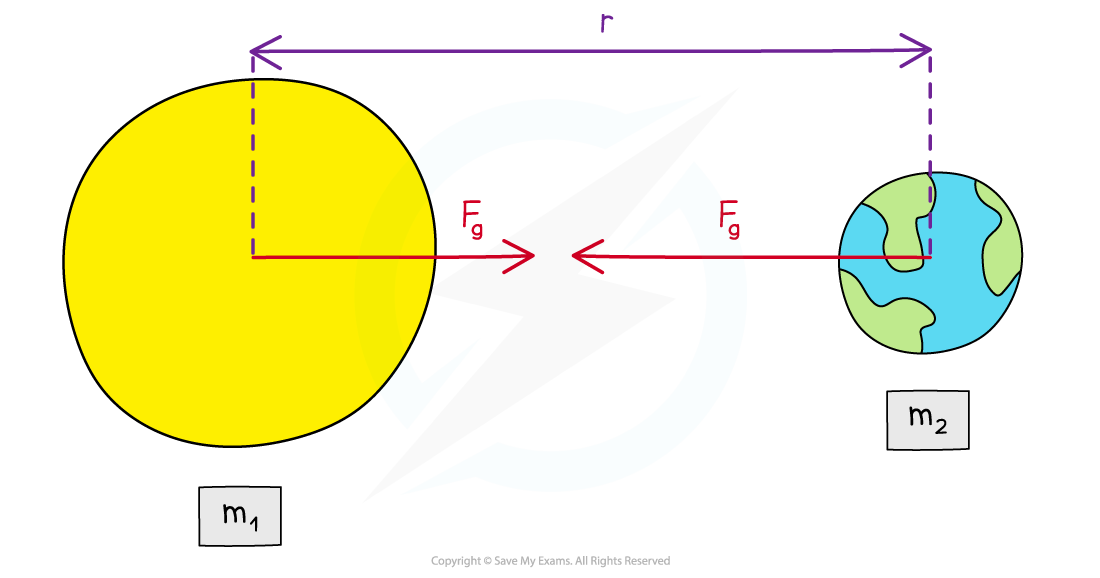
Newton's law of gravitation, downloadable AS & A Level Physics revision notes

The gravitational force between two masses is defined by Newton’s Law of Gravitation

Worked example

A satellite with mass 6500 kg is orbiting the Earth at 2000 km above the Earth's surface. The magnitude of the gravitational force between them is 37 kN.

Calculate the mass of the Earth.

(Radius of the Earth = 6400 km)

Examiner Tip

A few common mistakes to be aware of are:

forgetting to add together the distance from the surface of the planet and its radius to obtain the value of r. The distance r is measured between the centre of each mass, which is from the centre of the planet to the centre of the satellite!
forgetting that the distance between point masses m₁ and m₂ is squared. Remember this whenever you use Newton's Law of Gravitation!
Note in this worked example, we calculated the magnitude of the gravitational force F. Therefore, we could ignore the negative sign. Make sure you are aware of this!

Newton's Law of Gravitation (OCR A Level Physics)

Revision Note