Gravitational Field Strength (OCR A Level Physics): Revision Note
Exam code: H556
Gravitational Field Strength
There is a universal force of attraction between all matter with mass
This force is known as the ‘force due to gravity’ or the weight
The Earth’s gravitational field is responsible for the weight of all objects on Earth
The gravitational field strength g at a point is defined as force F per unit mass m of an object at that point:
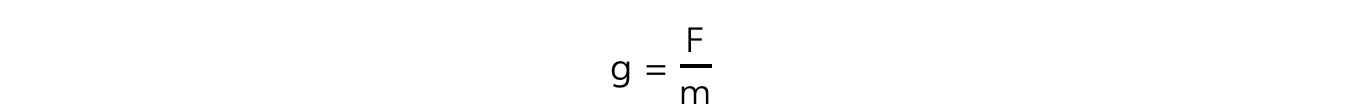
Where:
g = gravitational field strength (N kg–1)
F = force due to gravity, or weight (N)
m = mass (kg)
This equation shows that:
The larger the mass of an object, the greater its pull on another mass
On planets with a large value of g, the gravitational force per unit mass is greater than on planets with a smaller value of g
An object's mass remains the same at all points in space
However, on planets such as Jupiter, the weight of an object will be a lot greater than on a less massive planet, such as Earth
This means the gravitational force would be so high that humans, for example, would not be able to fully stand up (or, even worse...)

The weight force on Jupiter would be so large that even standing upright would be difficult
Factors that affect the gravitational field strength at the surface of a planet are:
The radius (or diameter) of the planet
The mass (or density) of the planet
Worked Example
Calculate the mass of an object with weight 10 N on Earth.
Answer:

Gravitational Field Strength in a Radial Field
In a radial field (due to a point mass M), the gravitational field lines get further apart from each other
This indicates that the strength of the gravitational field decreases with distance from the centre of mass of M
The gravitational field strength g in a radial field, due to some mass M, is given by the equation:
Where:
g = gravitational field strength (N kg–1)
G = Newton's Gravitational constant (N m2 kg–2)
M = mass of the object causing the gravitational field (kg)
r = radial distance from the centre of mass of M (m)
Note:
The negative sign in this equation indicates that the gravitational field is attractive
In other words, the direction of the gravitational field lines is towards the mass M
On the Earth’s surface, g has a constant value of 9.81 N kg-1
However far outside the Earth’s surface, g is not constant
g decreases as r increases by a factor of 1/r2
This is an inverse square law relationship with distance
When the magnitude of g is plotted against the distance from the centre of a planet, r has two parts:
When r < R (the radius of the planet), g is directly proportional to r
When r > R, g is inversely proportional to r2
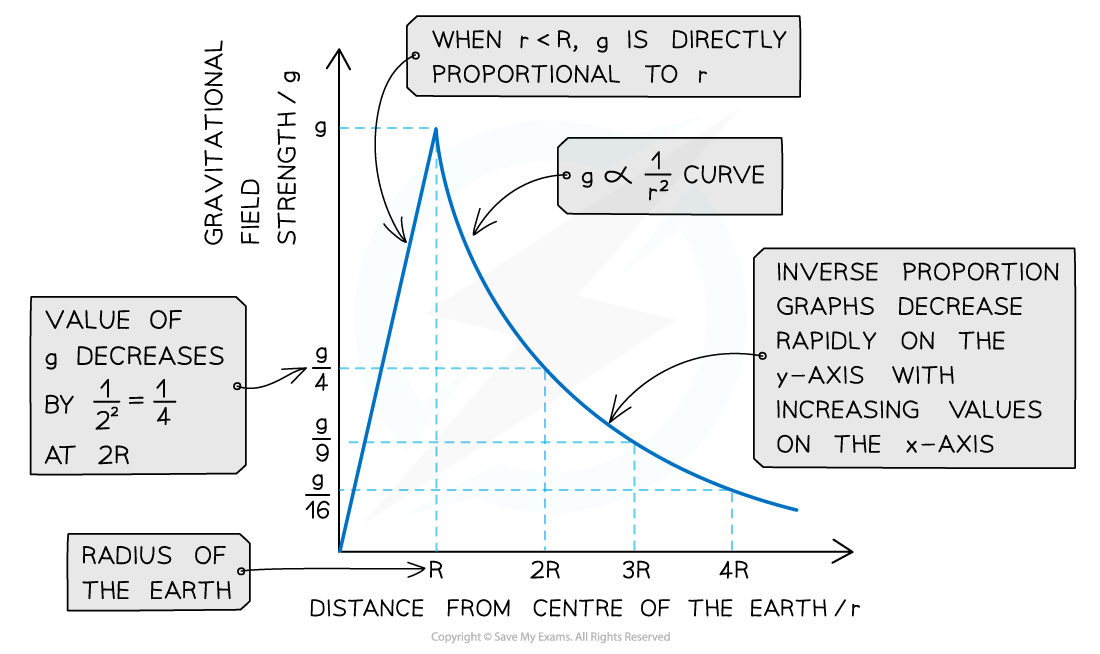
The magnitude of gravitational field strength g against distance r from the Earth's surface follows a 1/r2 relationship
Gravitational Field Strength Close to the Earth's Surface
Near the Earth's surface, the gravitational field is uniform
Hence, the gravitational field lines are parallel and evenly spaced
This means the gravitational field strength is constant at every point near the Earth's surface
Numerically, the gravitational field strength near Earth's surface is equal to the acceleration due to gravity, g = 9.81 m s–2
Worked Example
Determine the distance from the Earth's surface at which the gravitational field strength decreases by a factor of 0.5.
(The radius of the Earth is 6400 km and its mass is 6.0 × 1024 kg)
Answer:
Step 1: Write the known quantities
Radius of the Earth RE = 6400 km = 6400 × 103 m
Mass of the earth ME = 6.0 × 1024 kg
Gravitational constant G = 6.67 × 10–11 N m2 kg–2
Step 2: Recall the value of the gravitational field strength at the Earth's surface
The gravitational field strength at the Earth's surface g = 9.81 N kg–1
Step 3: Write the equation for gravitational field strength in a radial field
The Earth creates a radial gravitational field (far from its surface) therefore the equation for gravitational field strength g is:
Step 4: Determine the distance r at which the field strength reduces by a factor of 0.5
If the field strength decreases by a factor of 0.5, then g × 0.5 = 9.81 × 0.5 = 4.905 N kg–1
Therefore, ignoring the negative sign (as we only want a magnitude):
4.905 =
r2 =
r = = 9.0 × 106 m
Step 5: Determine the distance from the Earth's surface
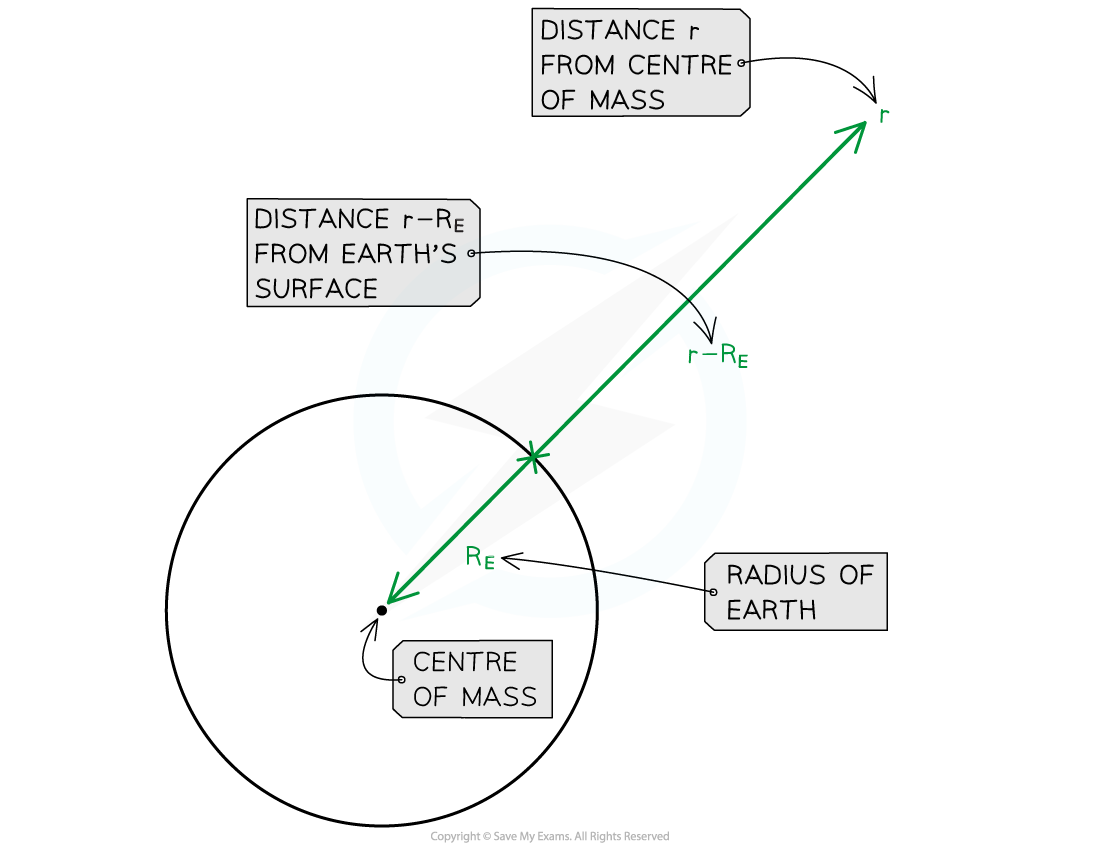
The value r = 9.0 × 106 m is the radial distance from the Earth's centre of mass
Therefore, the gravitational field strength reduces by a factor 0.5 at a distance r – RE
r – RE = (9.0 × 106) – (6400 × 103) = 2.6 × 106 m
Examiner Tips and Tricks
The equation for the gravitational field strength in a radial field is in terms of the distance r from the centre of mass of mass M. If the exam question is about a planet, remember that you might have to take the planet's radius into account, which is the distance between its centre of mass and its surface! As ever, drawing a labelled diagram of the distances in question really helps.

Unlock more, it's free!
Did this page help you?