Velocity (OCR A Level Physics)

• The velocity of an object in simple harmonic motion varies as it oscillates back and forth
  • Since velocity is a vector, the velocity of the oscillator is its speed in a certain direction

• The maximum velocity of an oscillator is at the equilibrium position i.e. when its displacement is 0 (x = 0)
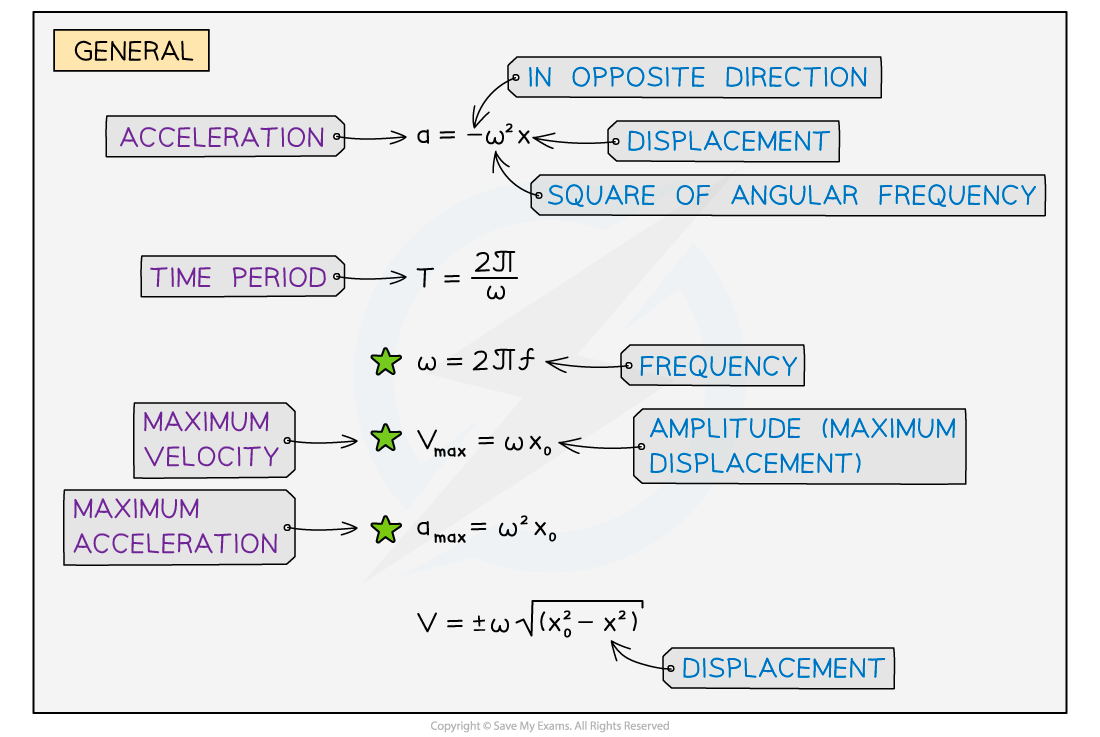
• The velocity of an oscillator in SHM is defined by:

v = v₀ cos(⍵t)

• Where:
  • v = velocity (m s^-1)
  • v₀ = maximum velocity (m s^-1)
  • ⍵ = angular frequency (rad s^-1)
  • t = time (s)

• This is a cosine function if the object starts oscillating from the equilibrium position (x = 0 when t = 0)
• How the velocity v changes with the oscillator’s displacement x is defined by:

• Where:
  • x = displacement (m)
  • x₀ = amplitude (m)
  • ± = ‘plus or minus’. The value can be negative or positive

• This equation shows that when an oscillator has a greater amplitude x₀, it has to travel a greater distance in the same time and hence has greater velocity, v
• When the velocity is at its maximum (at x = 0), the equation becomes:

v₀ = ⍵x₀

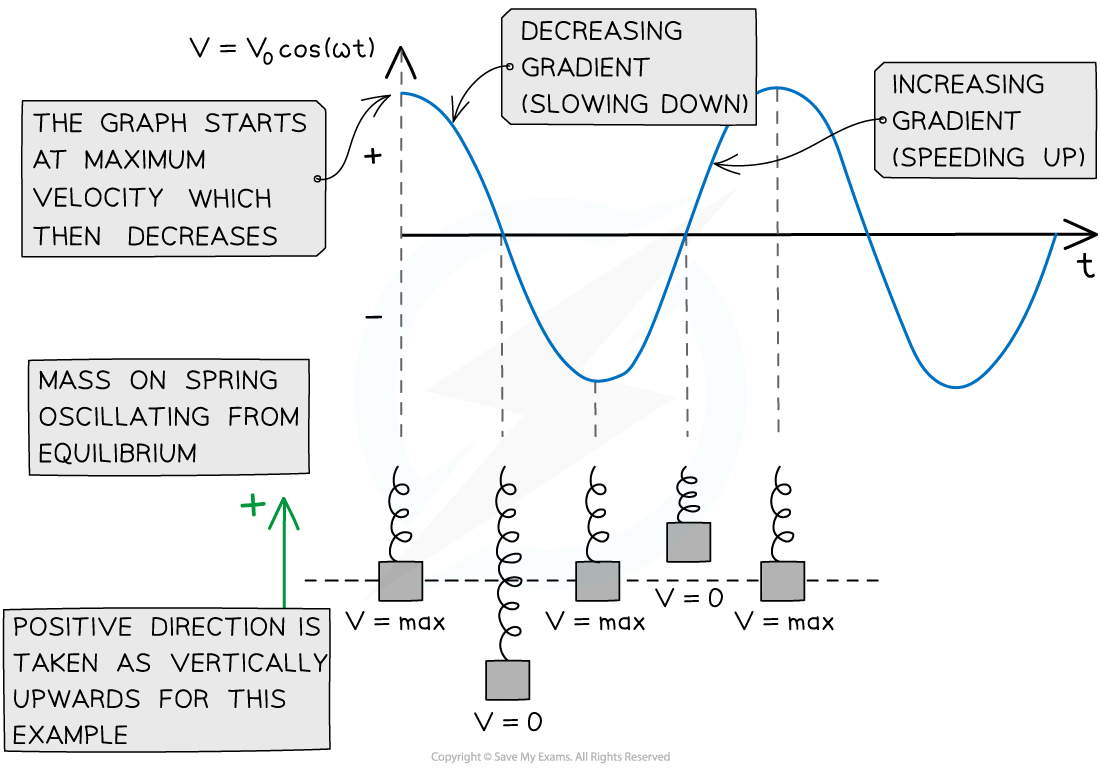
The variation of the speed of a mass on a spring in SHM over one complete cycle

Step 1: Write out the known quantities

• • Amplitude of oscillations, x₀ = 15 cm = 0.15 m
  • Displacement at which the speed is to be found, x = 12 cm = 0.12 m
  • Frequency, f = 6.7 Hz

Step 2: Oscillator speed with displacement equation

• • Since the speed is being calculated, the ± sign can be removed as direction does not matter in this case

Step 3: Write an expression for the angular frequency

• • Equation relating angular frequency and normal frequency:

⍵ = 2πf = 2π× 6.7 = 42.097…

Step 4: Substitute in values and calculate

v = 3.789 = 3.8 m s^-1 (2 s.f)