Revision NotesExam QuestionsPast Papers
A LevelPhysicsOCRRevision Notes5. Newtonian World & AstrophysicsSimple Harmonic OscillationsConditions for Simple Harmonic Motion

Conditions for Simple Harmonic Motion (OCR A Level Physics): Revision Note

Exam code: H556

Katie M

Author

Katie M

Last updated

Simple Harmonic Motion

  • Simple harmonic motion (SHM) is a specific type of oscillation

  • An oscillation is said to be SHM when:

The acceleration of a body is proportional to its displacement, but acts in the opposite direction

  • Acceleration a and displacement x can be represented by the defining equation of SHM:

a space proportional to space minus x

  • The two conditions required for an object to be in simple harmonic motion are therefore:

    • The acceleration is proportional to the displacement

    • The acceleration is in the opposite direction to the displacement

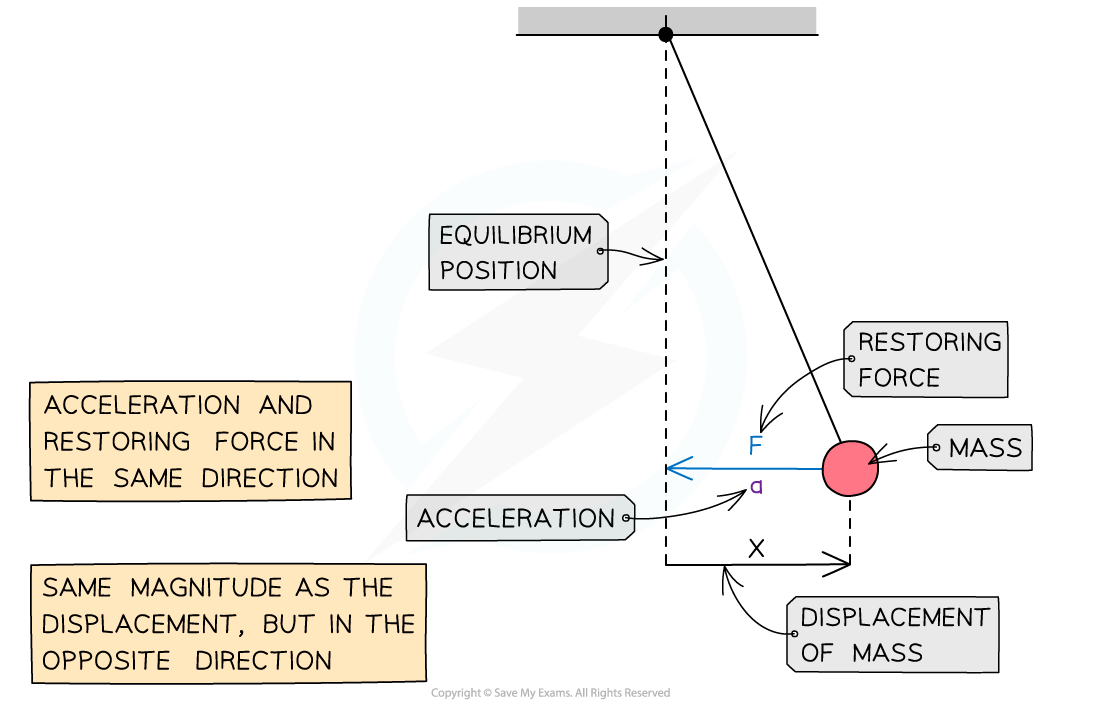
SHM pendulum, downloadable AS & A Level Physics revision notes

Force, acceleration and displacement of a pendulum in SHM

Worked Example

Explain why a person jumping on a trampoline is not an example of simple harmonic motion.

Answer:

Step 1: Recall the conditions for simple harmonic motion

  • The conditions required for SHM:

    • The restoring force/acceleration is proportional to the displacement

    • The restoring force/acceleration is in the opposite direction to the displacement

Step 2: Consider the forces in the scenario given

  • When the person is not in contact with the trampoline, the restoring force is equal to their weight, which is constant

  • The value of their weight does not change, even if they jump higher (increase displacement)

Step 3: Write a concluding sentence

  • The restoring force on the person is not proportional to their distance from the equilibrium position, therefore, this scenario does not fulfil the conditions for SHM

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself
    Previous:Angular FrequencyNext:Time Period & Frequency
    Katie M

    Author: Katie M

    Expertise: Physics Content Creator

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.