Describing Oscillations (OCR A Level Physics): Revision Note
Exam code: H556
Describing Oscillations
An oscillation is defined as follows:
The repetitive variation with time t of the displacement x of an object about the equilibrium position (x = 0)

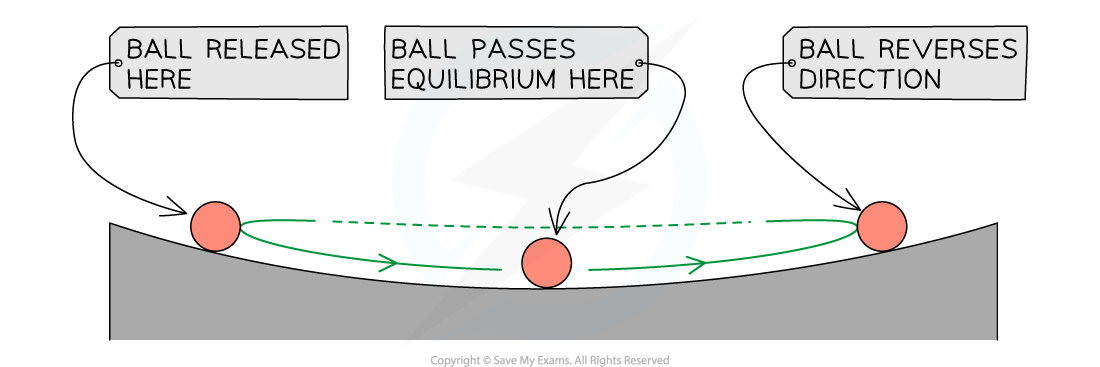
A pendulum oscillates between A and B. On a displacement-time graph, the oscillating motion of the pendulum is represented by a wave, with an amplitude equal to x0
Displacement (x) of a wave is the distance of a point on the wave from its equilibrium position
It is a vector quantity; it can be positive or negative
Period (T) or time period, is the time interval for one complete oscillation, and it is measured in seconds (s)
If the oscillations have a constant period, they are said to be isochronous

The time period of a wave oscillation

A diagram showing one oscillation for both types of SHM
Amplitude (x0) is the maximum value of the displacement on either side of the equilibrium position is known as the amplitude of the oscillation

The diagram shows the amplitude of an oscillation is measured from the central mean position to an extreme position.
Frequency (f) is the number of oscillations per second, and it is measured in hertz (Hz)
The frequency and the period of the oscillations are related by the following equation:

The phase difference between two waves is a measure of how much a point or a wave is in front or behind another
This can be found from the relative positive of the crests or troughs of two different waves of the same frequency
When the crests or troughs are aligned, the waves are in phase
When the crest of one wave aligns with the trough of another, they are in antiphase
The diagram below shows the green wave leads the purple wave by ¼ λ
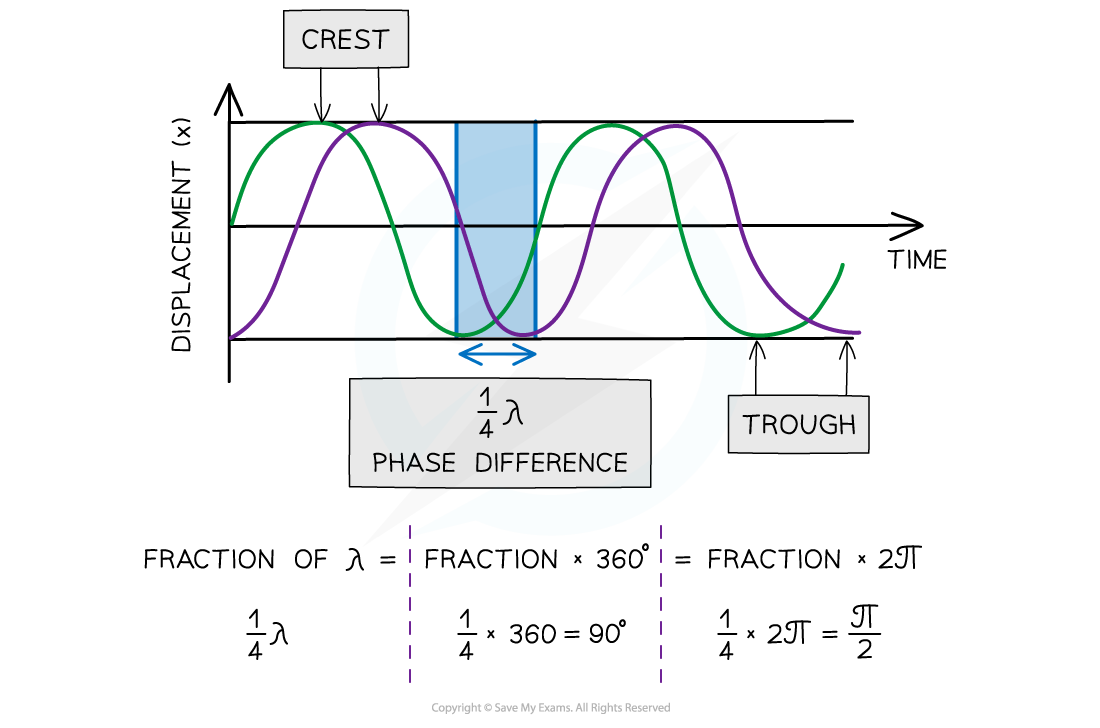
Two waves ¼ λ out of phase
In contrast, the purple wave is said to lag behind the green wave by ¼ λ
Phase difference is measured in fractions of a wavelength, degrees or radians
The phase difference can be calculated from two different points on the same wave or the same point on two different waves
The phase difference between two points can be described as:
In phase is 360o or 2π radians
In anti-phase is 180o or π radians
Worked Example
A child on a swing performs 0.2 oscillations per second. Calculate the period of the child's oscillations.
Answer:
Step 1: Write down the frequency of the swing's oscillations
f = 0.2 Hz
Step 2: Write down the relationship between the period T and the frequency f
Step 3: Substitute the value of the frequency into the above equation and calculate the period
Worked Example
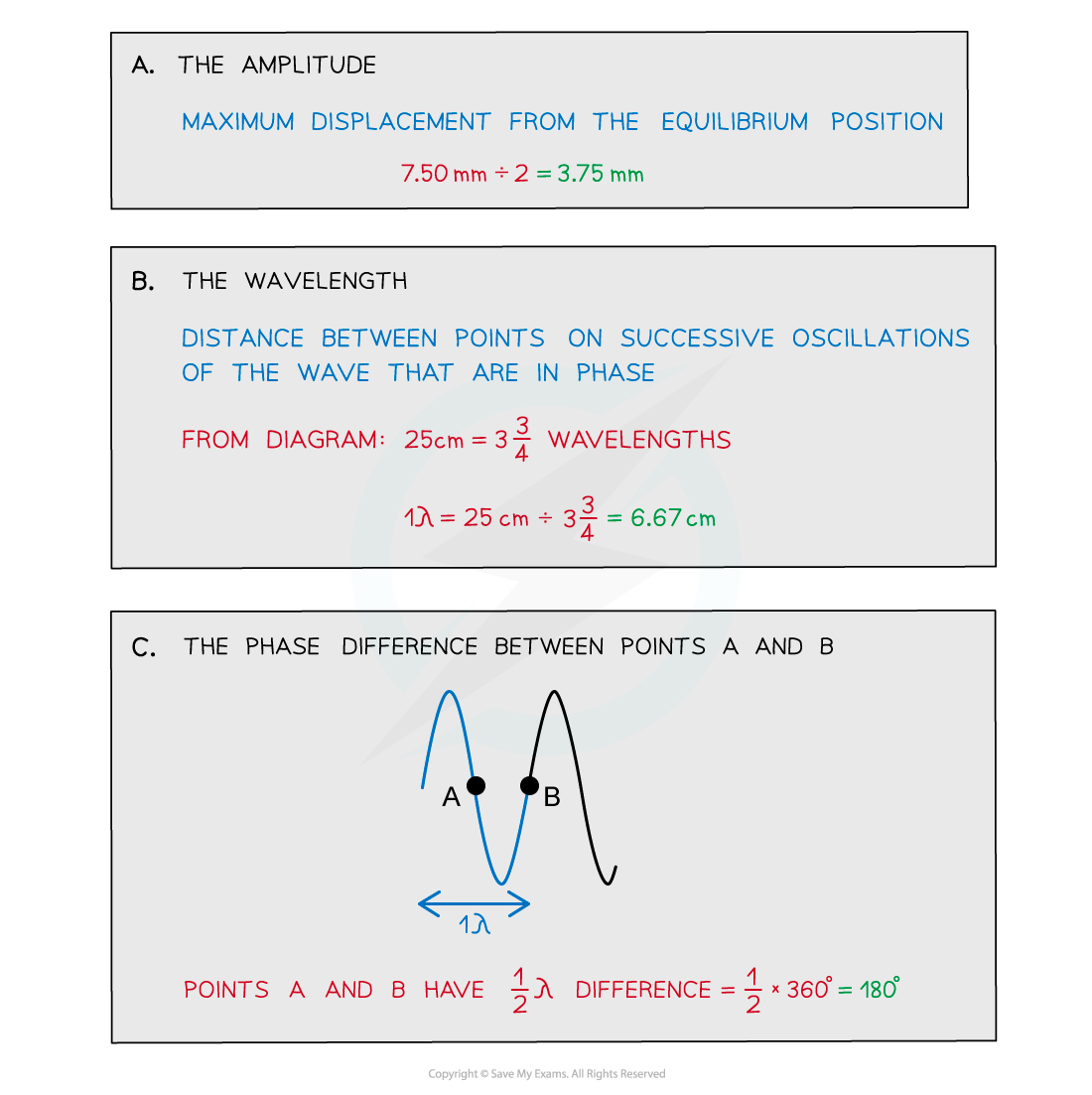
Plane waves on the surface of water at a particular instant are represented by the diagram below.

The waves have a frequency of 2.5 Hz. Determine:
a) The amplitude
b) The wavelength
c) The phase difference between points A and B
Answer:
Examiner Tips and Tricks
When labelling the wavelength and time period on a diagram:
Make sure that your arrows go from the very top of a wave to the very top of the next one
If your arrow is too short, you will lose marks
The same goes for labelling amplitude, don’t draw an arrow from the bottom to the top of the wave, this will lose you marks too.

Unlock more, it's free!
Did this page help you?