Investigating Circular Motion (OCR A Level Physics)

Investigating Circular Motion

Equipment & Method

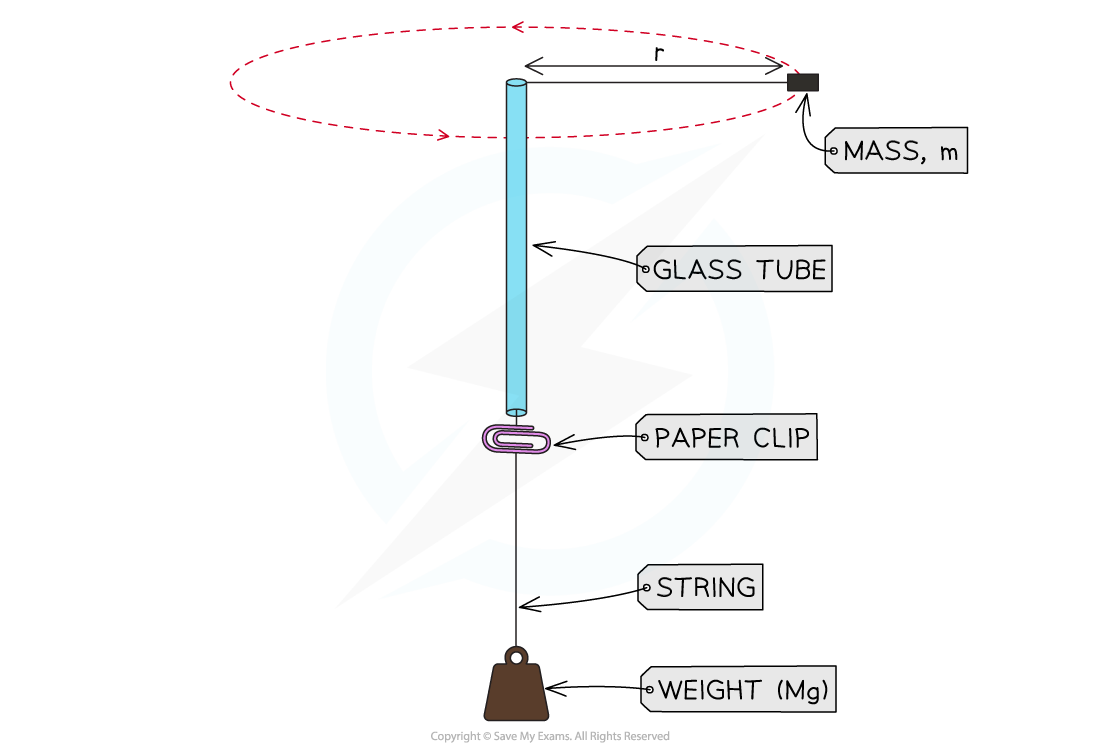
• Circular motion can be investigated using the following setup:

  • Tie a bung of mass m, to a piece of string, which sits horizontally

  • Thread it though a glass tube and a paper clip, which sits vertically

  • At the other end of the string a heavier mass, M is suspended vertically

  • This provides the centripetal force, F = Mg when the tension in the string is constant

• The string is spun in a circle:

  • The time taken for several rotations is recorded and repeated to remove any random errors

• The masses in the experimental set up are changed before the experiment is repeated again

Explanation

• As the bung is swung in a circle the bigger suspended mass, M will remain stationary

  • When the force it provides is equal to the centripetal force, Mg 

  • This is the centripetal force required to make the bung travel in a circular path

• The weight, and hence the centripetal force, required for different masses, radii and speeds can be investigated

• The forces acting on the bung are:

  • The tension in the string

  • The weight of the bung downwards

• If the centripetal force required is greater than its weight then the suspended mass moves upwards

• If the centripetal force required is less than its weight then the suspended mass moves downwards

  • The paperclip will move accordingly to make this movement clearer

• As the bung moves around the circle, the direction of the tension will change continuously

• The magnitude of the tension will also vary continuously, reaching a maximum value at the bottom and a minimum value at the top

  • This is because the direction of the weight of the bung never changes, so the resultant force will vary depending on the position of the bung in the circle

• At the bottom of the circle, the tension must overcome the weight, this can be written as:

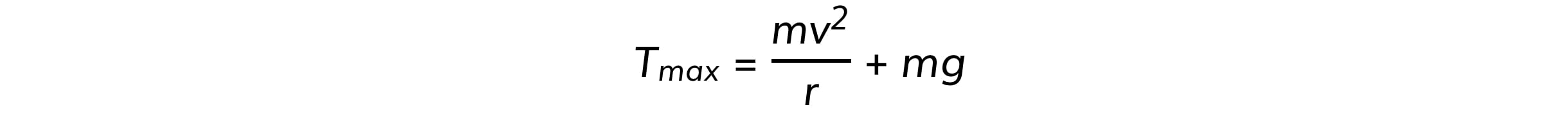
• As a result, the acceleration, and hence, the speed of the bung will be slower at the top

• At the top of the circle, the tension and weight act in the same direction, this can be written as:

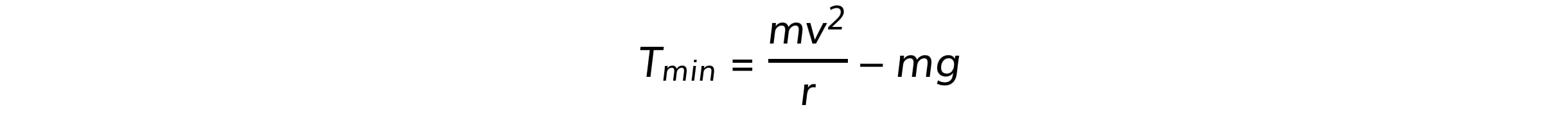
• As a result, the acceleration, and hence, the speed of the bung will be faster at the bottom