Linear Speed (OCR A Level Physics): Revision Note

Constant Speed in a Circle

• An object moving in a straight line at constant speed has an acceleration of zero

  • When that object has a net force applied at right angles to its constant linear speed then it begins to move in a uniform circular motion

•  Whilst the linear speed remains constant the direction of motion is constantly changing

  • So, there is acceleration towards the centre of the circle and the direction of the net force 

When an object is in uniform circular motion, velocity constantly changes direction, but the speed stays the same

• Linear velocity is defined as: 

  The velocity of an object rotating in uniform circular motion, with respect to a linear displacement, as opposed to angular displacement

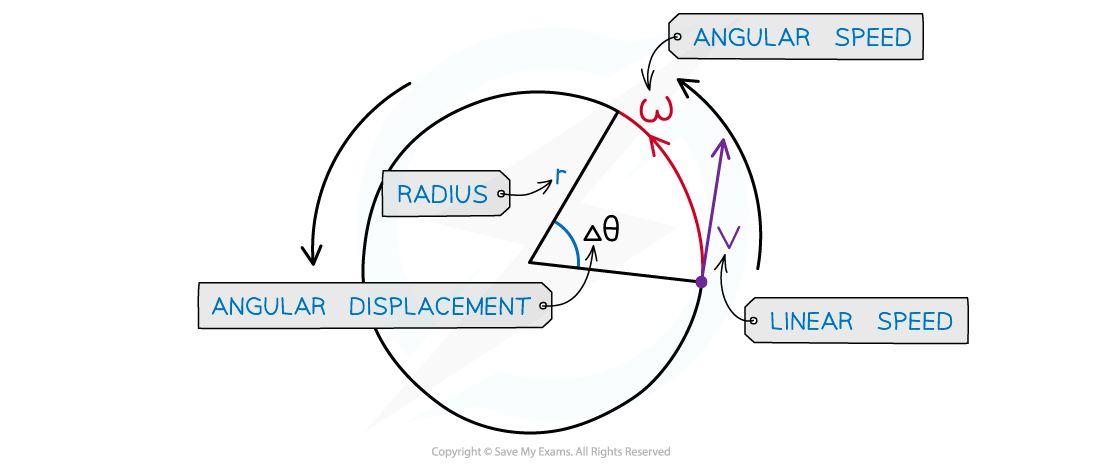
• The linear speed, v, is related to the angular speed, ⍵, by the equation:

v = rω

• Where:

  • v = linear speed (m s^–1)

  • r = radius of circle (m)

  • ⍵ = angular speed (rad s^–1)

• The equation for linear speed can be derived from the definitions for angular displacement and angular velocity

• Linear velocity can be described using the equation:

v  = $\frac{\mathrm{distance}\mathrm{travelled}}{\mathrm{time}\mathrm{taken}}$

• If the distance travelled in a time, t, is equal to the length of an arc of a circle, rθ:

v = $\frac{r\theta }{t}$

• Where:

  • θ = angular displacement (°)

• Since angular velocity is given by:

$\omega =\frac{\theta }{t}$

• The equation for linear speed of an object in circular motion can be written as

$v=r\left(\frac{\theta }{t}\right)=r\omega$

v = rω

• This equation shows:

  • As the radius, r, of the path increases so does the linear velocity, v

• Therefore, it can be seen: 

  • The angular speed and velocity do not depend on the radius of the circle

  • The linear speed, however, does depend on the radius of the circle