Centripetal Force (OCR A Level Physics): Revision Note
Exam code: H556
Net Force on an Object in a Circular Path
For an object moving in a circle, it will have the following properties:
Period
Frequency
Angular displacement
Angular velocity
These properties can be inferred from the properties of objects moving in a straight line combined with the geometry of a circle
Motion in a Straight Line
When an object moves in a straight line at a constant speed its motion can be described as follows:
The object moves at a constant velocity, v
Constant velocity means zero acceleration, a
Newton's First Law of motion says the object will continue to travel in a straight line at a constant speed unless acted on by another force
Newton's Second Law of motion says for zero acceleration that there is no net or resultant force
For example, an ice hockey puck moving across a flat frictionless ice rink
Motion in a Circle
If one end of a string was attached to the puck, and the other attached to a fixed point, it would no longer travel in a straight line, it would begin to travel in a circle
The motion of the puck can now be described as follows:
As the puck moves it stretches the string a little to a length r
The stretched string applies a force to the puck pulling it so that it moves in a circle of radius r around the fixed point
The force acts at 90° to the velocity so there is no force component in the direction of velocity
As a result, the magnitude of the velocity is constant
However, the direction of the velocity changes
This means there is acceleration present in the circular motion, so there must be a net force
As it starts to move in a circle the tension of the string:
Continues to pull the puck at 90° to the linear velocity
Acts towards the centre of the circle
Is the only force acting on the puck
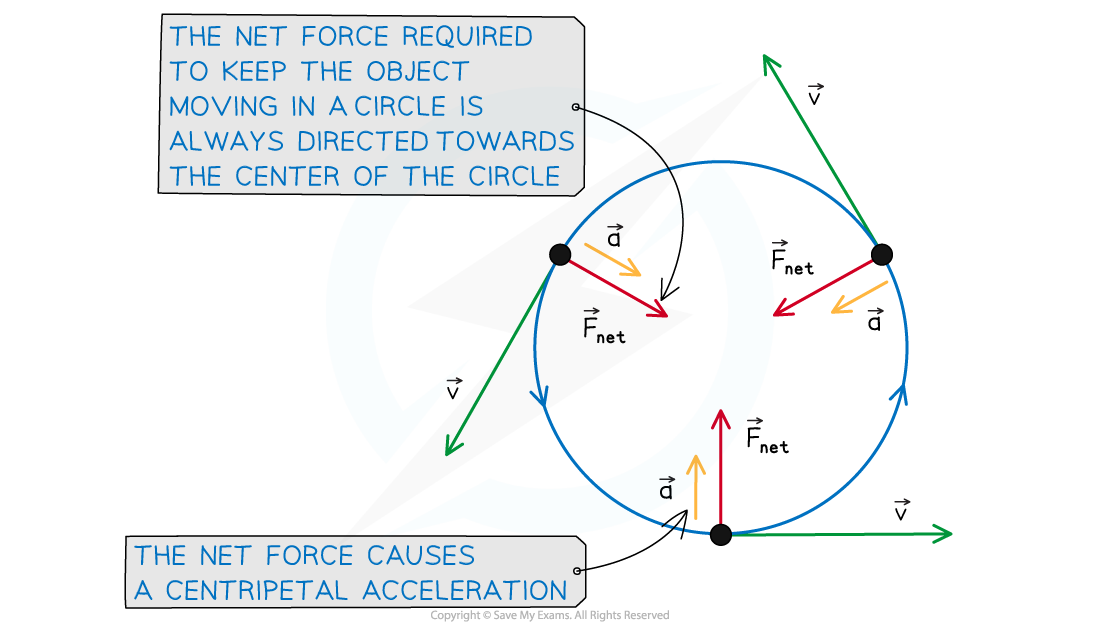
Hence, the net or overall force is towards the centre of the circle
So, the net force acting on the puck is called the centripetal force
Centripetal force and acceleration are always directed towards the centre of the circle
The centripetal force is not a separate force of its own
It can be any type of force, depending on the situation, which keeps an object moving in a circular path
Examples of centripetal force

Examiner Tips and Tricks
The term centripetal force should not be confused with "centrifugal force" as this is something that is thought to act away from the centre of a circle - this is the opposite of what is happening in circular motion
Centripetal Force
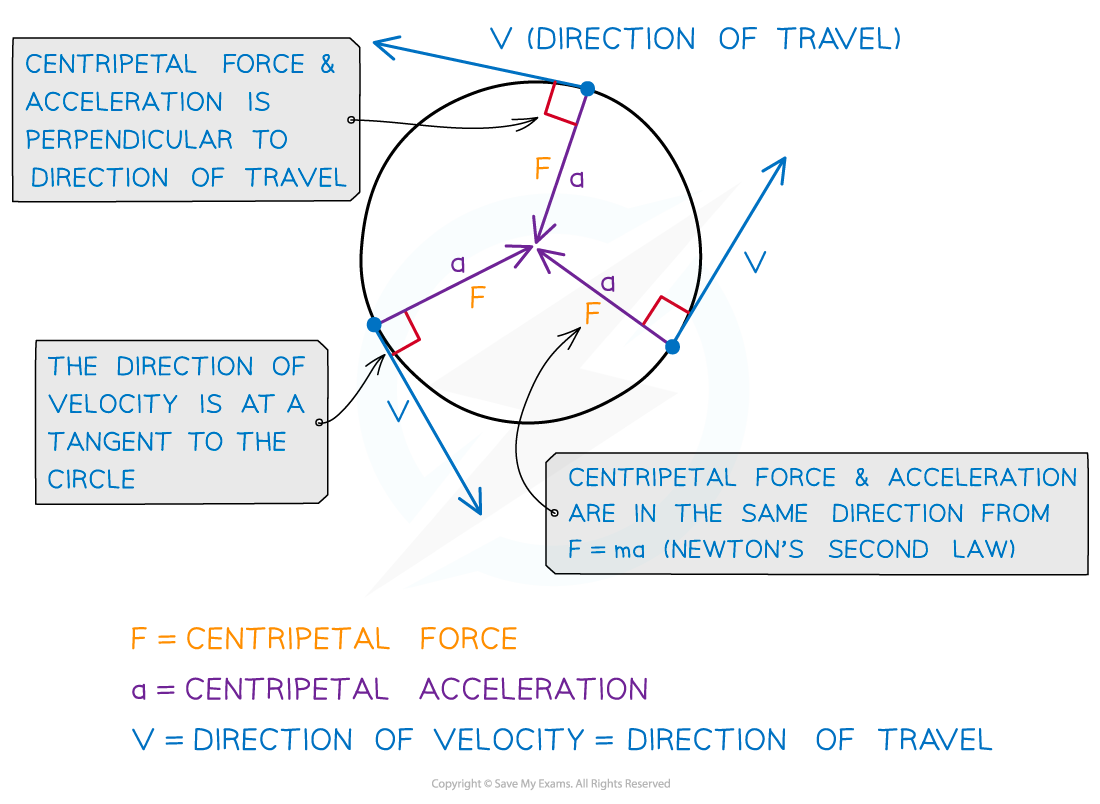
The centripetal force, F, is defined as:
The resultant force towards the centre of the circle required to keep a body in uniform circular motion. It is always directed towards the centre of the body's rotation.
Centripetal force can be calculated using:
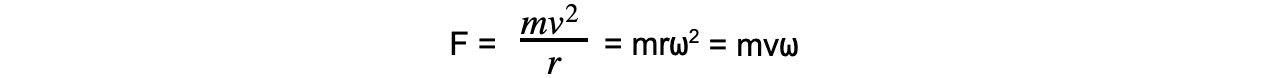
Centripetal force is always perpendicular to the direction of travel
Where:
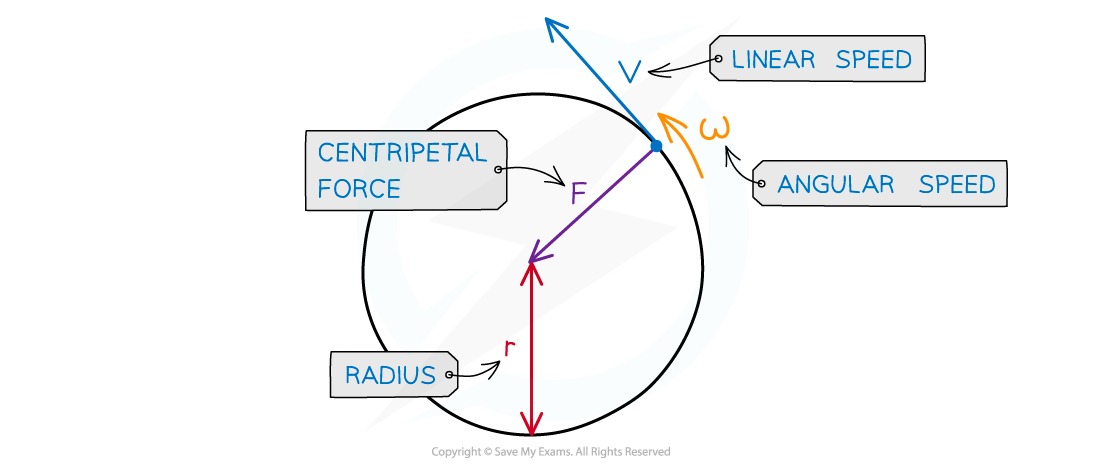
F = centripetal force (N)
v = linear velocity (m s-1)
⍵ = angular speed (rad s-1)
r = radius of the orbit (m)
Worked Example
A bucket of mass 8.0 kg is filled with water is attached to a string of length 0.5 m. What is the minimum speed the bucket must have at the top of the circle so no water spills out?

Answer:
Step 1: Draw the forces on the bucket at the top
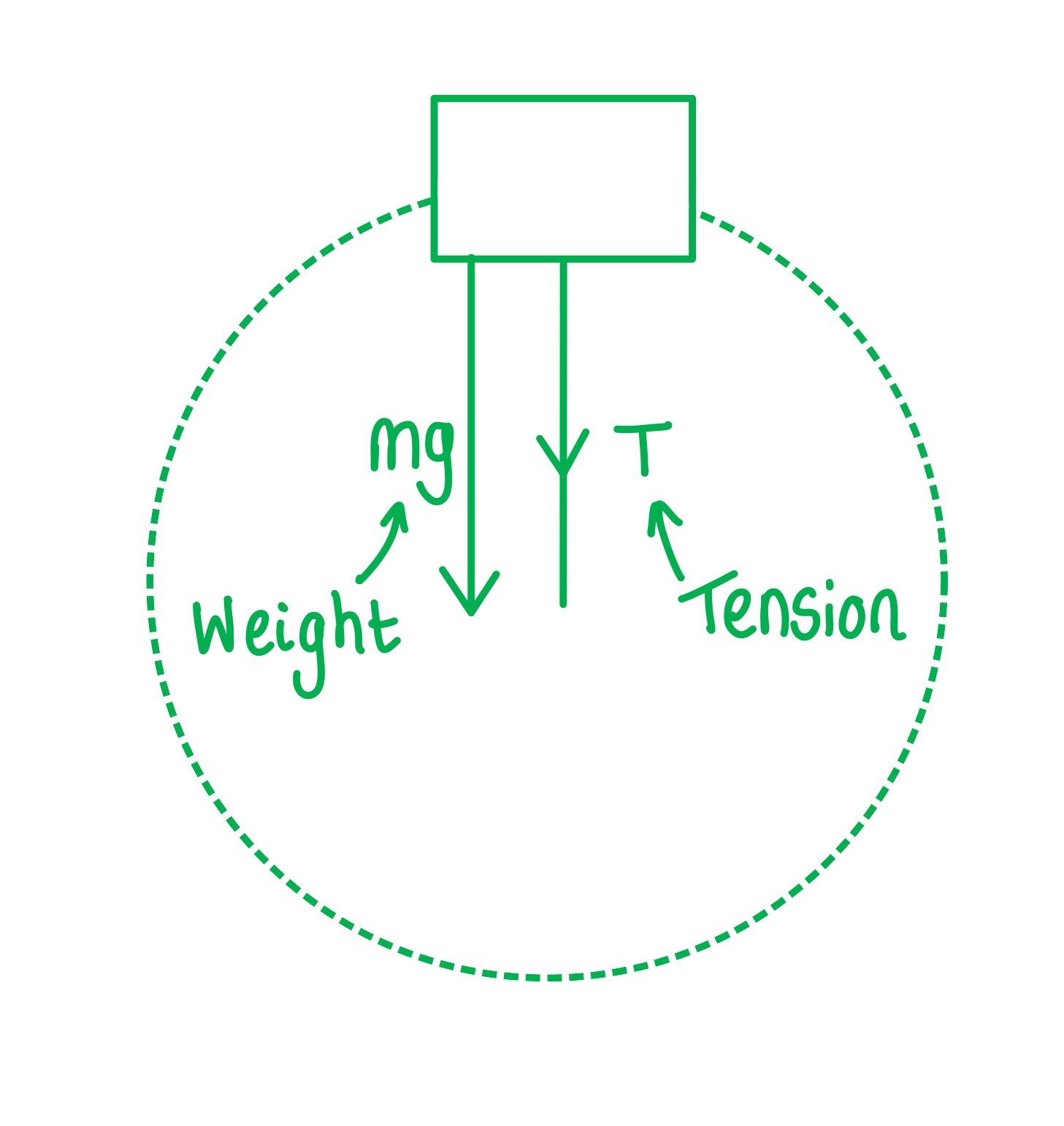
Step 2: Calculate the centripetal force
The weight of the bucket = mg
This is equal to the centripetal force since it is directed towards the centre of the circle

Step 3: Rearrange for velocity v
m cancels from both sides
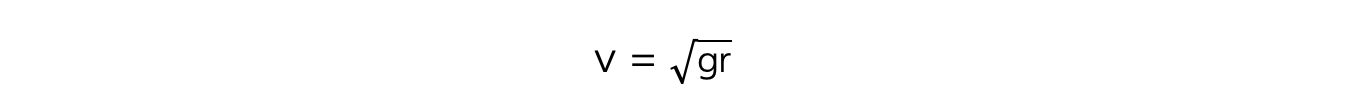
Step 4: Substitute in values
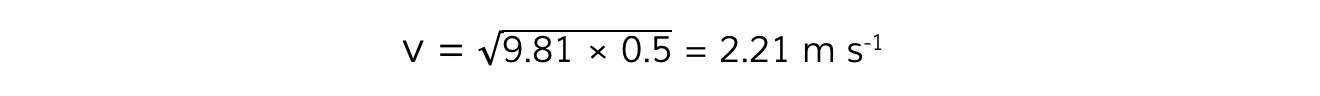

Unlock more, it's free!
Did this page help you?