A LevelPhysicsOCRRevision Notes5. Newtonian World & Astrophysics5.3 Kinetic Theory of Gases5.3.5 Internal Energy of an Ideal Gas

Internal Energy of an Ideal Gas (OCR A Level Physics)

Revision Note

Test yourself
Katie M

Author

Katie M

Last updated

Internal Energy of an Ideal Gas

  • The internal energy of a gas is defined as:

The sum of the kinetic and potential energies of the particles inside the gas

  • One of the assumptions of an ideal gas states: 
    • Electrostatic forces between particles in the gas are negligible except during collisions
    • So, there is no electrostatic potential energy in an ideal gas
  • All the internal energy is due to the kinetic energy of the particles

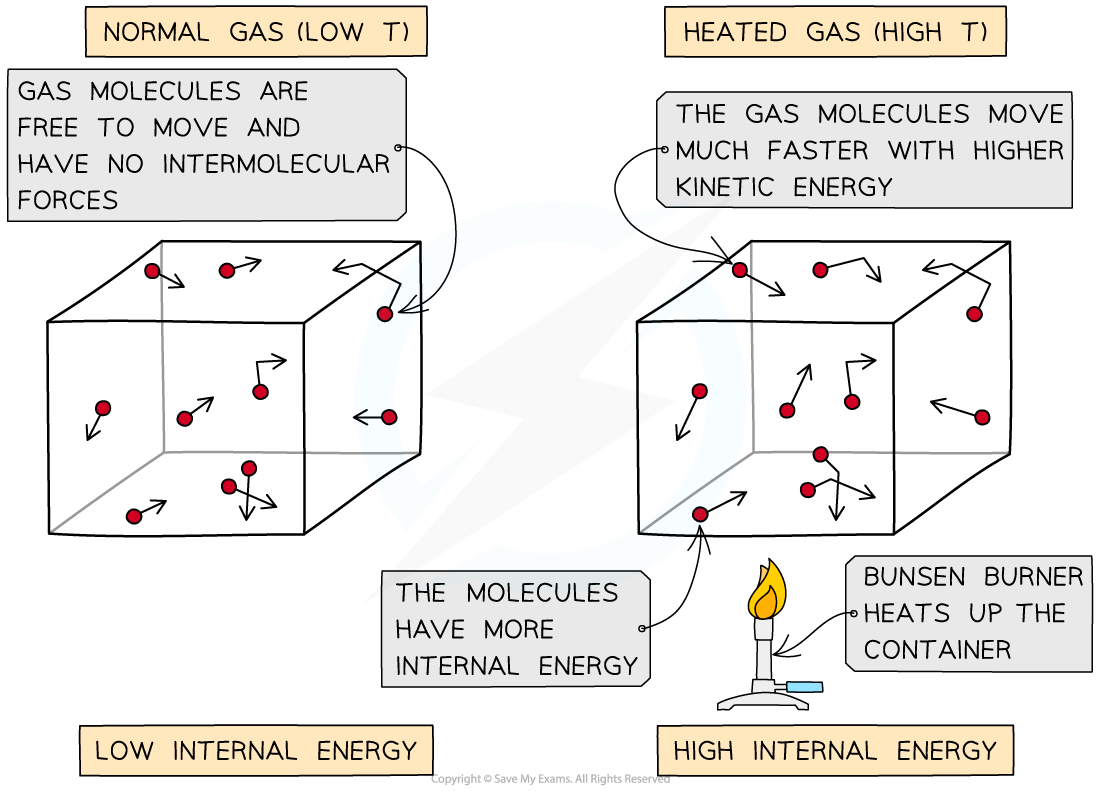
Change in internal energy, downloadable AS & A Level Physics revision notes

As the container is heated up, the gas molecules move faster with higher kinetic energy and therefore higher internal energy

  • Change in internal energy, ΔU is equal to the total kinetic energy, EK of all the particles 

bold increment bold italic U bold space bold equals bold italic E subscript bold K bold equals bold 1 over bold 2 bold italic N bold italic m stack bold c to the power of bold 2 with bold bar on top bold equals bold space bold 3 over bold 2 bold italic N bold italic k bold increment bold italic T

  • Where:
    • EK = total kinetic energy (J)
    • m = mass of one molecule (kg)
    • stack c squared with bar on top = mean square speed of a molecule (m2 s-2)
    • k = Boltzmann constant
    • T = temperature of the gas (K)
    • N = number of molecules
  • This equation shows that doubling the temperature will also double the internal energy of the particles

bold space bold space bold space bold space bold space bold space bold space bold space bold space bold space bold space bold space bold space bold space bold space bold space bold increment bold italic U bold space bold equals bold space bold 3 over bold 2 bold italic N bold italic k bold increment bold italic T bold 3 over bold 2 bold italic N bold italic k bold left parenthesis bold 2 bold italic T bold right parenthesis bold space bold equals bold space bold 6 over bold 2 bold italic N bold italic k bold italic T bold space bold equals bold space bold 3 bold italic N bold italic k bold italic T bold space bold equals bold space bold 2 bold italic U

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:5.3.4 Average Kinetic Energy of a MoleculeNext:5.4.1 Radians
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.