The Doppler Effect (OCR A Level Physics)

• If a wave source is stationary, the wavefronts spread out symmetrically
• If the wave source is moving, the waves can become squashed together or stretched out
• If the wave source is moving towards an observer the wavefronts will appear squashed
• If the wavefront is moving away from an observer the wavefronts will appear stretched out
• Therefore, when a wave source moves relative to an observer there will be a change in the observed frequency and wavelength

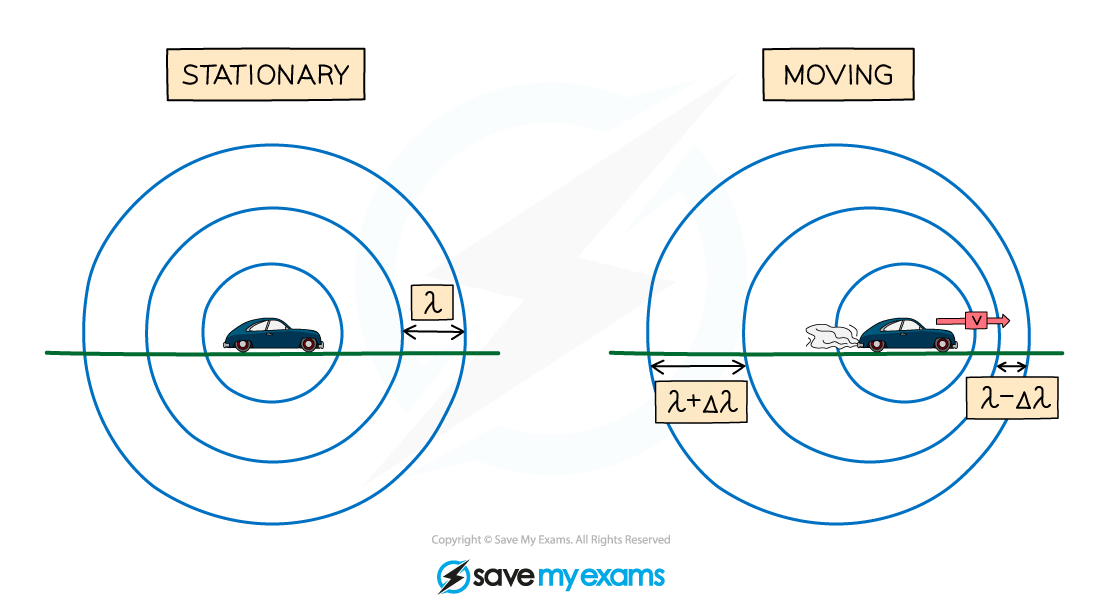
Wavefronts are even in a stationary object but are squashed in the direction of the moving wave source

• A moving object will cause the wavelength, λ, (and frequency) of the waves to change:
• The wavelength of the waves in front of the source decreases (λ – Δλ) and the frequency increases
• The wavelength behind the source increases (λ + Δλ) and the frequency decreases
• Note: Δλ means 'change in wavelength'
• The actual wavelength emitted by the source remains the same
• It is only the wavelength that is received by the observer that appears to have changed
• This effect is known as the Doppler effect or Doppler shift

• The Doppler effect is defined as:

      the apparent shift in wavelength occurring when the source of the waves is moving

• The Doppler effect, or Doppler shift, can be observed using any form of electromagnetic radiation
• It can be observed by comparing the light spectrum produced from a close object, such as our Sun, with that of a distant galaxy
  • The light from the distant galaxy is shifted towards the red end of the spectrum (There are more spectral lines in the red end)
  • This provides evidence that the universe is expanding

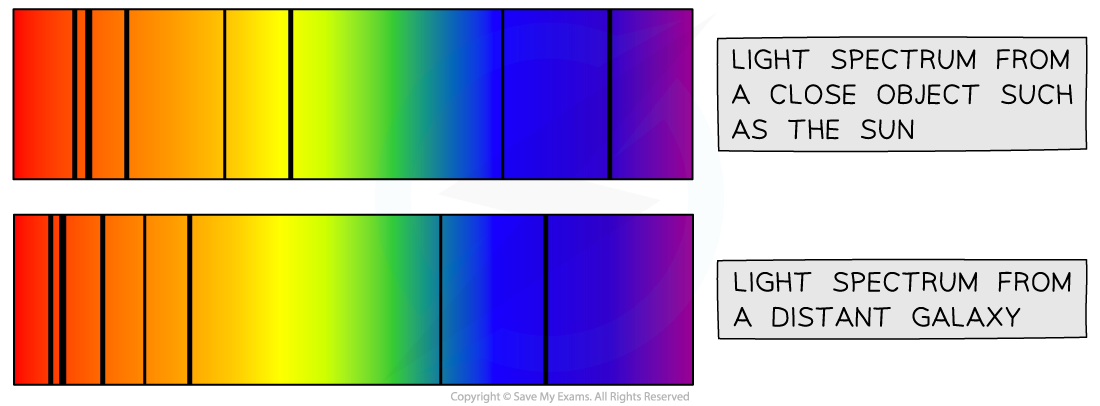
Comparing the light spectrum produced from the Sun and a distant galaxy

• Doppler shift (Doppler effect) describes how the wavelength (or frequency) of waves change when the source of the waves and observer are moving relative to each other
• If the relative speed between the source of the waves and the observer, ∆v, is small compared to the speed at which the wave is travelling, c, then the Doppler wavelength shift, ∆λ, and frequency shift, ∆f, is given by:

• Where: 
  • Δv = relative speed between source and observer (m s^–1)
  • c = speed of the wave (m s^–1)
  • Δf = observed change in frequency between moving source and stationary source of wave (Hz)
  • f = unshifted frequency of the wave emitted (Hz)
  • Δλ = observed change in wavelength between moving source and stationary source of wave (m)
  • λ = unshifted wavelength of the wave emitted (m)

 

• The relative speed between source and observer along the line joining them is give by:

∆v = v_s – v_o

• Where:
  • v_s = velocity of electromagnetic waves source
  • v_o = velocity of observer

• Usually, we are calculating the speed of the source of electromagnetic waves relative to an observer which we assume to be stationary
  • Therefore v_o = 0, hence ∆v = v_s = v
  • Where v is the velocity at which the source of the electromagnetic waves is moving from the observer

 

• Hence, the Doppler shift equation can therefore be written as:

   Step 1: List the known quantities

• • Unshifted wavelength = λ = 438 nm = 438 × 10^–9 m
  • Shifted wavelength = 608 nm = 608 × 10^–9 m
  • Change in wavelength = ∆λ = (608 – 438) × 10^–9 = 170 × 10^–9 m 
  • Speed of light = c = 3.00 × 10⁸ m s^–1

   Step 2: State the Doppler shift equation

   

   Step 3: Substitute values to calculate v

   v = =  = 1.16 × 10⁸ m s^–1