Gravitational Field Strength (OCR A Level Physics)

• There is a universal force of attraction between all matter with mass
  • This force is known as the ‘force due to gravity’ or the weight
• The Earth’s gravitational field is responsible for the weight of all objects on Earth

• The gravitational field strength g at a point is defined as force F per unit mass m of an object at that point:

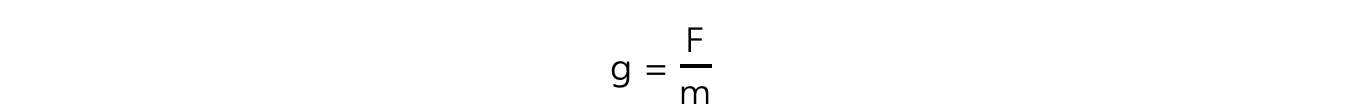
• Where:
  • g = gravitational field strength (N kg^–1)
  • F = force due to gravity, or weight (N)
  • m = mass (kg)

• This equation shows that:
  • The larger the mass of an object, the greater its pull on another mass
  • On planets with a large value of g, the gravitational force per unit mass is greater than on planets with a smaller value of g

• An object's mass remains the same at all points in space
  • However, on planets such as Jupiter, the weight of an object will be a lot greater than on a less massive planet, such as Earth
  • This means the gravitational force would be so high that humans, for example, would not be able to fully stand up (or, even worse...)

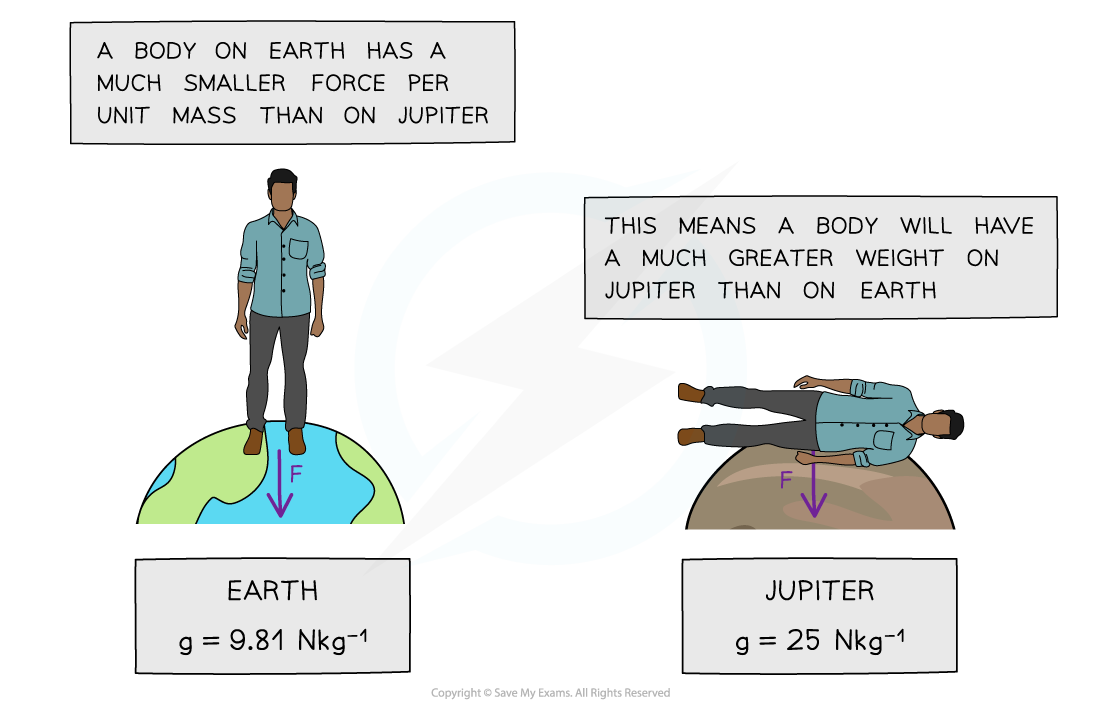
The weight force on Jupiter would be so large that even standing upright would be difficult

• Factors that affect the gravitational field strength at the surface of a planet are:
  • The radius (or diameter) of the planet
  • The mass (or density) of the planet

• In a radial field (due to a point mass M), the gravitational field lines get further apart from each other
  • This indicates that the strength of the gravitational field decreases with distance from the centre of mass of M

• The gravitational field strength g in a radial field, due to some mass M, is given by the equation:

• Where: 
  • g = gravitational field strength (N kg^–1)
  • G = Newton's Gravitational constant (N m² kg^–2)
  • M = mass of the object causing the gravitational field (kg)
  • r = radial distance from the centre of mass of M (m)

• Note:
  • The negative sign in this equation indicates that the gravitational field is attractive
  • In other words, the direction of the gravitational field lines is towards the mass M

• On the Earth’s surface, g has a constant value of 9.81 N kg^-1
• However far outside the Earth’s surface, g is not constant
  • g decreases as r increases by a factor of 1/r²
  • This is an inverse square law relationship with distance

• When the magnitude of g is plotted against the distance from the centre of a planet, r has two parts:
  • When r < R (the radius of the planet), g is directly proportional to r
  • When r > R, g is inversely proportional to r² 

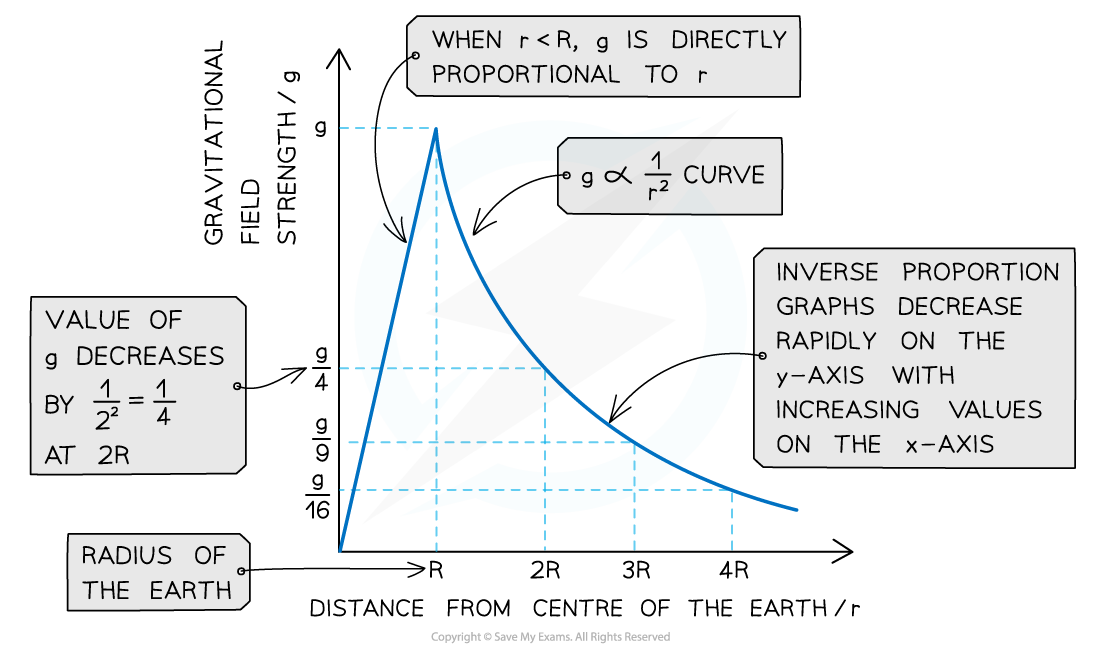
The magnitude of gravitational field strength g against distance r from the Earth's surface follows a 1/r² relationship

• Near the Earth's surface, the gravitational field is uniform
  • Hence, the gravitational field lines are parallel and evenly spaced

• This means the gravitational field strength is constant at every point near the Earth's surface
  • Numerically, the gravitational field strength near Earth's surface is equal to the acceleration due to gravity, g = 9.81 m s^–2 

Step 1: Write the known quantities

• • Radius of the Earth R_E = 6400 km = 6400 × 10³ m
  • Mass of the earth M_E = 6.0 × 10²⁴ kg
  • Gravitational constant G = 6.67 × 10^–11 N m² kg^–2

Step 2: Recall the value of the gravitational field strength at the Earth's surface

• • The gravitational field strength at the Earth's surface g = 9.81 N kg^–1

Step 3: Write the equation for gravitational field strength in a radial field

• • The Earth creates a radial gravitational field (far from its surface) therefore the equation for gravitational field strength g is: 

Step 4: Determine the distance r at which the field strength reduces by a factor of 0.5

• • If the field strength decreases by a factor of 0.5, then g × 0.5 = 9.81 × 0.5 = 4.905 N kg^–1
  • Therefore, ignoring the negative sign (as we only want a magnitude): 

4.905 = 

r² = 

r = = 9.0 × 10⁶ m

Step 5: Determine the distance from the Earth's surface

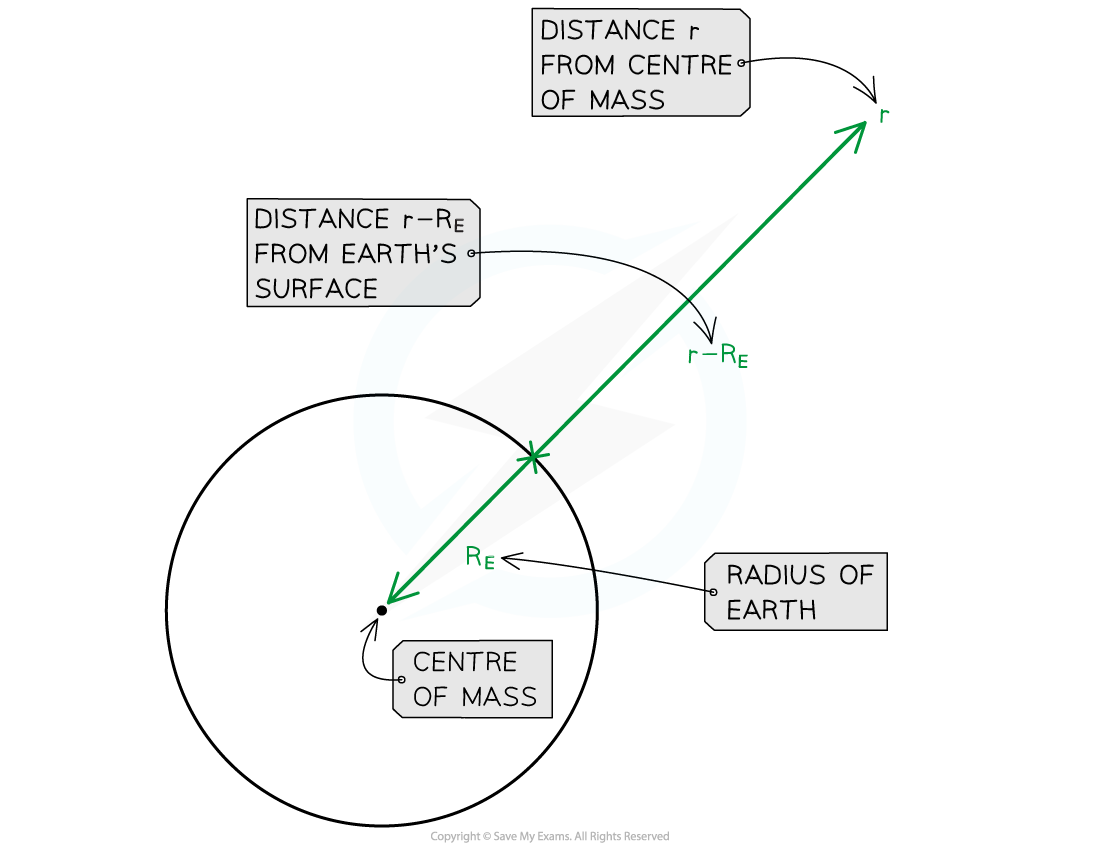
• • The value r = 9.0 × 10⁶ m is the radial distance from the Earth's centre of mass
  • Therefore, the gravitational field strength reduces by a factor 0.5 at a distance r – R_E

r – R_E = (9.0 × 10⁶) – (6400 × 10³) = 2.6 × 10⁶ m