Stellar Parallax (OCR A Level Physics)

Stellar Parallax

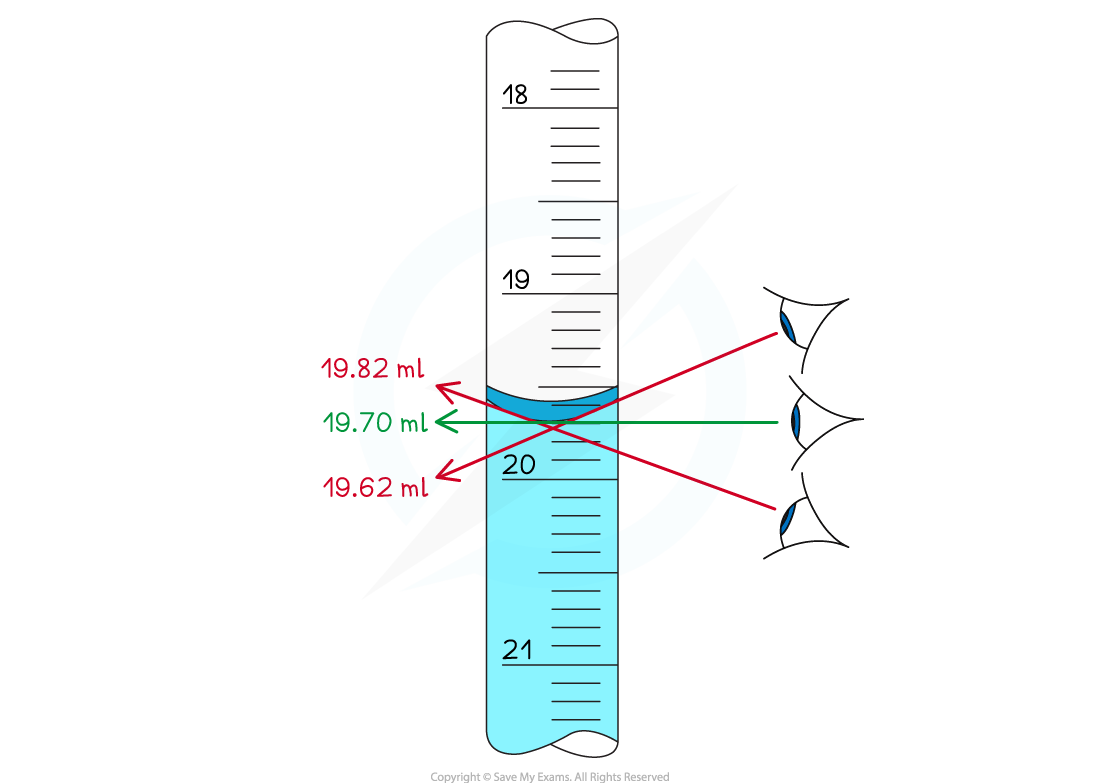
• The principle of parallax is based on how the position of an object appears to change depending on where it is observed from

  • When observing the volume of liquid in a measuring cylinder the parallax principle will result in the observer obtaining different values based on where they viewed the bottom of the meniscus from

• Stellar parallax can be used to measure the distance to nearby stars

• Stellar Parallax is defined as:

  The apparent shifting in position of a nearby star against a background of distant stars when viewed from different positions of the Earth, during the Earth’s orbit about the Sun

• It involves observing how the position of a nearby star changes over a period of time against a fixed background of distant stars

  • To an observer the position of distant stars does not change with time

• If a nearby star is viewed from the Earth in January and again in July, when the Earth is at a different position in its orbit around the Sun, the star will appear in different positions against a backdrop of distant stars which will appear to not have moved

• This apparent movement of the nearby star is called the stellar parallax

The Parallax Equation

• Applying trigonometry to the parallax equation:

  • 1 AU = radius of Earths orbit around the sun

  • p = parallax angle from earth to the nearby star

  • d = distance to the nearby star

  • So, tan(p) = 

• For small angles, expressed in radians, tan(p) ≈ p, therefore: p = 

• If the distance to the nearby star is to be measured in parsec, then it can be shown that the relationship between the distance to a star from Earth and the angle of stellar parallax is given by

• Where:

  • p = parallax (")

  • d = the distance to the nearby star (pc)

• This equation is accurate for distances of up to 100 pc

  • For distances larger than 100 pc the angles involved are so small they are hard to measure accurately