Interference (OCR A Level Physics) : Revision Note
Interference
Interference occurs when waves overlap and their resultant displacement is the sum of the displacement of each wave
This result is based on the principle of superposition
The resultant waves may be smaller or larger than either of the two individual waves
When two waves with the same frequency and amplitude arrive at a point, they superpose either:
In phase, causing constructive interference. The peaks and troughs line up on both waves and the resultant wave has double the amplitude
In anti-phase, causing destructive interference. The peaks on one wave line up with the troughs of the other. The resultant wave has no amplitude
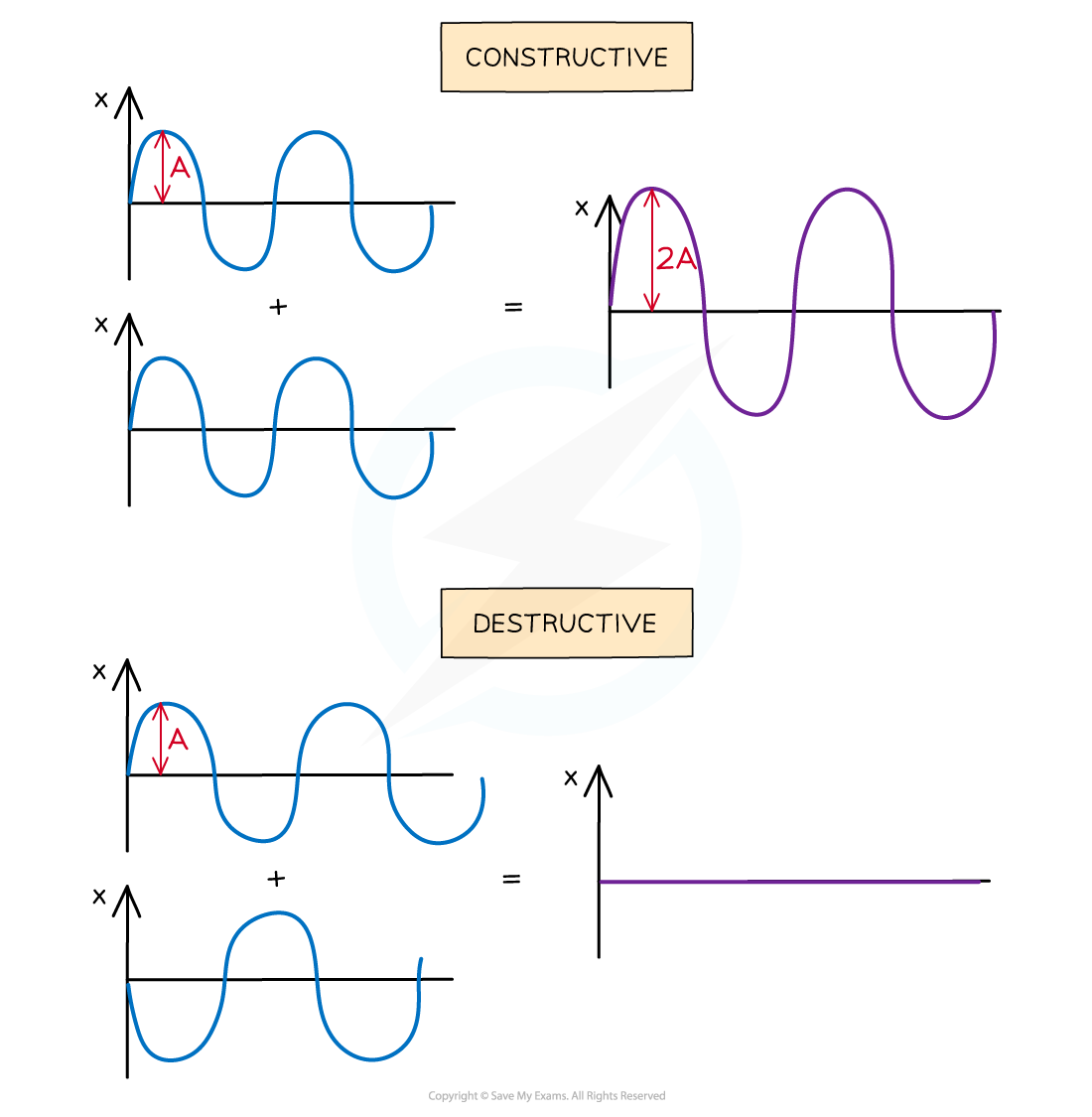
Waves in superposition can undergo constructive or destructive interference
The principle of superposition applies to all types of waves i.e. transverse and longitudinal, progressive and stationary
Coherence
At points where the two waves are neither in phase nor in antiphase, the resultant amplitude is somewhere in between the two extremes
Waves are said to be coherent if they have:
The same frequency
A constant phase difference
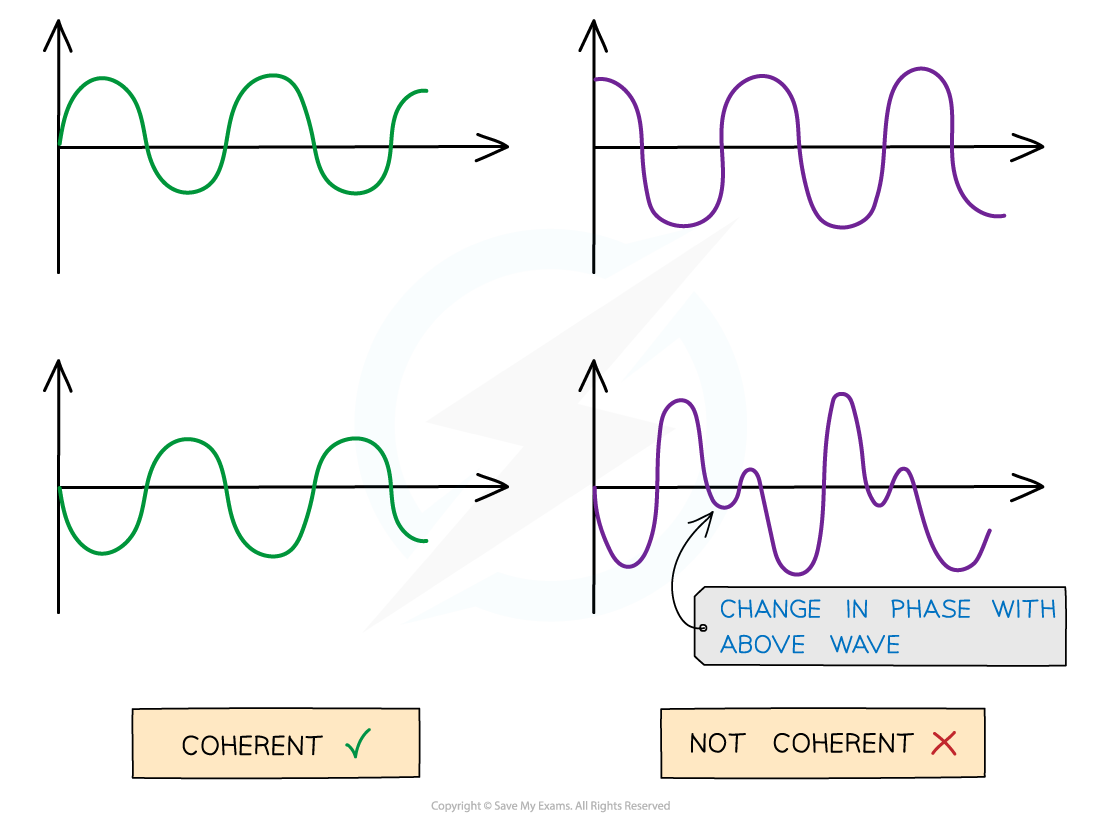
Coherent v non-coherent wave. The abrupt change in phase creates an inconsistent phase difference
Coherence is vital in order to produce an observable, or hearable, interference pattern
Laser light is an example of a coherent light source, whereas filament lamps produce incoherent light waves
When coherent sound waves are in phase, the sound is louder because of constructive interference
Path Difference
Path difference is defined as:
The difference in distance travelled by two waves from their sources to the point where they meet
Path difference is generally expressed in multiples of a wavelength
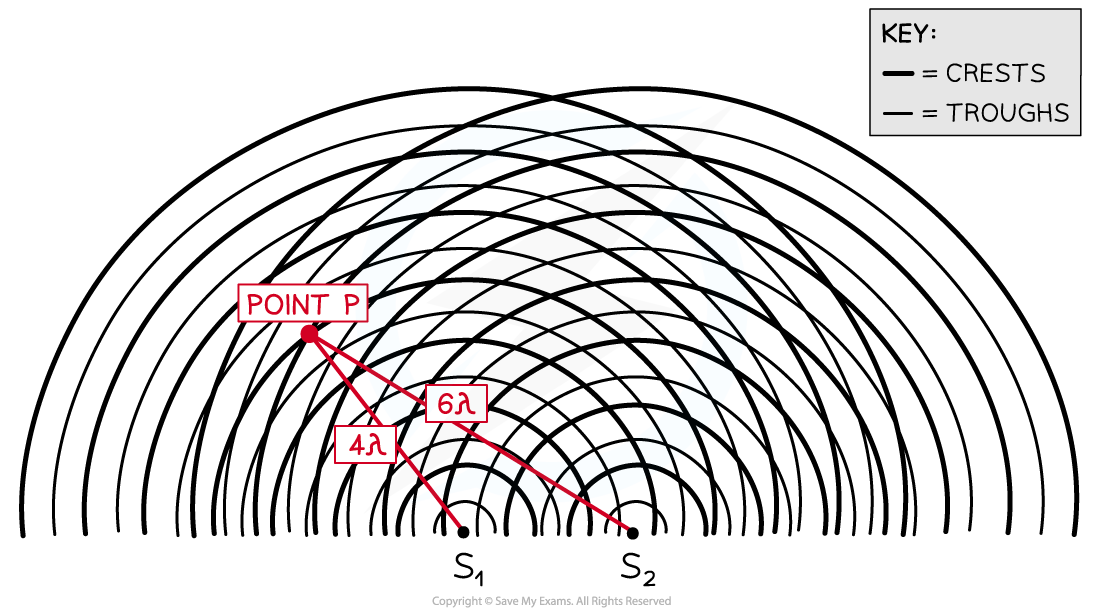
At point P the waves have a path difference of a whole number of wavelengths resulting in constructive interference
Another way to represent waves spreading out from two sources is shown in the diagram above
At point P, the number of crests from:
Source S1 = 4λ
Source S2 = 6λ
The path difference at P is 6λ – 4λ = 2λ
Phase Difference
Two waves with a path difference will also have a difference in phase
This is their phase difference
Phase difference is defined as:
The difference in phase between two waves that arrive at the same point
It is given as an angle, in radians or degrees
Examiner Tips and Tricks
Think of ‘constructive’ interference as ‘building’ the wave and ‘destructive’ interference as ‘destroying’ the wave.
Constructive & Destructive Interference
Whether two waves will constructively or destructively interfere at a point is determined by its path difference or phase difference
Path Difference
Path difference is determined in multiples of a wavelength
Constructive interference occurs when there is a path difference of nλ
For example, 2λ
Destructive interference occurs when there is a path difference of (n + ½)λ
For example, 3λ / 2 or 1.5λ
In this case, n is an integer i.e. 1, 2, 3...
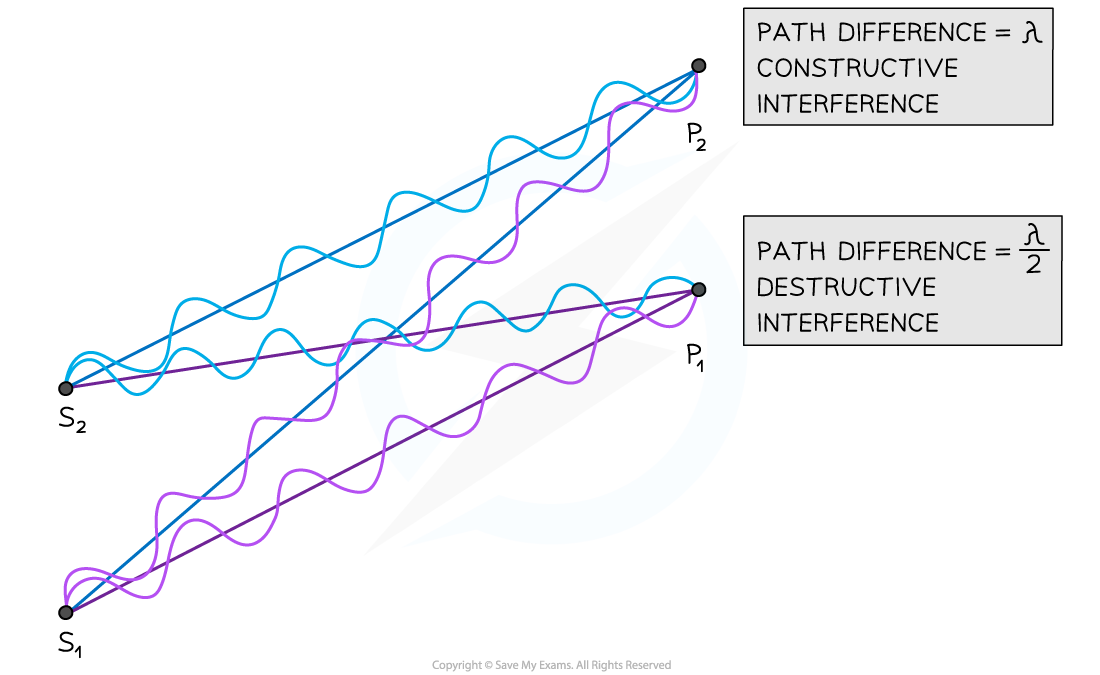
At point P2 the waves have a path difference of a whole number of wavelengths resulting in constructive interference. At point P1 the waves have a path difference of an odd number of half wavelengths resulting in destructive interference
In the diagram above, the number of wavelengths between:
S1 ➜ P1 = 6λ
S2 ➜ P1 = 6.5λ
S1 ➜ P2 = 7λ
S2 ➜ P2 = 6λ
The path difference at point P1 is 6.5λ – 6λ = λ / 2
Therefore, this is destructive interference (half-wavelength difference)
The path difference at point P2 is 7λ – 6λ = λ
Therefore, this is constructive interference (a whole number of wavelengths difference)
Phase Difference
The phase difference between two waves is determined by an angle, in radians or degrees
Constructive interference occurs when the phase difference is an even multiple of π or that they are in phase
Eg. 2π, 4π
Destructive interference occurs when the phase difference is an odd multiple of π or that they are in anti-phase
Eg. π, 3π
Worked Example
The diagram shows the interferences of coherent waves from two point sources.
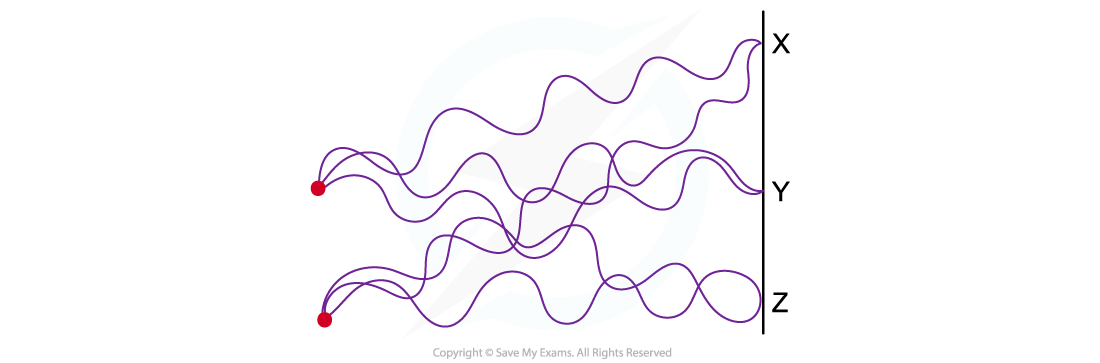
Which row in the table correctly identifies the type of interference at points X, Y and Z.
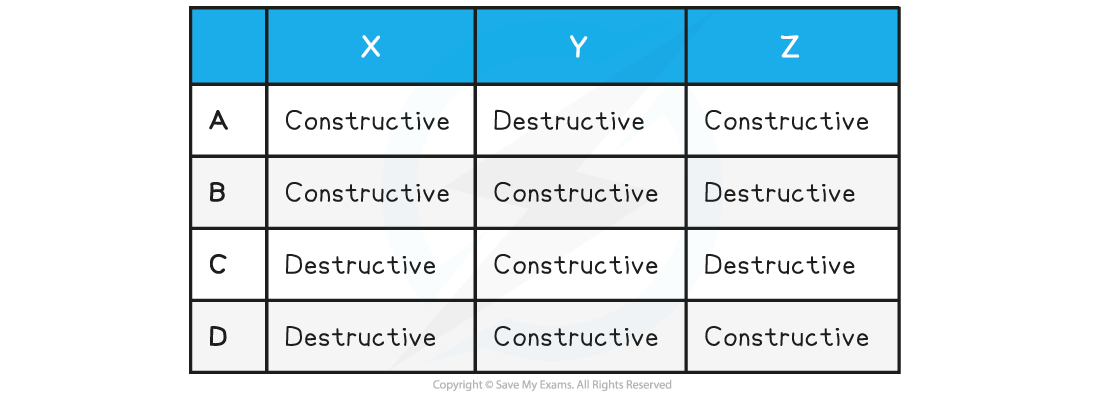
Answer: B
At point X:
Both peaks of the waves are overlapping
Path difference = 5.5λ – 4.5λ = λ
This is constructive interference and rules out options C and D
At point Y:
Both troughs are overlapping
Path difference = 3.5λ – 3.5λ = 0
Therefore constructive interference occurs
At point Z:
A peak of one of the waves meets the trough of the other
Path difference = 4λ – 3.5λ = λ / 2
This is destructive interference
Examiner Tips and Tricks
Remember, interference of two waves can either be:
In phase, causing constructive interference
The peaks and troughs line up on both waves
The resultant wave has double the amplitude
In anti-phase, causing destructive interference
The peaks on one wave line up with the troughs of the other
The resultant wave has no amplitude

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
