Refraction (OCR A Level Physics) : Revision Note
Refraction
Refraction occurs when light passes a boundary between two different transparent media
At the boundary, the rays of light undergo a change in direction
The direction is taken as the angle from a hypothetical line called the normal
This is perpendicular to the surface of the boundaries and is represented by a straight dotted line
The change in direction depends on which media the light rays pass between:
From air to glass (less dense to more dense): light bends towards the normal
From glass to air (more dense to less dense): light bends away from the normal
When passing along the normal (perpendicular) the light does not bend at all
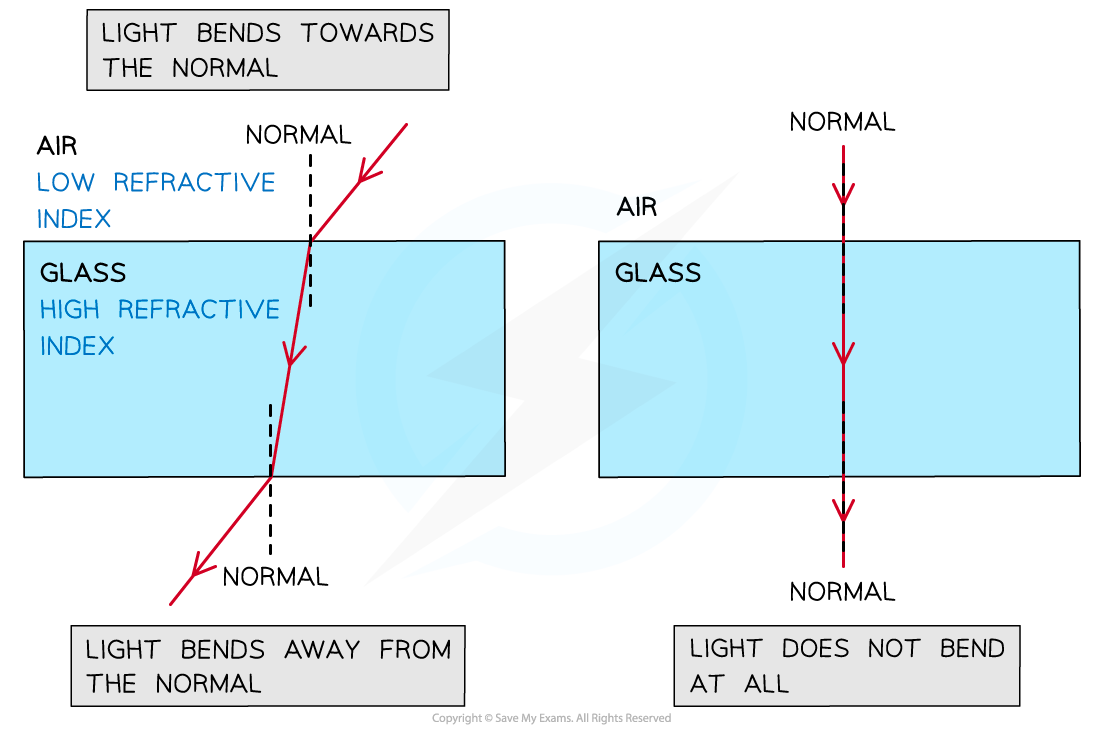
Refraction of light through a glass block
The change in direction occurs due to the change in speed when travelling in different substances
When light passes into a denser substance the rays will slow down, hence they bend towards the normal
The only properties that change during refraction are speed and wavelength – the frequency of waves does not change
Calculating Refractive Index
The refractive index, n, is a property of a material which measures how much light slows down when passing through it
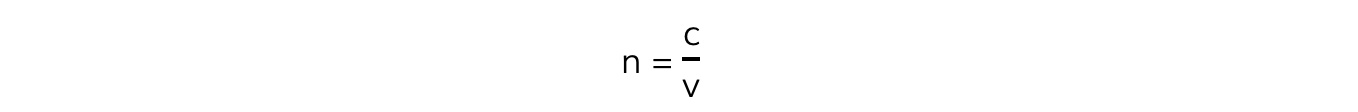
Where:
c = the speed of light in a vacuum (m s–1)
v = the speed of light in a substance (m s–1)
Light travels at different speeds within different substances depending on their refractive index
A material with a high refractive index is called optically dense, such material causes light to travel slower
Since the speed of light in a substance will always be less than the speed of light in a vacuum, the value of the n is always greater than 1
In calculations, the refractive index of air can be taken to be approximately 1
This is because light does not slow down significantly when travelling through air (as opposed to travelling through a vacuum)
Snell's Law
Snell’s law relates the angle of incidence to the angle of refraction, it is given by:
n1 sin θ1 = n2 sin θ2
Where:
n1 = the refractive index of material 1
n2 = the refractive index of material 2
θ1 = the angle of incidence of the ray in material 1
θ2 = the angle of refraction of the ray in material 2
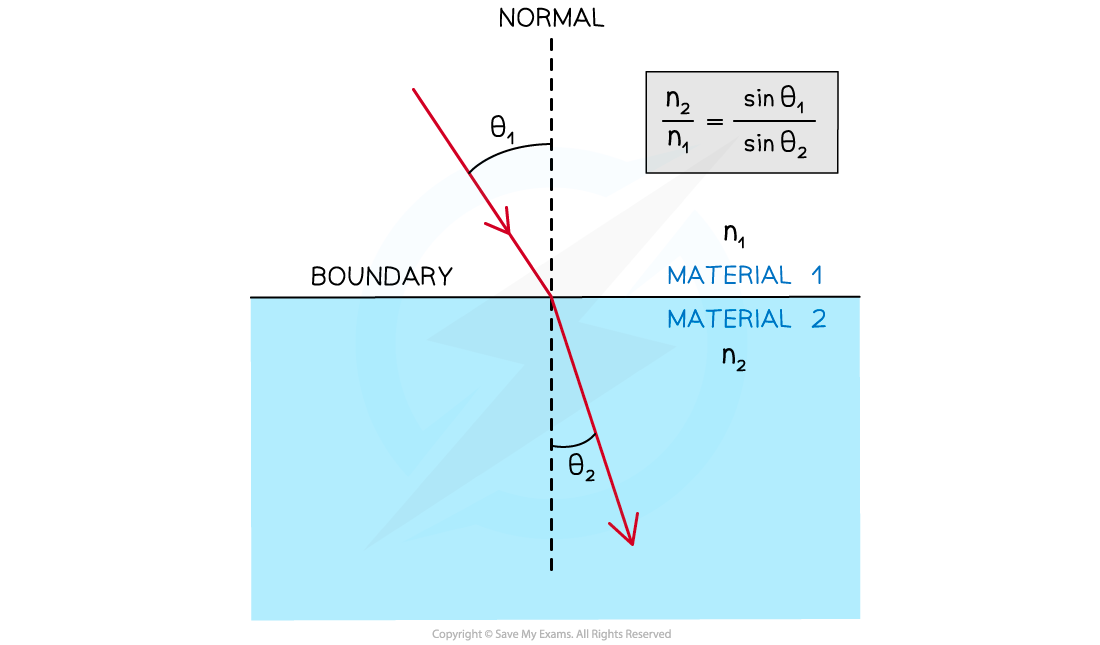
Snell's Law is used to find the refractive indices or the angles to the normal at a boundary
θ1 and θ2 are always taken from the normal
Material 1 is always the material in which the ray goes through first
Material 2 is always the material in which the ray goes through second
Worked Example
A light ray is directed at a vertical face of a glass cube. The angle of incidence at the vertical face is 39° and the angle of refraction is 25° as shown in the diagram.
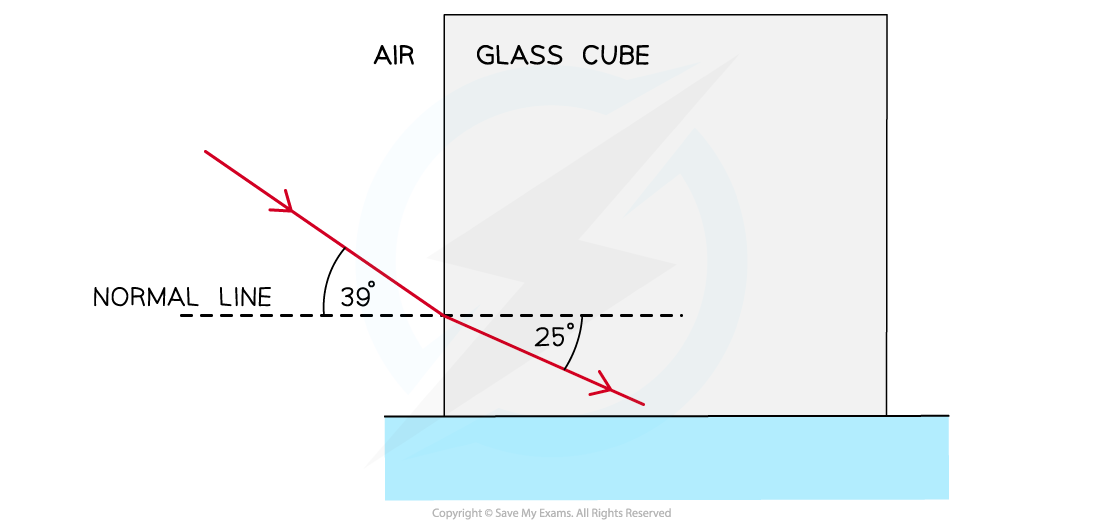
Show that the refractive index of the glass is about 1.5.
Answer:


Examiner Tips and Tricks
Always double-check if your calculations for the refractive index are greater than 1. Otherwise, something has definitely gone wrong in your calculation!The refractive index of air will not be given in the question. Always assume that nair = 1.Always check that the angle of incidence and refraction are the angles between the normal and the light ray. If the angle between the light ray and the boundary is calculated instead, calculate 90 – θ (since the normal is perpendicular to the boundary) to get the correct angle.
Investigating Refraction & Total Internal Reflection
Aims of the Experiment
The aim of the experiment is to calculate the refractive index of a transparent semi-circular block
Variables:
Independent variable = Angle of incidence, θ1
Dependent variable = Angle of refraction, θ2
Control variables:
Size of the semi-circular block
Intensity of light
Equipment List

Resolution of measuring equipment:
Ruler = 1 mm
Protractor = 1°
Method
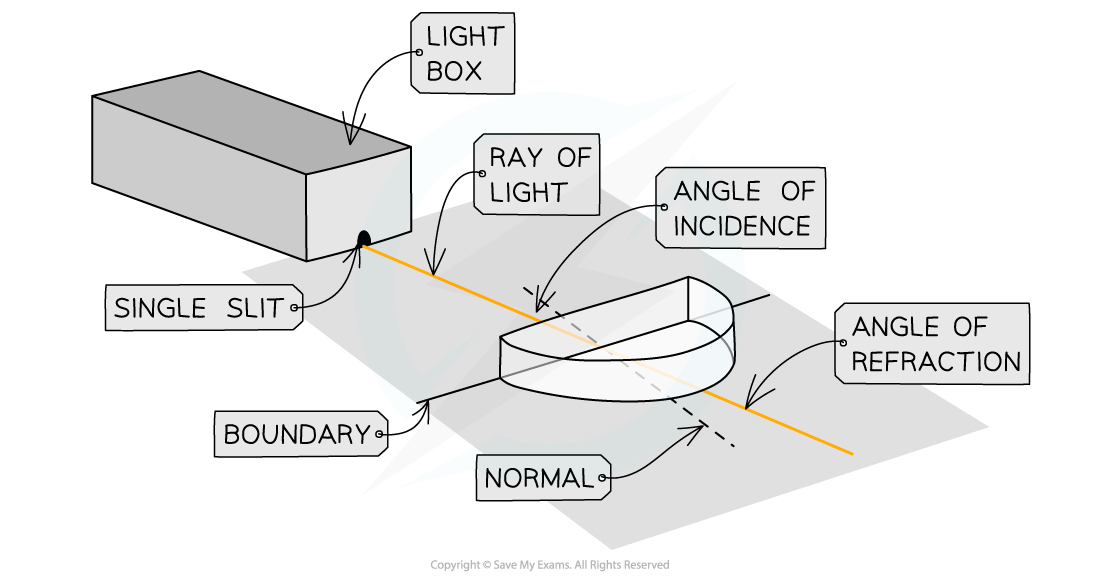
Apparatus set up to measure the effects of refraction through a semi-circular block
Place the semi-circular block on top of the protractor with the centre of its diameter aligned with 0° on the protractor
Direct the light from the lightbox towards this 0° and draw a dotted line perpendicular to the long edge of the semi-circular block. This is the normal
Using the pencil and ruler, trace the ray entering the block and leaving
Repeat this, moving the ray around every 10° up to 80. This is the angle of incidence, θ1
The angle of the ray leaving the block from the normal is the angle of refraction, θ2. The block should preferably be removed to measure this accurately
Record the angle at which the angle of refraction is 90°, (the ray leaves along the straight boundary of the block) just before it is reflected. This is the critical angle
Repeat the experiment for the rectangular glass block
An example table of results would look like this:
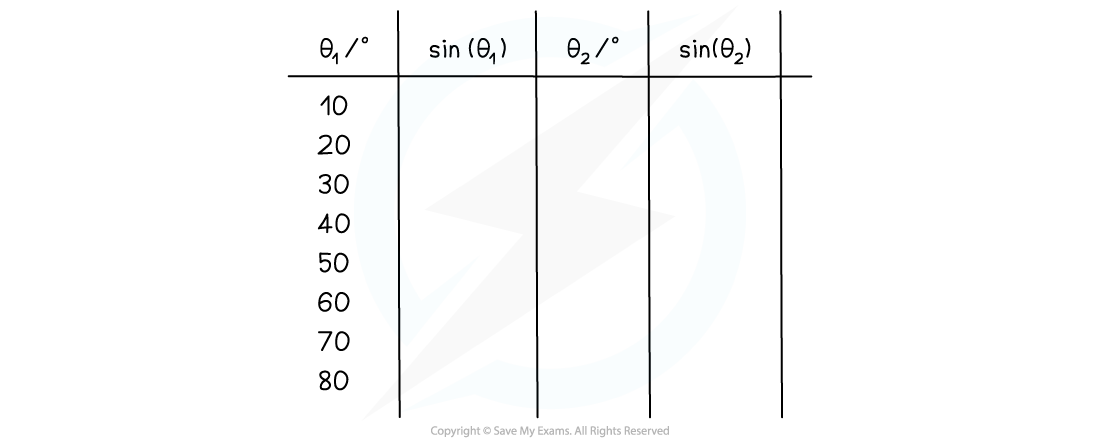
Example table of results
Analysis of Results
The refractive index of the blocks is calculated using Snell's Law:
n1 sin θ1 = n2 sin θ2
Since n1 is the refractive index of the first material, this is air and hence equal to 1
Therefore, the refractive index of the blocks n is found using the equation:
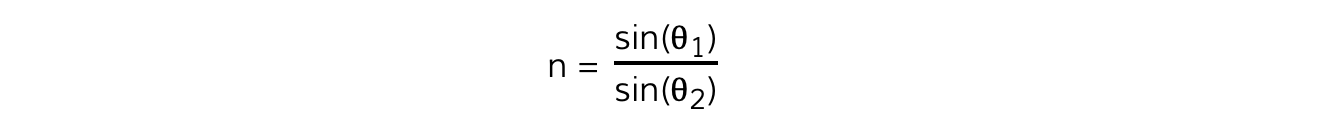
Therefore the gradient of the graph of sin θ2 against sin θ1 is the refractive index n
The critical angle, C, can then be calculated using the equation
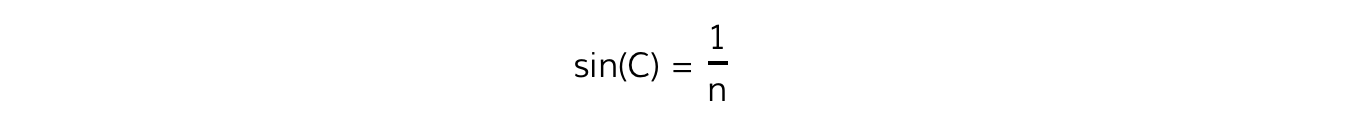

Example graph of results to measure the refractive index
Evaluating the Experiment
Systematic Errors:
The lines should be traced from the centre of the light rays each time
Random Errors:
Use a pencil with a sharp tip to draw the lines on the paper accurately for each angle
The light from the lightbox will be slightly blurry and dispersed, which gives a subjective reading for the angle
Using a concentrate laser light will produce more defined rays so there is less uncertainty when tracing the lines
Repeat the experiment and find an average reading of each angle of refraction
Safety Considerations
Do not shine the light from the ray box in eyes as it can damage your eyes
Lasers can permanently damage your eyesight therefore, wear laser safety goggles
Don’t shine the laser at reflective surfaces
Display a laser warning sign on the door
Never shine the laser at a person
Make sure the glass blocks are kept away from the edge of the surface of a table, as they could be damaged and crack if they fall

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
