Energy Transfer (OCR A Level Physics) : Revision Note
Energy Transfer in Circuits
E.m.f is defined as the energy transferred by the power supply per unit charge
This energy transformed is also equal to the work done by the moving charge
This is defined by the equation:
W = εQ
Where:
W = work done / energy transferred (J)
ε = e.m.f (V)
Q = charge (C)
The potential difference is the energy transferred to the electrical component per unit charge
This means the equation can also be written as:
W = VQ
Where:
V = potential difference (V)
These equations show that
1 V = 1 J C-1
Worked Example
An electric kettle requires 0.4 MJ to be supplied to boil a cup of water. The e.m.f. of the mains supply is 230 V.Calculate the charge supplied.
Answer:
Step 1: List the known quantities
Energy transferred (work done), W = 0.4 MJ = 0.4 × 106 J
E.m.f, ε = 230 V
Step 2: Write the relevant equation
W = εQ
Step 3: Rearrange for charge, Q
Q = W ÷ ε
Step 4: Substitute in the values
Q = (0.4 × 106) ÷ 230 = 1739.13 = 1700 C
Energy Transfer for Charged Particles
A dynamo or battery transfer energy to each charge carrier, which are electrons in metals, as they pass through
Each electron has a charge of e
Since the energy transferred (work done) W is defined as
W = QV
Then:
W = eV
Where the charge Q is now replaced with the charge of the electron e
1 eV is 1 electronvolt, which is defined as:
A unit of energy equal to the work done by an electron accelerated through a potential difference of 1 volt
When a potential difference is applied across a conductor, the electrons are accelerated and gain kinetic energy
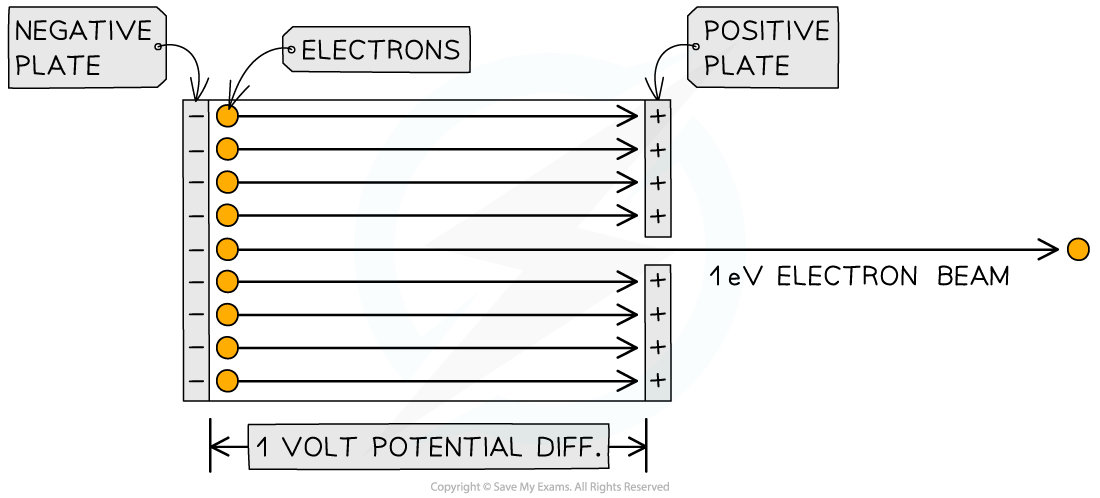
Electron beam accelerated through a potential difference of 1 V
This kinetic energy gained is equal to an electronvolt:
eV = ½ mv2
Where:
e = elementary charge (C)
V = potential difference (V)
m = mass of the electron (kg)
v = speed of the electrons (m s-1)
To convert between eV and J:
eV → J: multiply by 1.6 × 10-19
J → eV: divide by 1.6 × 10-19
Worked Example
Calculate the speed of an electron that is accelerated through a potential difference of 5 V.
Answer:

Examiner Tips and Tricks
Remember to clearly state the difference between lower case v meaning velocity and upper case V meaning the potential difference in your exam, otherwise, you may define or substitute the wrong value!

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
