Young Double-Slit Experiment (OCR A Level Physics) : Revision Note
Young Double-Slit Experiment
For two-source interference fringes to be observed, the sources of the wave must be:
Coherent (constant phase difference)
Monochromatic (single wavelength)
When two waves interfere, the resultant wave depends on the phase difference between the two waves
This is proportional to the path difference between the waves which can be written in terms of the wavelength λ of the wave
As seen from the diagram, the wave from slit S2 has to travel slightly further than that from S1 to reach the same point on the screen
The difference in this distance is the path difference
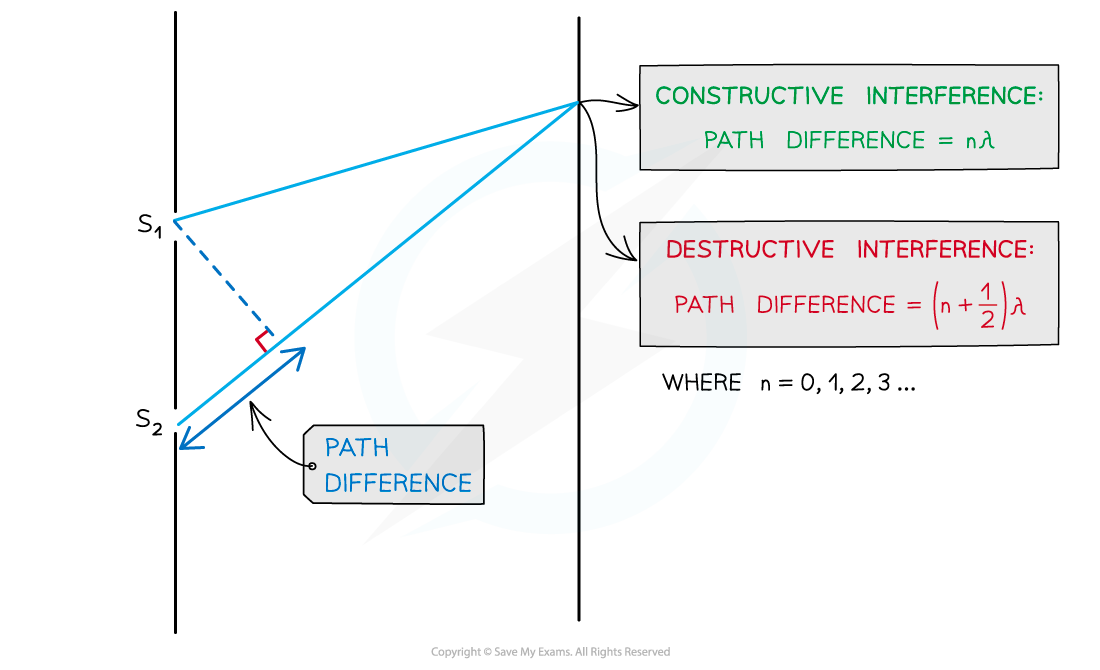
Path difference of constructive and destructive interference is determined by wavelength
For constructive interference (or maxima), the difference in wavelengths will be an integer number of whole wavelengths
For destructive interference (or minima) it will be an integer number of whole wavelengths plus a half wavelength
n is the order of the maxima/minima since there is usually more than one of these produced by the interference pattern
An example of the orders of maxima is shown below:
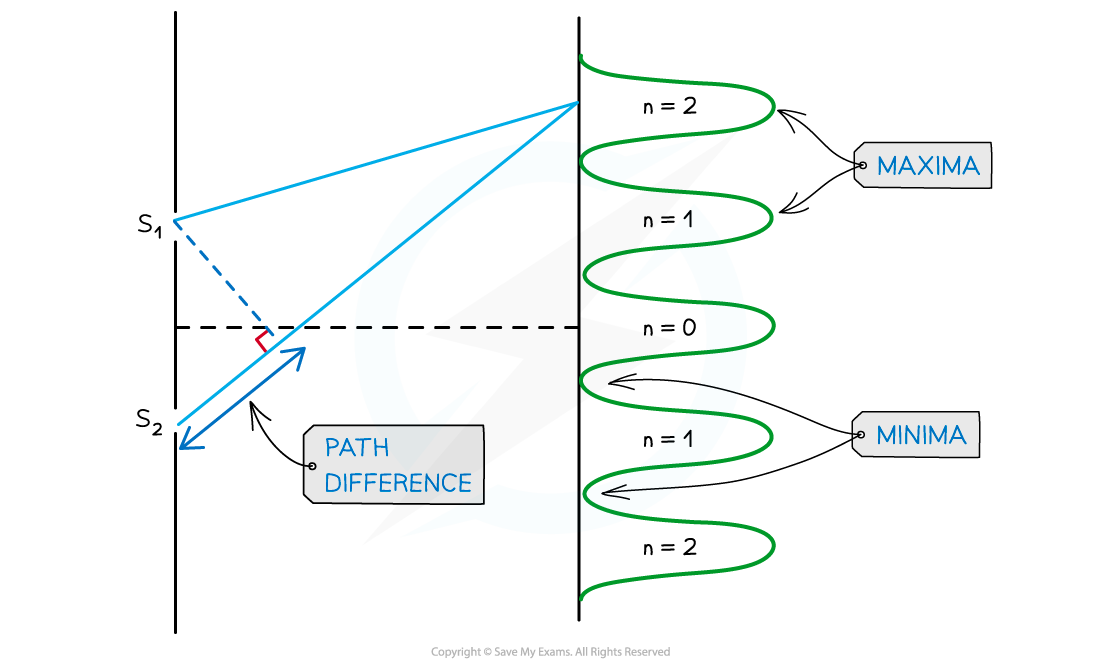
Interference pattern of light waves shown with orders of maxima
n = 0 is taken from the middle, n = 1 is one either side and so on
Young's Double Slit Experiment
Young’s double-slit experiment demonstrates how light waves can produce an interference pattern
The setup of the experiment is shown below:
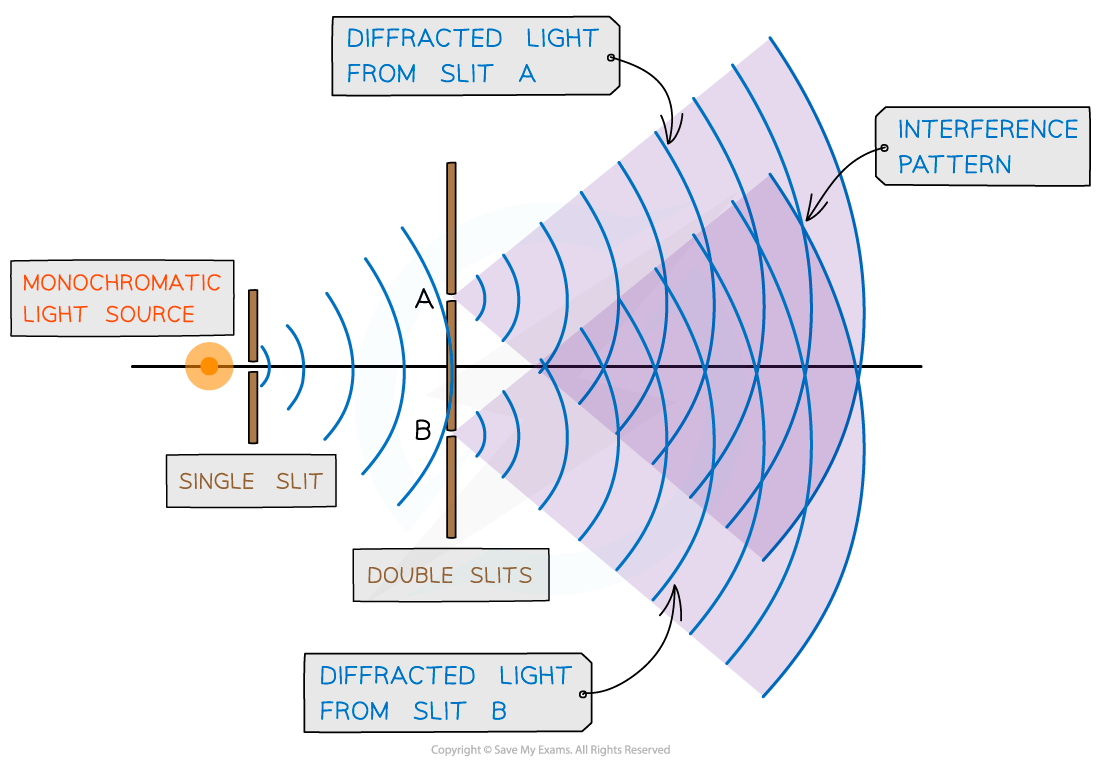
Young’s double-slit experiment arrangement
When a monochromatic light source is placed behind a single slit, the light is diffracted producing two light sources at the double slits A and B
Since both light sources originate from the same primary source, they are coherent and will therefore create an observable interference pattern
Both diffracted light from the double slits create an interference pattern made up of bright and dark fringes
Wave Nature of Light
Interference is a confirmation of the wave-nature of light
Newton initially proposed that visible light is a stream of microscopic particles called corpuscles
However, these corpuscles could not explain interference or diffraction effects, therefore, the view of light as a wave was adopted instead
Not long after, Huygens came up with the original Wave Theory of Light to explain the phenomena of diffraction and refraction
This theory describes light as a series of wavefronts on which every point is a source of waves that spread out and travel at the same speed as the source wave
These are known as Huygens’ wavelets
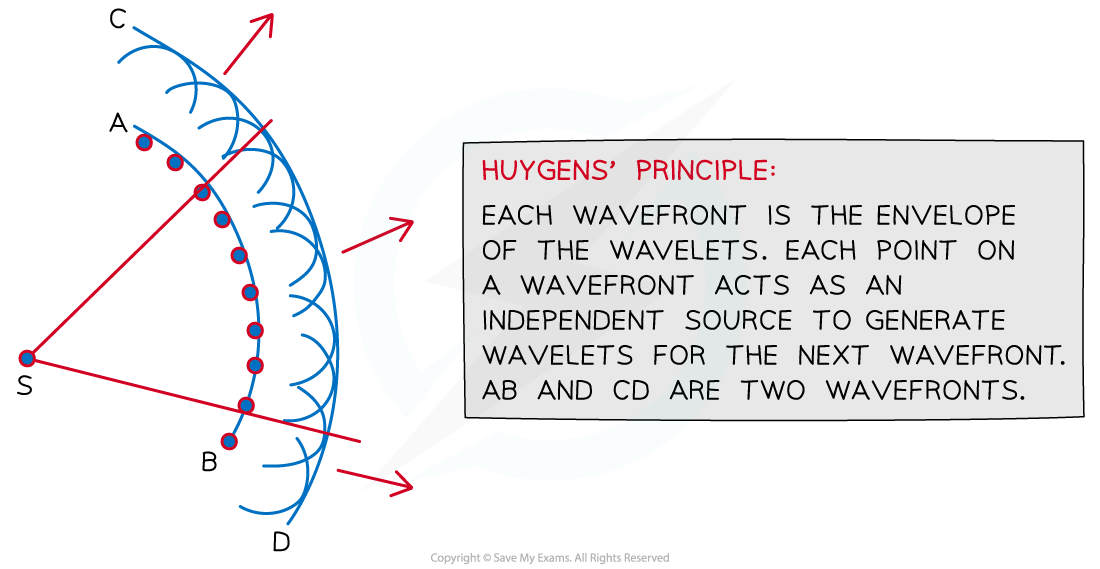
Huygen's wavelets shown by two wavefronts AB and CD
Examiner Tips and Tricks
The path difference is more specifically how much longer, or shorter, one path is than the other. In other words, the difference in the distances. Make sure not to confuse this with the distance between where the two paths begin
Double-Slit Equation
The fringe width, wavelength of the light, distance between the slits or the distance from the slits to the screen can be calculated using the double-slit equation:
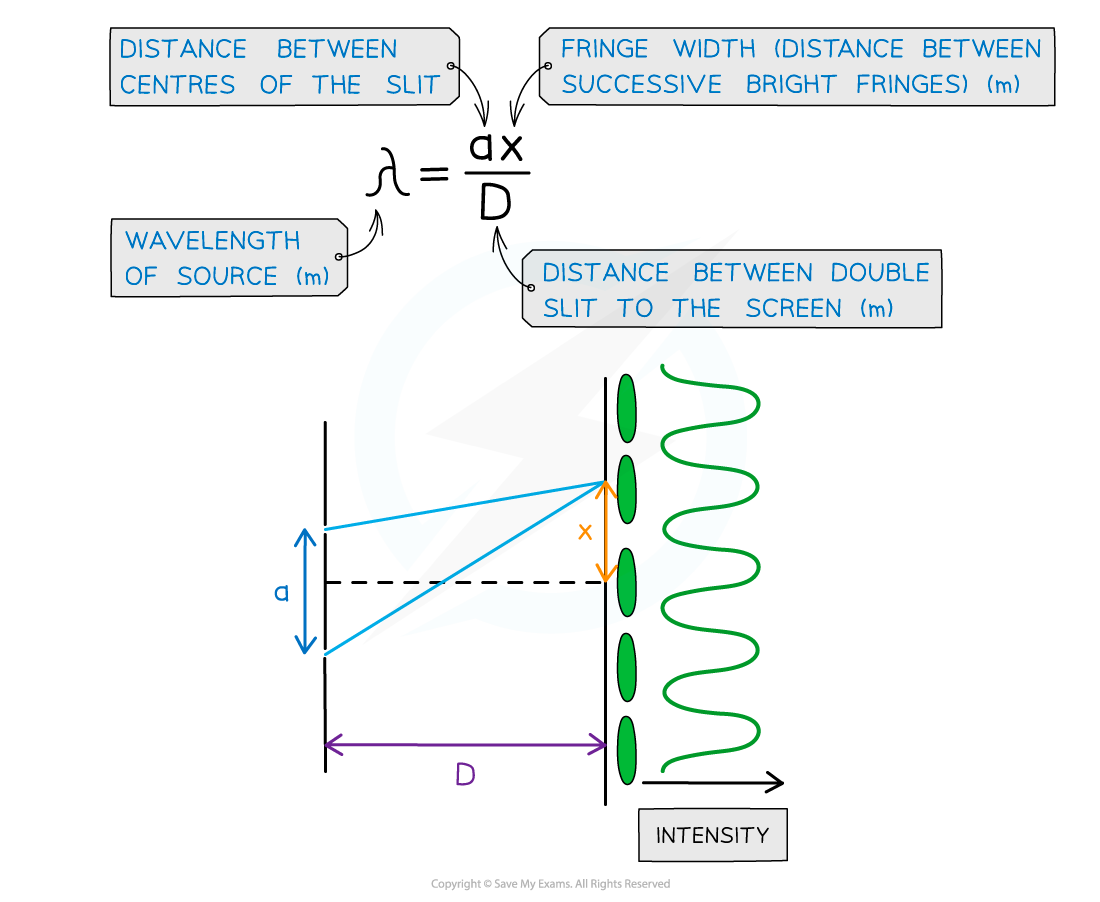
Double slit interference equation with a, x and D represented on a diagram
This equation is only when a << D
The interference pattern on a screen will show as ‘fringes’ which are dark or bright bands
Constructive interference is shown through bright fringes with varying intensity (most intense in the middle)
Destructive interference is shown from dark fringes where no light is seen
A monochromatic light source makes these fringes clearer and the distance between fringes is very small due to the short wavelength of visible light
Worked Example
A laser is placed in front of a double-slit as shown in the diagram below.
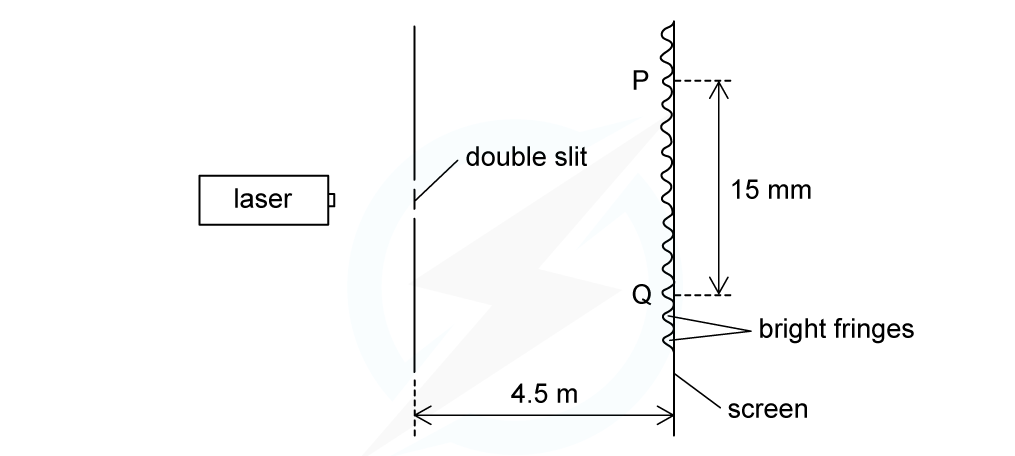
The laser emits light of frequency 750 THz. The separation of the maxima P and Q observed on the screen is 15 mm. The distance between the double slit and the screen is 4.5 m. Calculate the separation of the two slits.
Answer:

Examiner Tips and Tricks
Since a, x and D are all distances, it's easy to mix up which they refer to. Labelling the double-slit diagram in the way given in the notes above will help to remember the order i.e. a and x in the numerator and D underneath in the denominator.

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
