Collisions (OCR A Level Physics) : Revision Note
Collisions in One & Two Dimensions
One-dimensional Problems
Momentum (p) is equal to: p = m × v
One-dimensional momentum problems are when collisions are taken place in just the x (horizontal) or just the y (vertical) direction
Using the conservation of linear momentum, it is possible to calculate missing velocities and masses of components in the system
This is shown in the example below:
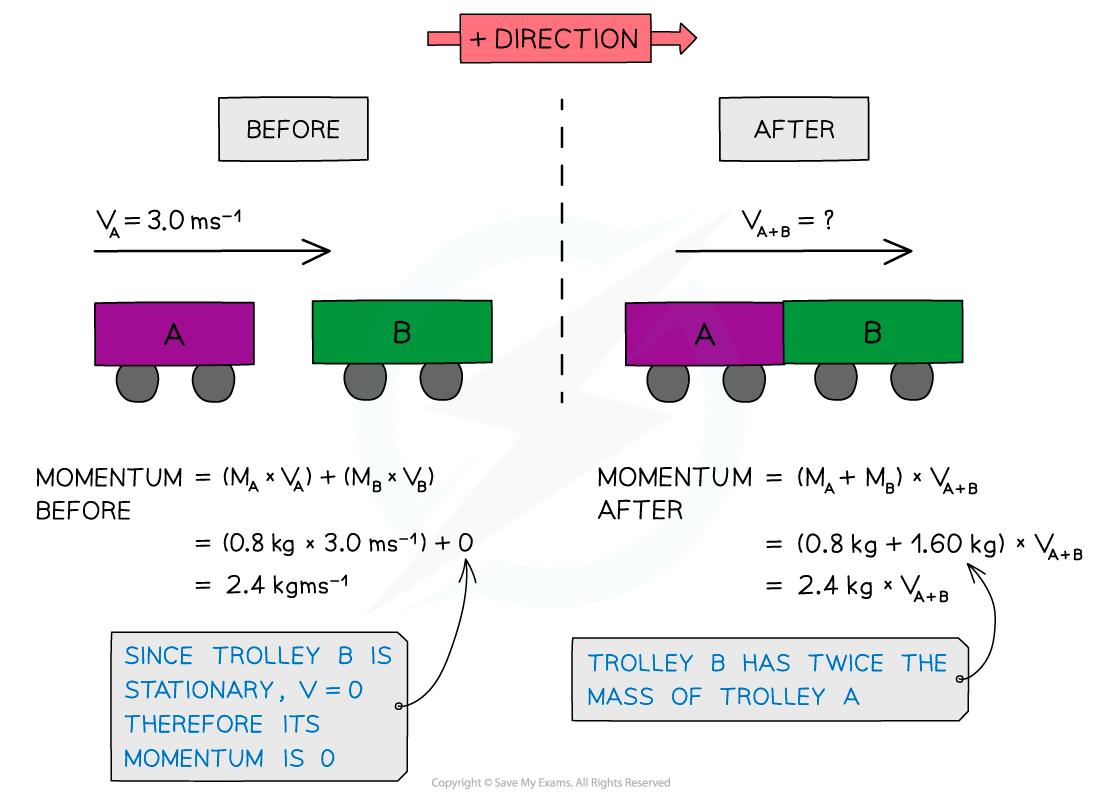
Worked Example
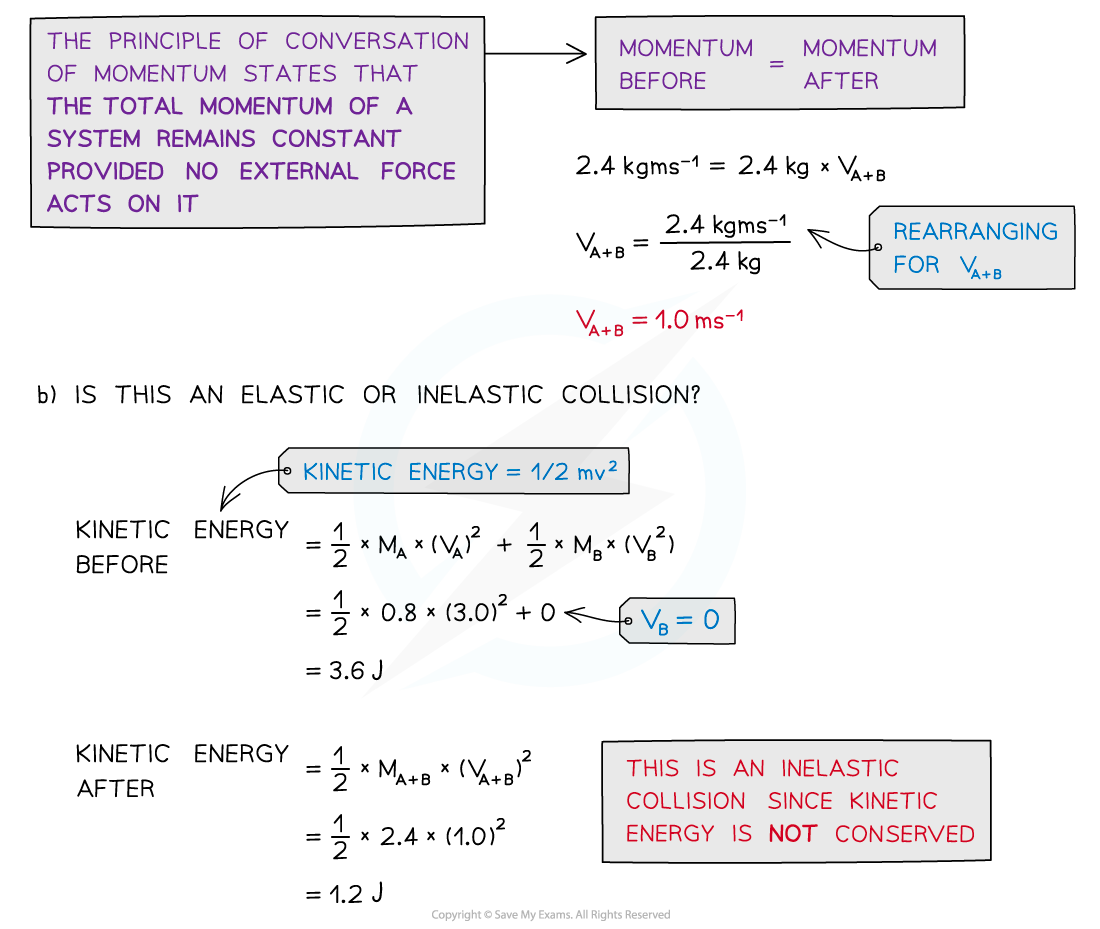
Trolley A of mass 0.80 kg collides head-on with stationary trolley B at a velocity of 3.0 ms-1.Trolley B has twice the mass of trolley A. The trolleys stick together. Using the conservation of momentum, calculate the common velocity of both trolleys after the collision. Determine whether this is an elastic or inelastic collision.
Answer:
Two-dimensional Momentum Problems
Since momentum is a vector, in 2D it can be split up into its x and y components
Two-dimensional momentum problems are when collisions are taken place in both the x (horizontal) and the y (vertical) direction
Using the conversation of linear momentum as well as resolving vectors, it is possible to calculate changes in momentum
This is shown in the example below:
Worked Example
A ball is thrown at a vertical wall. The path of the ball is shown below
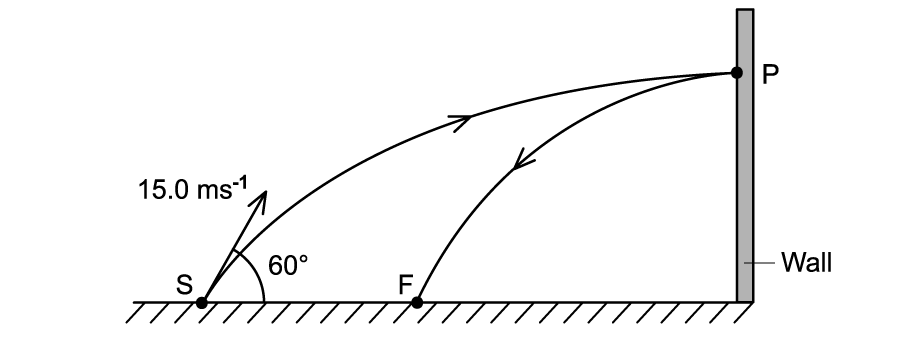
The ball is thrown from S with an initial velocity of 15.0 m s-1 at 60.0° to the horizontal. The mass of the ball is 60 × 10-3 kg and rebounds at a velocity of 4.6 m s-1.Calculate the change in momentum of the ball if it rebounds off the wall at P.
Answer:

Examiner Tips and Tricks
If an object is stationary or at rest, it’s velocity equals 0, therefore, the momentum and kinetic energy are also equal to 0.When a collision occurs in which two objects are stuck together, treat the final object as a single object with a mass equal to the sum of the two individual objects. In 2D problems, make sure you’re confident resolving vectors. Here is a small trick to remember which component is cosine or sine of the angle for a vector R:

Resolving vectors with sine and cosine
Elastic & Inelastic Collisions
In both collisions and explosions, momentum is always conserved
However, kinetic energy might not always be
A collision (or explosion) is either:
Elastic – if the kinetic energy is conserved
Inelastic – if the kinetic energy is not conserved
Collisions are when objects striking against each other
Elastic collisions are commonly those where objects colliding do not stick together and then move in opposite directions
Inelastic collision are commonly those where objects collide and stick together after the collision
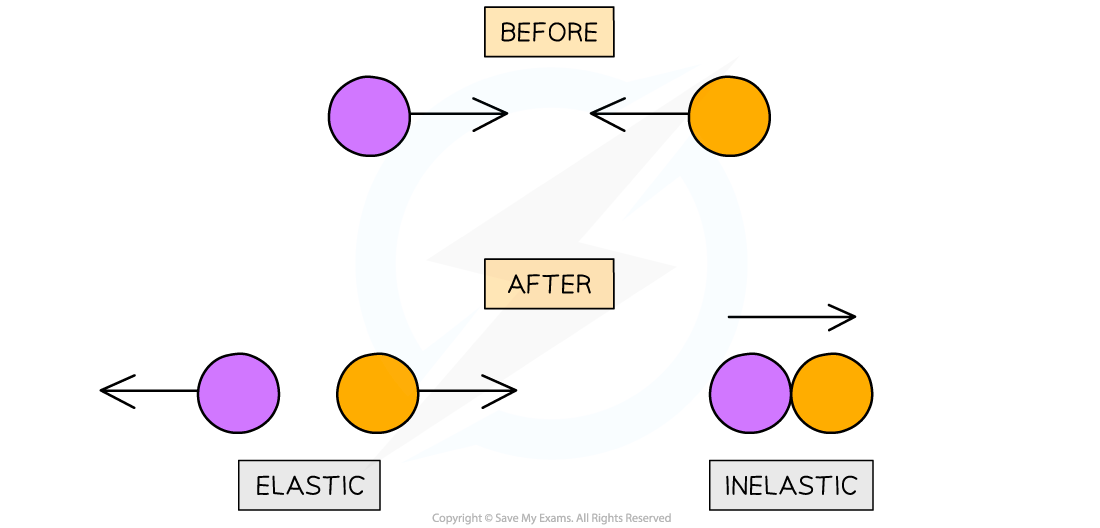
Elastic collisions are where two objects move in opposite directions. Inelastic collisions are where two objects stick together
An explosion is commonly to do with recoil
For example, a gun recoiling after shooting a bullet or an unstable nucleus emitting an alpha particle and a daughter nucleus
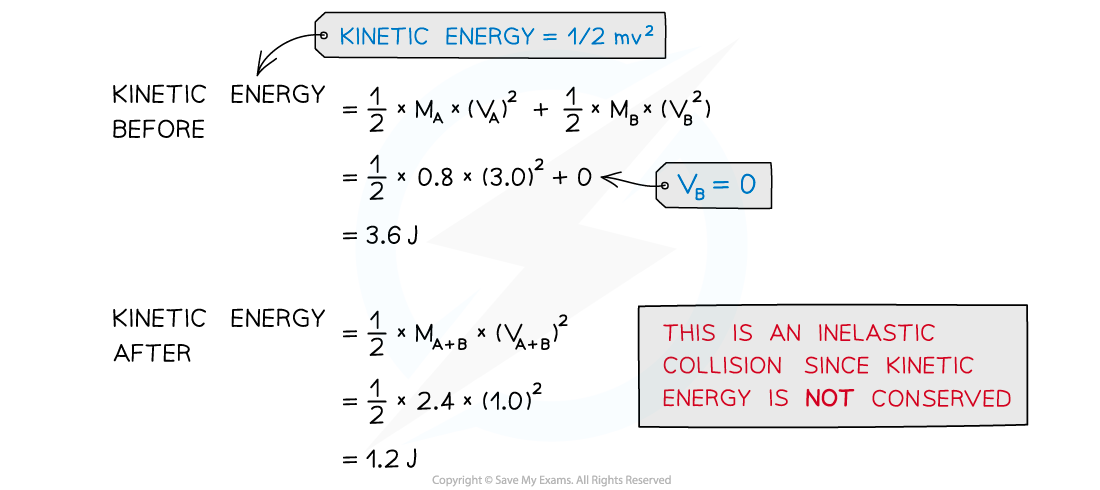
To find out whether a collision is elastic or inelastic, compare the kinetic energy before and after the collision
The equation for kinetic energy is:

Worked Example
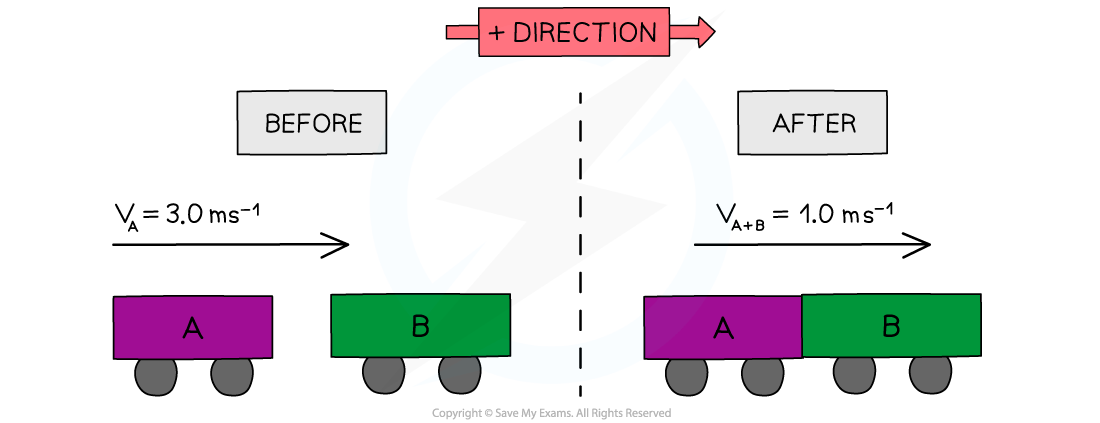
Trolley A of mass 0.80 kg collides head-on with stationary trolley B at speed 3.0 m s–1. Trolley B has twice the mass of trolley A. The trolleys stick together and travel at a velocity of 1.0 m s–1.Determine whether this is an elastic or inelastic collision.
Answer:
Examiner Tips and Tricks
If an object is stationary or at rest, it’s velocity equals 0, therefore, the momentum and kinetic energy are also equal to 0.When a collision occurs in which two objects are stuck together, treat the final object as a single object with a mass equal to the sum of the two individual objects.

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
