Impulse on a Force-Time Graph (OCR A Level Physics)

• In real life, forces are often not constant and will vary over time
• If the force is plotted against time, the impulse is equal to the area under the force-time graph

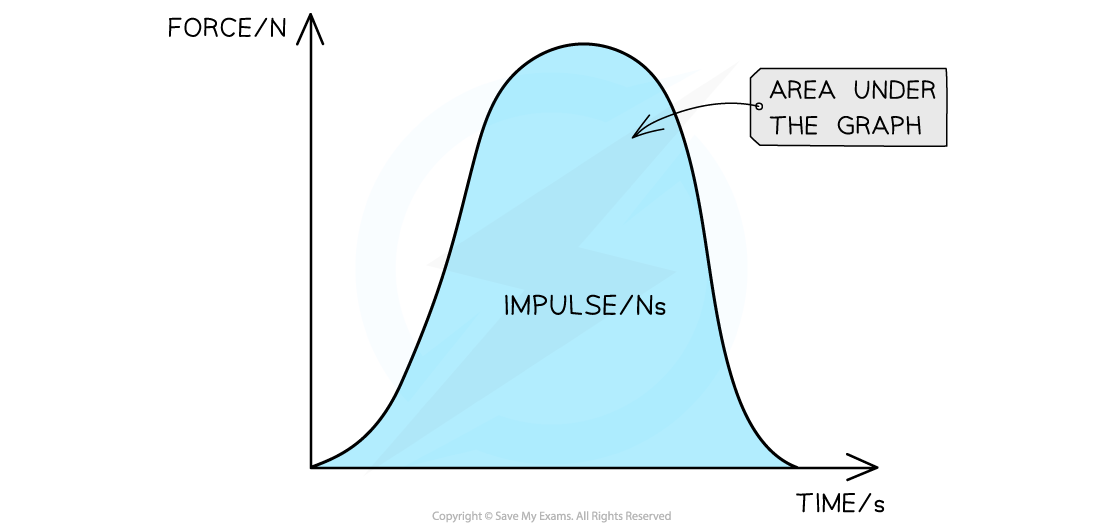
When the force is not constant, the impulse is the area under a force–time graph

• This is because

Impulse = FΔt

• Where:
  • F = force (N)
  • Δt = change in time (s)

• The impulse is therefore equal whether there is
  • A small force over a long period of time
  • A large force over a small period of time

• The force-time graph may be a curve or a straight line
  • If the graph is a curve, the area can be found by counting the squares underneath
  • If the graph is made up of straight lines, split the graph into sections. The total area is the sum of the areas of each section

Step 1: List the known quantities

• • Mass, m = 3.0 kg
  • Initial velocity, u = 0 m s^-1 (since it is initially at rest)

Step 2: Calculate the impulse

• • The impulse is the area under the graph
  • The graph can be split up into two right-angled triangles with a base of 8 s and a height of 4 kN

Area = Impulse = 32 × 10³ N s

Step 3: Write the equation for impulse

Impulse, I = Δp = m(v – u)

Step 4: Substitute in the values

I = mv

32 × 10³ = 3.0 × v

v = (32 × 10³) ÷ 3.0

v = 10666 m s^–1 = 11 km s^-1