Elastic Potential Energy (OCR A Level Physics) : Revision Note
Area under a Force-Extension Graph
Work has to be done to stretch a material
Before a material reaches its elastic limit (whilst it obeys Hooke's Law), all the work done is stored as elastic strain energy
The work done, or the elastic strain energy is the area under the force-extension graph
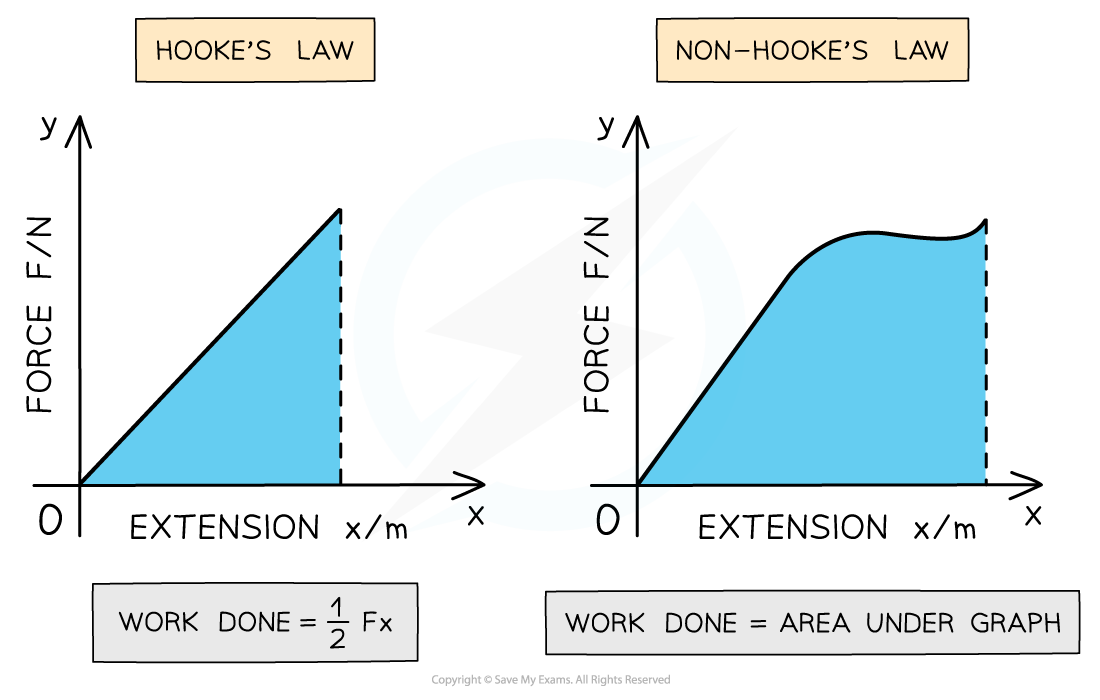
Work done is the area under the force-extension graph
This is true for whether the material obeys Hooke’s law or not
For the region where the material obeys Hooke’s law, the work done is the area of a right-angled triangle under the graph
For the region where the material doesn’t obey Hooke’s law, the area is the full region under the graph. To calculate this area, split the graph into separate segments and add up the individual areas of each
Worked Example
The graph shows the behaviour of a sample of a metal when it is stretched until it starts to undergo plastic deformation.

What is the total work done in stretching the sample from zero to 13.5 mm extension?
Simplify the calculation by treating the curve XY as a straight line.
Answer:
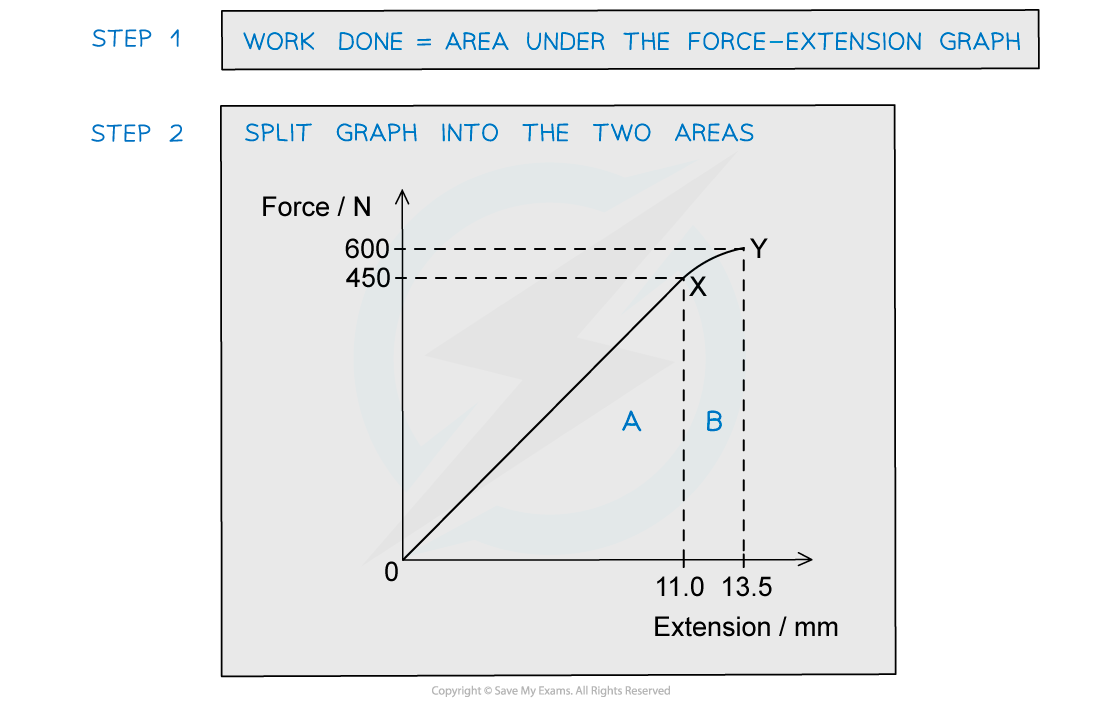

Worked Example
A spring is extended with varying forces; the graph below shows the results.

What is the energy stored in the spring when the extension is 40 mm?
Answer:
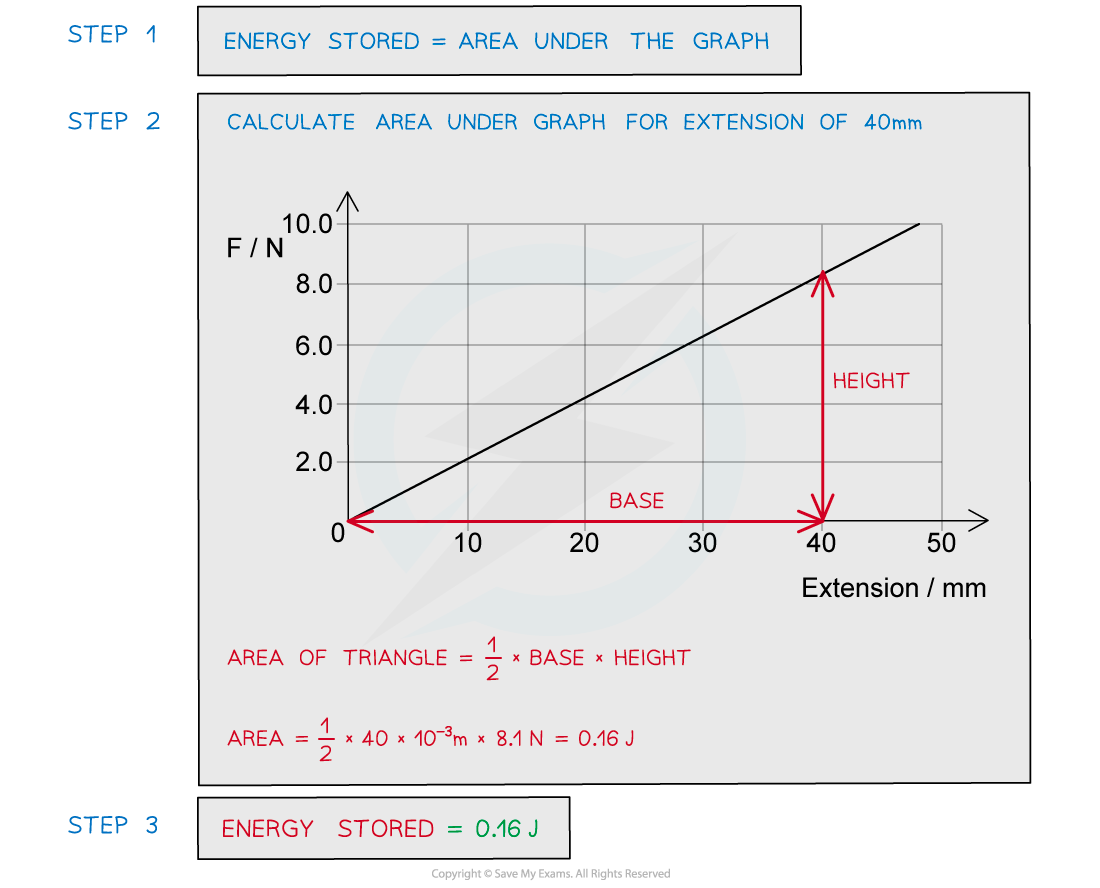
Examiner Tips and Tricks
Remember to always double-check the units on the force and extension axes on the graph before using values from it for calculations. The force can sometimes be in kN and the extension in mm!
Elastic Potential Energy
Elastic potential energy is defined as
The energy stored within a material (e.g. in a spring) when it is stretched or compressed
It can be found from the area under the force-extension graph for a material deformed within its limit of proportionality
A material within its limit of proportionality obeys Hooke’s law
Therefore, for a material obeying Hooke’s Law, elastic potential energy can be calculated using:

Where:
k = force constant of the spring (N m-1)
x = extension (m)
It is very dangerous if a wire under stress suddenly breaks
This is because the elastic potential energy of the strained wire is converted into kinetic energy
EPE = KE
½ kx2 = ½ mv2
v ∝ x
This equation shows that the greater the extension of a wire, x, the greater the speed, v, it will have on breaking
Worked Example
A car’s shock absorbers make a ride more comfortable by using a spring that absorbs energy when the car goes over a bump. One of these springs, with a force constant of 50 kN m-1 is fixed next to a wheel and compressed a distance of 10 cm. Calculate the energy stored by the compressed spring.
Answer:
Step 1: List the known values
Force constant, k = 50 kN m-1 = 50 × 103 N m-1
Compression, x = 10 cm = 10 × 10-2 m
Step 2: Write the relevant equation
EPE = ½ kx2
Step 3: Substitute in the values
EPE = ½ × (50 × 103) × (10 × 10-2)2 = 250 J

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
