Force-Extension Graphs (OCR A Level Physics)

Force-Extension Graphs

• The way a material responds to a given force can be shown on a force-extension graph

• Every material will have a unique force-extension graph depending on how brittle or ductile it is

• A material may obey Hooke's Law up to a point

  • This is shown on its force-extension graph by a straight line through the origin

• As more force is added, the graph may start to curve slightly

The Hooke's Law region of a force-extension graph is a straight line. The spring constant is the gradient of that region

The key features of the graph are:

• The limit of proportionality

  • The point beyond which Hooke's law is no longer true when stretching a material i.e. the extension is no longer proportional to the applied force

  • The point is identified on the graph where the line starts to curve (flattens out)

• The force constant k is the force per unit extension up to the limit of proportionality, after which the material will not obey Hooke’s law

  • This is the gradient of the straight part of the graph

• The graph might also include the elastic limit, this is:

  • The maximum amount a material can be stretched and still return to its original length (above which the material will no longer be elastic)

  • This point is always after the limit of proportionality

• Therefore, k is the gradient of the linear part of the graph ie. where Hooke's Law is obeyed

Metal Wire

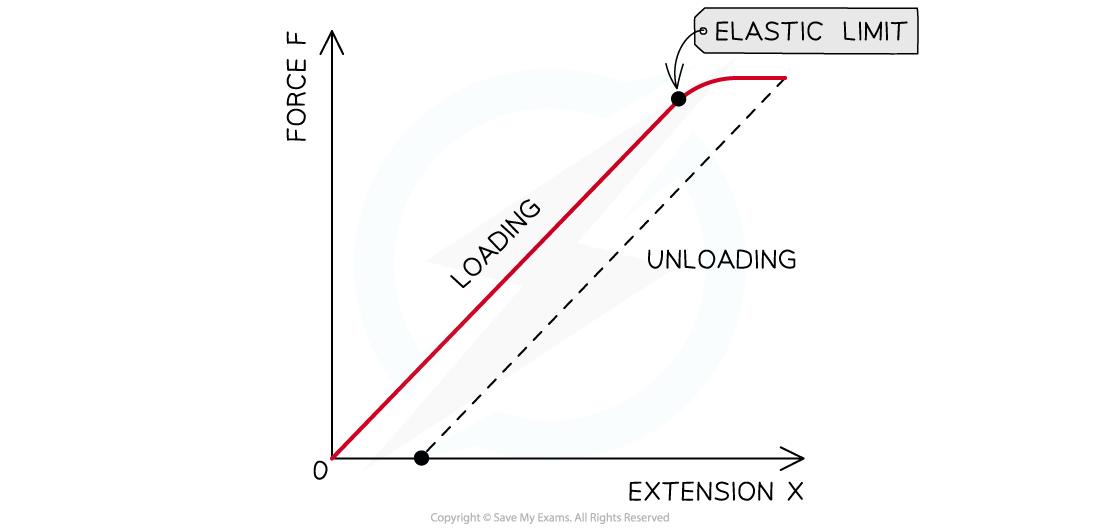
• A metal wire obeys Hooke’s law and exhibits elastic deformation until its elastic limit

  • Up to this point, the loading curve is the same as the unloading curve

• Beyond this point, it experiences plastic deformation

  • The unloading curve has the same gradient as the loading curve

  • The plastic deformation causes a permanent extension of the wire

Rubber

• Rubber is an elastic material, so it does not experience plastic deformation, nor does it obey Hooke’s law

• The area between the loading and unloading curves is known as a hysteresis loop

  • This area represents the work done in stretching the material

  • This energy is transferred to thermal energy when the force is removed

• An example of a force-extension graph for such a material is:

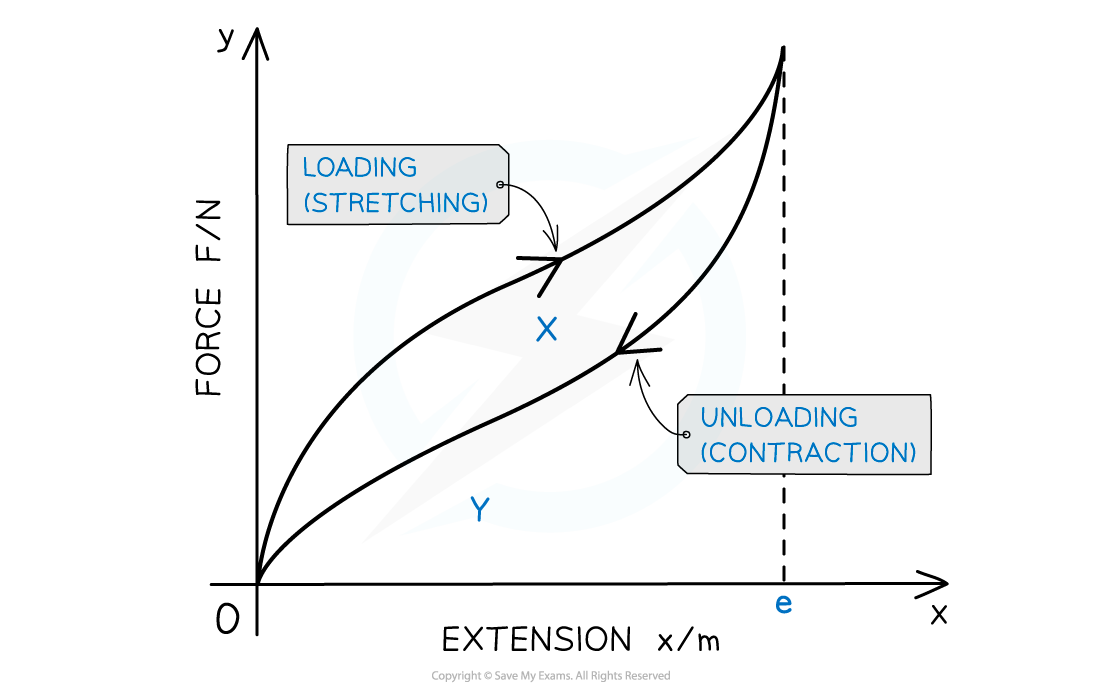
• The curve for contraction is always below the curve for stretching

• The area X represents the net work done or the thermal energy dissipated in the material

• The area X + Y is the minimum energy required to stretch the material to extension e

Polymeric Materials (Polyethene)

• Polyethene is a common polymer or polymeric material

• It does not obey Hooke’s law and experiences plastic deformation when any force is applied to it

• This makes it very easy to stretch into new shapes, but difficult to return to its original shape

Investigating Force-Extension Characteristics

Aims of the Experiment

The aim of this experiment is to investigate the relationship between force and extension for three materials: metal springs, rubber bands and polythene strips

Variables

• Independent variable = Force / Load (N)

• Dependent variable = Extension (m)

Equipment List

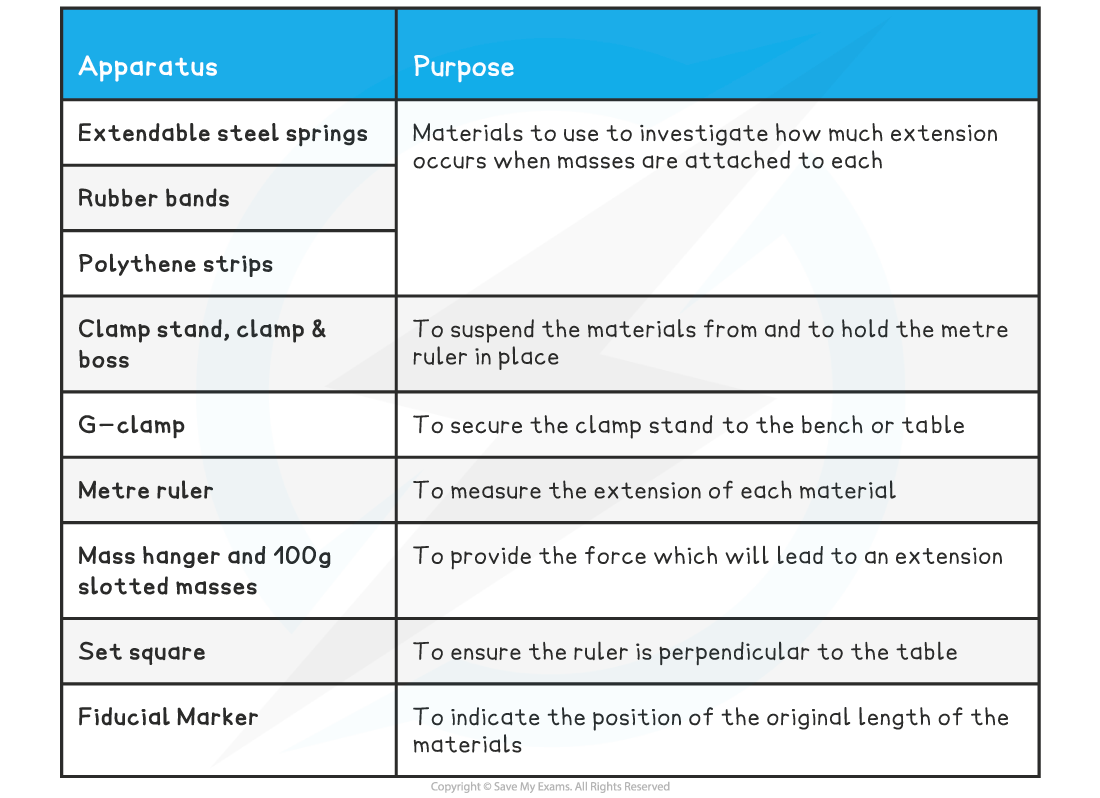
• Resolution of measuring equipment:

  • Metre ruler = 1 mm

Method

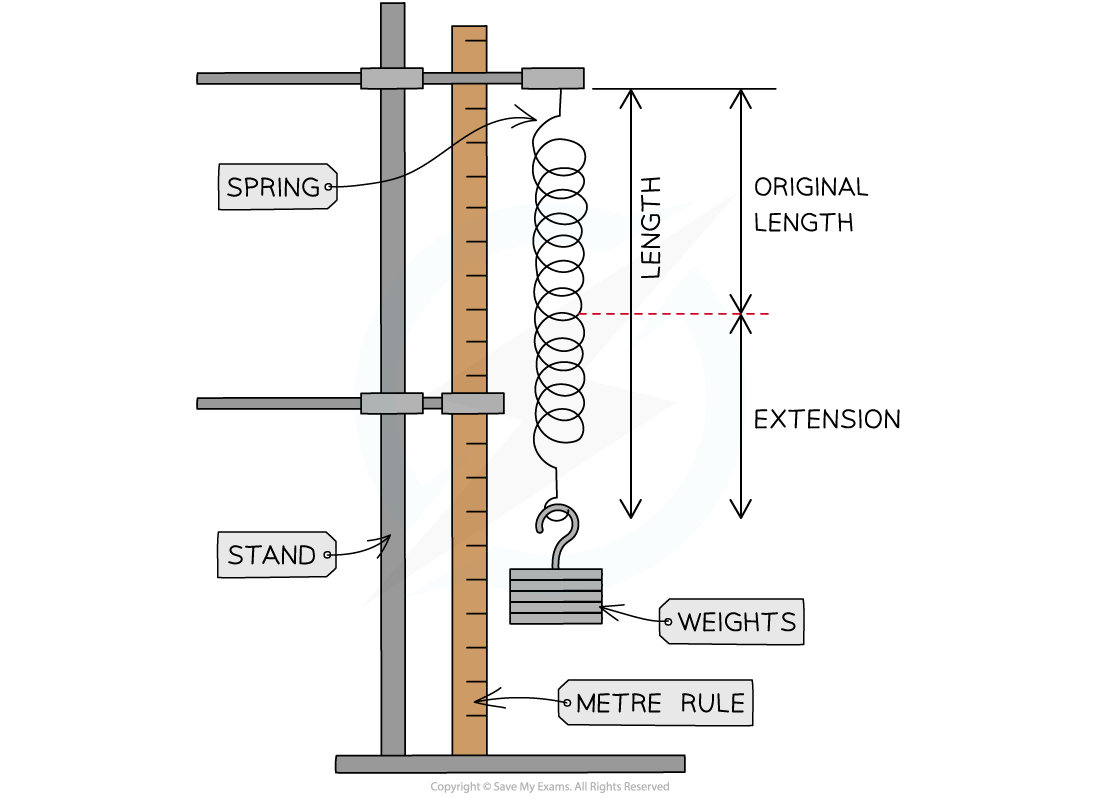
Experimental set-up for investigating force-extension characteristics of a metal spring

1. Set up the apparatus as shown in the diagram. Hang a spring from the clamp and boss and secure it so that it will not fall off

2. Secure the metre rule vertically to the clamp, using the set square to ensure it is straight and place it adjacent to the spring

3. Record the metre rule reading at the bottom of the spring and place a fiducial marker on this point. This is its original length before any masses are hanging from it (no load)

4. Hang a mass hanger from the bottom of the spring. Record the new metre rule reading, the number of masses and the extension of the spring

5. Add another mass. Record the new metre rule reading, the number of masses, and the total extension of the spring from its original length

6. Repeat this until after the spring has become permanently stretched

7. Repeat the experiment for the rubber band and the polythene strip

• An example table might look like this:

Analysing the Results

• According to Hooke’s Law:

F = kx

• Comparing this to the equation of a straight-line, y = mx

  • y = Load / force, F

  • x = Extension, x

  • Gradient = Force constant, k

• Plot a graph of the load applied on the horizontal axis and the extension of the spring on the vertical axis and draw a line of best fit

• The gradient of the linear part will be equal to the force constant, k

  • Make sure to measure the gradient of the straight section of the line only, as this is within the elastic limit of the material

Evaluating the Experiment

Systematic errors:

• Reduce parallax error by reading the metre ruler at eye-level

• Use a set square to make sure the ruler is straight and perpendicular to the bench or table

• Use a fiducial marker to mark the original position of the material

Random errors:

• Ensure the material is stationary before a reading is made

• Repeat the experiment several times and calculate an average

Safety Precautions

• When stretching materials, there is a danger that they may snap under the high tension

  • Eye protection should be worn

  • A box or landing mat should be placed below the hanger to catch the weight if it falls

  • Make sure to not stand directly underneath the hanging masses