Gravitational Potential Energy (OCR A Level Physics) : Revision Note
Gravitational Potential Energy (Eₚ)
Gravitational potential energy (Ep) is energy stored in a mass due to its position in a gravitational field
If a mass is lifted up, it will gain Ep (converted from other forms of energy)
If a mass falls, it will lose Ep (and be converted to other forms of energy)
The equation for gravitational potential energy for energy changes in a uniform gravitational field is:


Gravitational potential energy (GPE): The energy an object has when lifted up
The potential energy on the Earth’s surface at ground level is taken to be equal to 0
This equation is only relevant for energy changes in a uniform gravitational field (such as near the Earth’s surface)
Derivation of GPE Equation
When a heavy object is lifted, work is done since the object is provided with an upward force against the downward force of gravity
Therefore energy is transferred to the object
This equation can therefore be derived from the work done

Worked Example
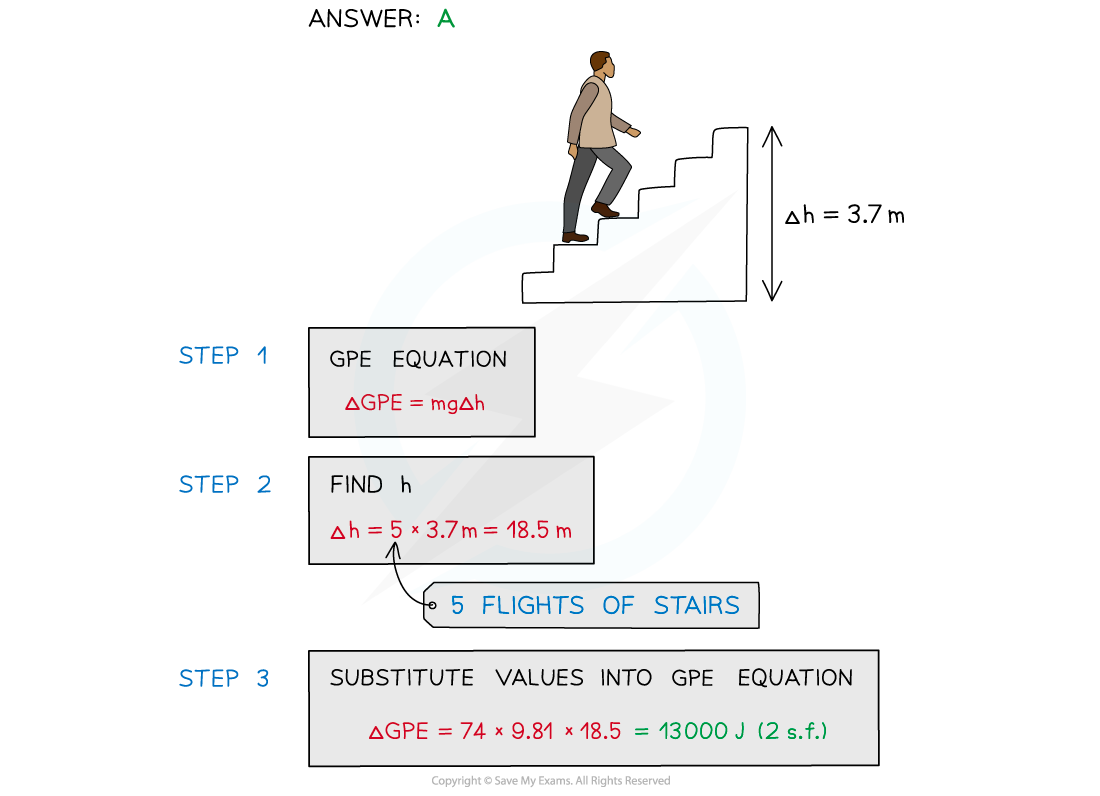
To get to his apartment a man has to climb five flights of stairs.
The height of each flight is 3.7 m and the man has a mass of 74 kg.
What is the approximate gain in the man's gravitational potential energy during the climb?
A. 13 000 J
B. 2700 J
C. 1500 J
D. 12 500 J
Examiner Tips and Tricks
In your exam, you will be expected to know how to derive the gravitational potential energy equation from first principles, so make sure to practice this derivation!
Exchange Between Eₖ and Eₚ
There are many scenarios that involve the transfer of kinetic energy into gravitational potential, or vice versa
Some examples are:
A swinging pendulum
Objects in freefall
Sports which involve falling, such as skiing and skydiving
Using the principle of conservation of energy, and taking any drag forces as negligible:
Loss in potential energy = Gain in kinetic energy
Worked Example
The diagram below shows a skier on a slope descending 750 m at an angle of 25° to the horizontal.
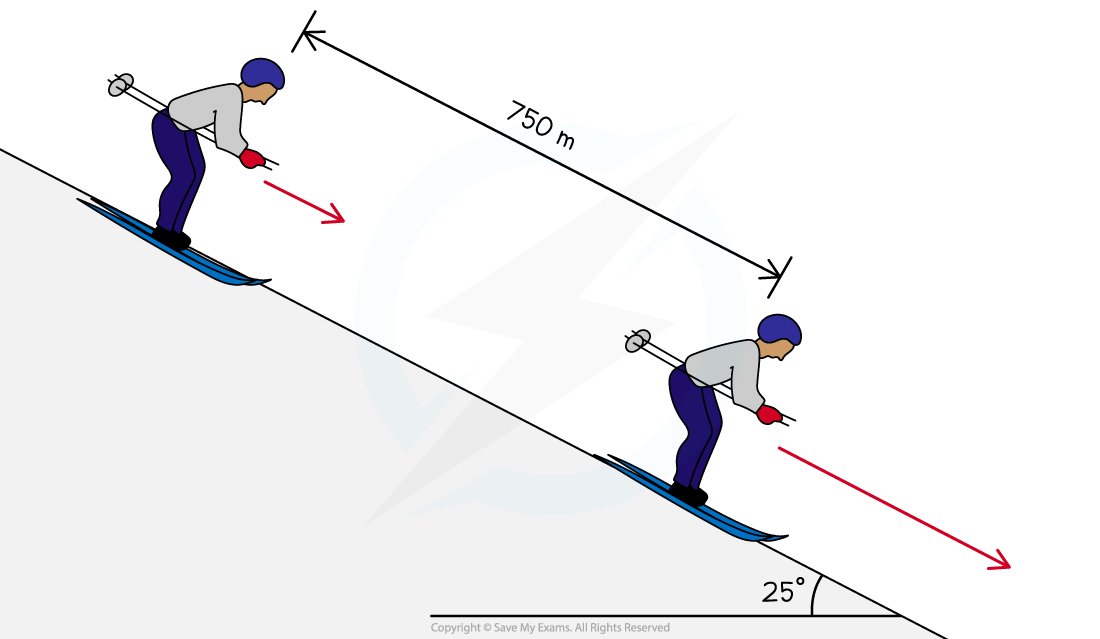
Calculate the final speed of the skier, assuming that he starts from rest and 15% of his initial gravitational potential energy is not transferred to kinetic energy.
Answer:
Step 1: Write down the known quantities
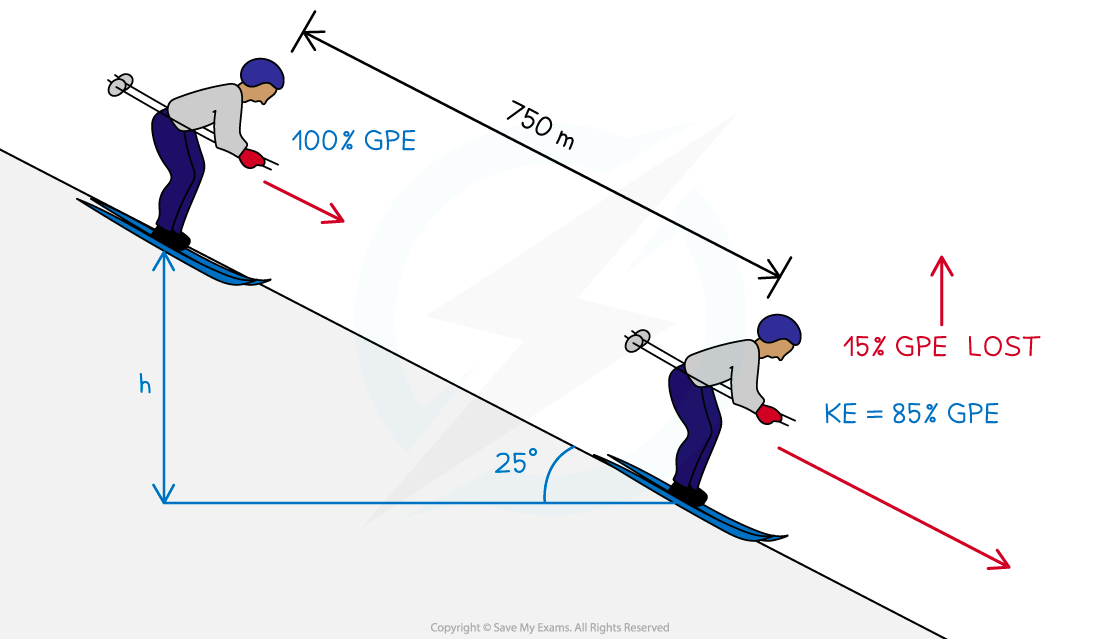
Vertical height, h = 750 sin 25°
Ek = 0.85 Ep
Step 2: Equate the equations for Ek and Ep
Ek = 0.85 Ep
½ mv2 = 0.85 × mgh
Step 3: Rearrange for final speed, v
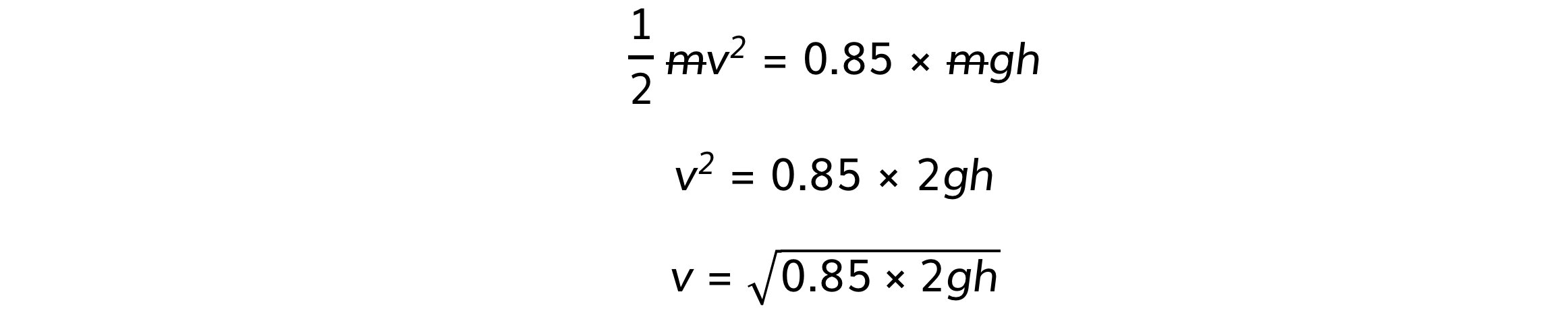
Step 4: Calculate the final speed, v

Examiner Tips and Tricks
GPE:
This equation only works for objects close to the Earth’s surface where we can consider the gravitational field to be uniform.
At A level, you might have to consider examples where the gravitational field is not uniform, such as in space, where this equation for GPE will not be relevant.
KE:
When using the kinetic energy equation, note that only the speed is squared, not the mass or the ½.
If a question asks about the ‘loss of kinetic energy’, remember not to include a negative sign since energy is a scalar quantity.

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
