Tension, Normal force, Upthrust & Friction (OCR A Level Physics)

• Tension:

The force experienced by a cable, rope, or string when pulled, hung, rotated or supported

• This is normally labelled as T on free body diagrams

Tension always acts away from the mass

• Normal Contact Force:

The force arising when an object rests against another object acting at a 90° angle to the plane of contact

• It is sometimes also referred to as the reaction force
• This is normally labelled as N or R on free body diagrams
• This force arises from Newton's Third Law

Normal contact force always acts perpendicular to the surface

• Upthrust:

The upward buoyancy force acting on an object when it is in a fluid

• Upthrust can occur in liquids and gases

Upthrust always acts upwards

• Friction:

The force that arises when two surfaces are in contact with each other

• Friction always opposes the motion
• This is normally labelled as F or Fr on free body diagrams

Friction always acts at the point where the objects are in contact, and in the opposite direction to the direction of motion

• Free body diagrams are useful for modelling the forces that are acting on an object
• Each force is represented as a vector arrow, where each arrow:
  • Is scaled to the magnitude of the force it represents
  • Points in the direction that the force acts
  • Is labelled with the name of the force it represents

• Free body diagrams can be used:
  • To identify which forces act in which plane
  • To resolve the net force in a particular direction

• The net force in a particular direction can be calculated by:
  • Using the labelled angles and magnitudes
  • Resolving each force into horizontal and vertical components

Part (a)

• • The size of the arrows should be such that the 3 forces would make a closed triangle as they are in equilibrium

Part (b)

• • In problems such as this, it is best to resolve the forces parallel and perpendicular to the slope
  • Usually, an angle will be given to allow calculation of the weight in these directions

Part (c)

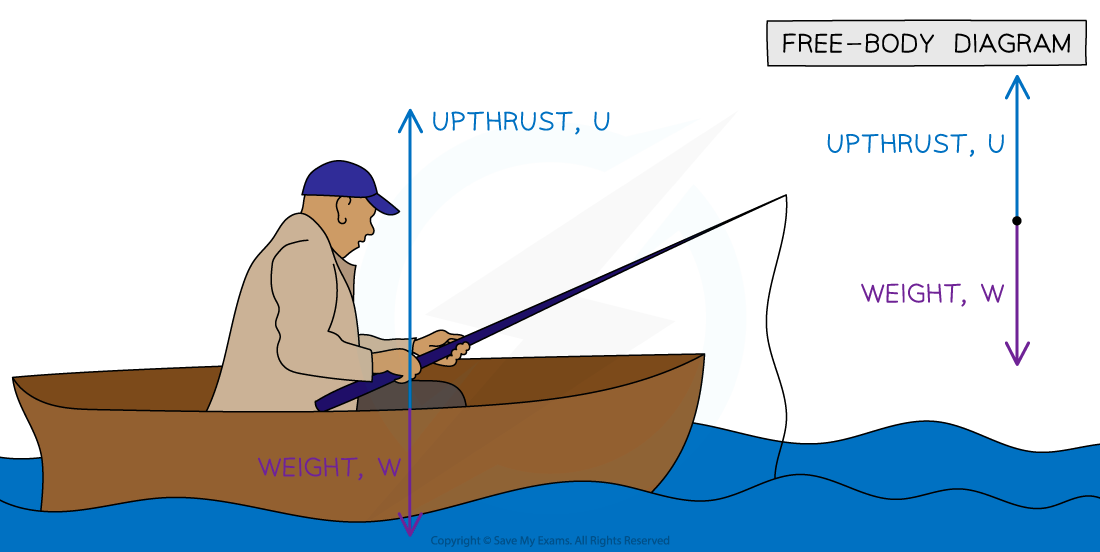
• • As the boat is not moving, the size of both arrows must be the same

Part (d)

• • As the car is accelerating, the size of the thrust must be larger than the size of the friction force
  • As in part (c), the upwards and downwards forces must be equal