SUVAT Equations (OCR A Level Physics) : Revision Note
SUVAT Equations
The SUVAT equations are the equations of motion used for objects in constant acceleration
They contain the following variables:
s = displacement (m)
u = initial velocity (m s-1)
v = final velocity (m s-1)
a = acceleration (m s-2)
t = time (s)
The 4 SUVAT equations are:

These are all given on the data sheet
All the variables, apart from time t, are vector quantities
This means they can either be positive or negative depending on their direction
The key terms to look out for are:
'Starts from rest', or if the initial velocity is not mentioned, this means u = 0
'Starts from rest' means an object starts from rest at x = 0 when t = 0
If an object is only 'falling due to gravity' then a = g = 9.81 m s-2
It doesn't matter which way is positive or negative for the scenario, as long as it is consistent for all the vector quantities
For example, if downwards is negative then for a ball travelling upwards, s must be positive and a must be negative
SUVAT equations are used for motion with constant acceleration in a straight line
For example, an object falling in a uniform gravitational field without air resistance
How to Use the SUVAT Equations
Step 1: Write out the variables that are given in the question, both known and unknown, and use the context of the question to deduce any quantities that aren’t explicitly given
e.g. for vertical motion a = ± 9.81 m s–2, an object which starts or finishes at rest will have u = 0 or v = 0
Step 2: Choose the equation which contains the quantities you have listed
e.g. the equation that links s, u, a and t is s = ut + ½at2
Step 3: Convert any units to SI units and then insert the quantities into the equation and rearrange algebraically to determine the answer
Sometimes the question may have to be split into two, where the SUVAT equations will have to be used twice
For example, if there are two masses connected over a pulley and one mass continues moving after the other has stopped
Worked Example
The diagram shows an arrangement to stop trains that are travelling too fast.
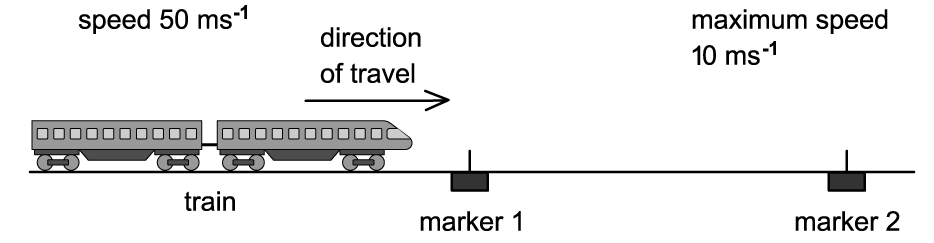
At marker 1, the driver must apply the brakes so that the train decelerates uniformly in order to pass marker 2 at no more than 10 m s–1.
The train carries a detector that notes the times when the train passes each marker and will apply an emergency brake if the time between passing marker 1 and marker 2 is less than 20 s.
Trains coming from the left travel at a speed of 50 m s–1.
Determine how far marker 1 should be placed from marker 2.
Answer:

Examiner Tips and Tricks
This is arguably the most important section of this topic, you can always be sure there will be one, or more, questions in the exam about solving problems with SUVAT equations
The best way to master this section is to practice as many questions as possible!

You've read 0 of your 5 free revision notes this week
Unlock more, it's free!
Did this page help you?
