Displacement, Velocity & Acceleration (OCR A Level Physics)

Scalar quantities

• Scalar quantities only have a magnitude (size)
  • Distance: the total length between two points
  • Speed: the total distance travelled per unit of time

Vector quantities

• Vector quantities have both magnitude and direction
  • Displacement: the distance of an object from a fixed point in a specified direction
  • Velocity: the rate of change of displacement of an object
  • Acceleration: the rate of change of velocity of an object

Equations for Velocity & Acceleration

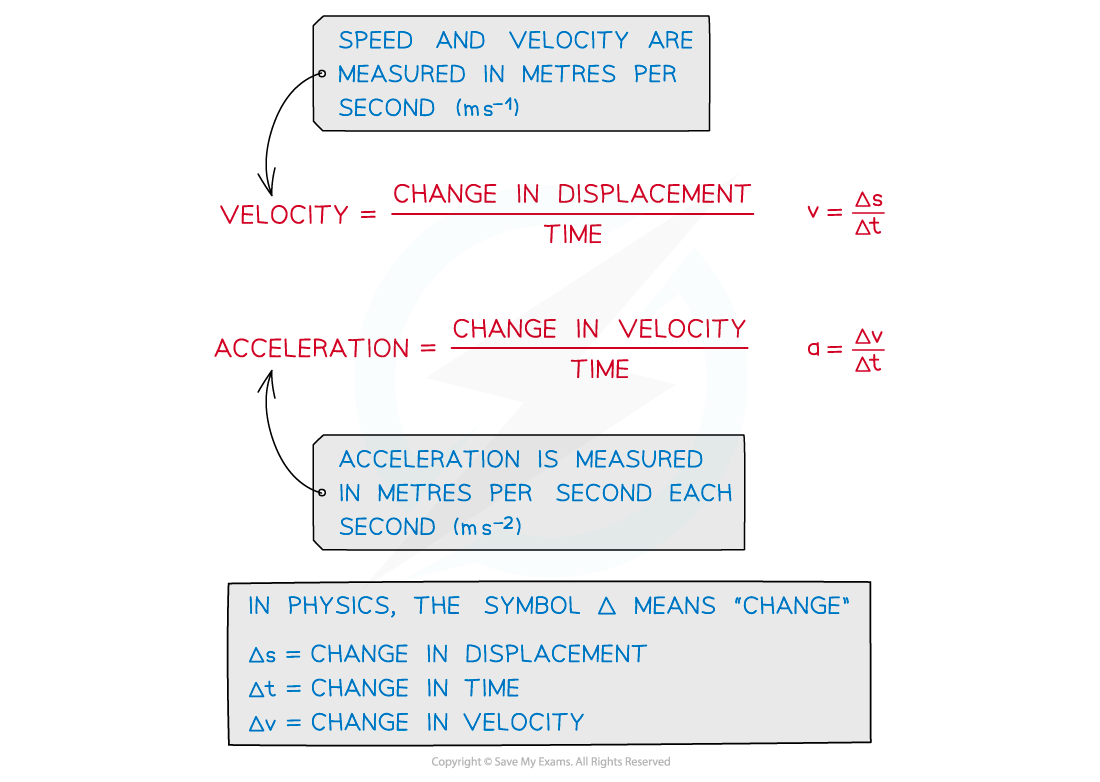
Equations linking displacement, velocity and acceleration

Instantaneous Speed / Velocity

• The instantaneous speed (or velocity) is the speed (or velocity) of an object at any given point in time
• This could be for an object moving at a constant velocity or accelerating
  • An object accelerating is shown by a curved line on a displacement – time graph
  • An accelerating object will have a changing velocity

• To find the instantaneous velocity on a displacement-time graph:
  • Draw a tangent at the required time
  • Calculate the gradient of that tangent

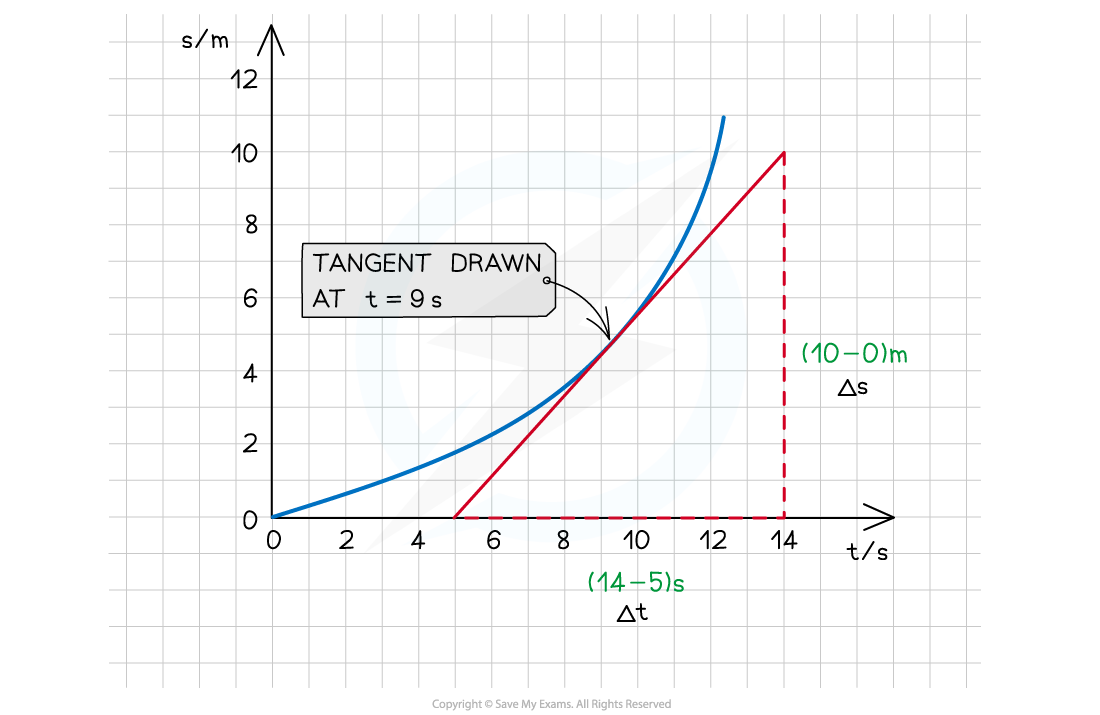
The instantaneous velocity is found by drawing a tangent on the displacement time graph

Average Speed / Velocity

• The average speed (or velocity) is the total distance (or displacement) divided by the total time
• To find the average velocity on a displacement-time graph, divide the total displacement (on the y-axis) by the total time (on the x-axis)
  • This method can be used for both a curved or a straight line on a displacement-time graph

Step 1: Write the average speed equation

Average speed = total distance ÷ total time

Step 2: Calculate the total distance

Total distance = 20 + 5 = 25 m

Step 3: Calculate the average speed

Average speed = 25 ÷ 3.5  = 7.1 m s^-1