Plotting & Interpreting Graphs (OCR A Level Physics): Revision Note
Exam code: H556
Plotting & Interpreting Graphs
When plotting graphs, it is important to consider the importance of the following factors:
Selecting appropriate scales
Labelling axes with quantities and units
Carefully plotting the points
Measurement of gradients and intercepts
Choice of Scale
When choosing a scale, it must be big enough to accommodate all the collected values using as much of the graph paper as possible
At least half of the graph grid should be occupied in both the x and y directions
Scales should be clearly indicated and have suitable, sensible ranges that are easy to work with
For example, scales with multiples of 3 should be avoided
The scales should increase outwards and upwards from the origin
Each axis should be labelled with the quantity that is being plotted, along with the correct unit
Labelling the Axes
Label each axis with the name of the quantity and its unit
For example, F / N means force measured in Newtons
The convention is that a forward slash ( / ) is used to separate the quantity and the unit
In general:
The independent variable goes on the x-axis
The dependent variable goes on the y-axis
Plotting the Points
Points should be plotted so that they all fit on the graph grid and not outside it
All values should be plotted, and the points must be precise to within half a small square
Points must be clear, and not obscured by the line of best fit, and they need to be plotted with a sharp pencil so that they are thin
There should be at least six points plotted on the graph, with any major outliers identified
Line or Curve of Best Fit
There should be equal numbers of points above and below the line of best fit
Using a clear plastic ruler will help with this
Not all lines will pass through the origin and nor should they be forced to
The line (or curve) of best fit should not be too thick or joined dot-to-dot like a frequency polygon
Anomalous values that have not been identified during the implementation stage should be ignored if they are obviously incorrect
This is because they will have a large effect on the gradient of the line of best fit
Calculating the Gradient
The gradient can be calculated by dividing the rise (change in y) by the run (change in x)
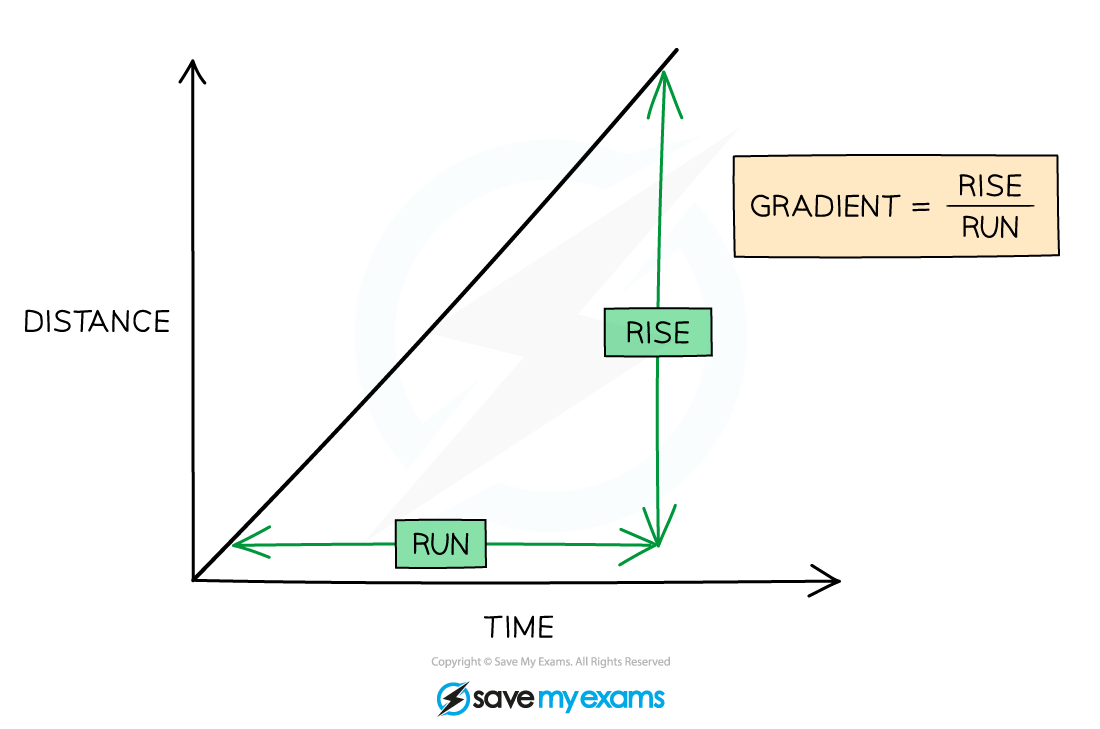
The calculation needs to be shown, including the correct substitution of identified plotted points from the axes into the equation
The triangle used to calculate the gradient should be drawn on the graph and it needs to be as large as possible
Small triangles are not acceptable for working out a gradient
When using the results from a table of values, the triangle that is used to obtain the gradient can utilise points that lie on the line of best fit but not values that lie away from the line
Determining the y-intercept
The y-intercept is the y value obtained where the line crosses the y-axis at x = 0
Values should be read accurately from the graph, with the scale on the y-axis being interpreted correctly
Worked Example
A student investigates the effect of placing an electric fan in front of a wind turbine. The wind turbine is connected to a voltmeter. When the wind turbine turns, it generates a voltage.The student obtains the following results:
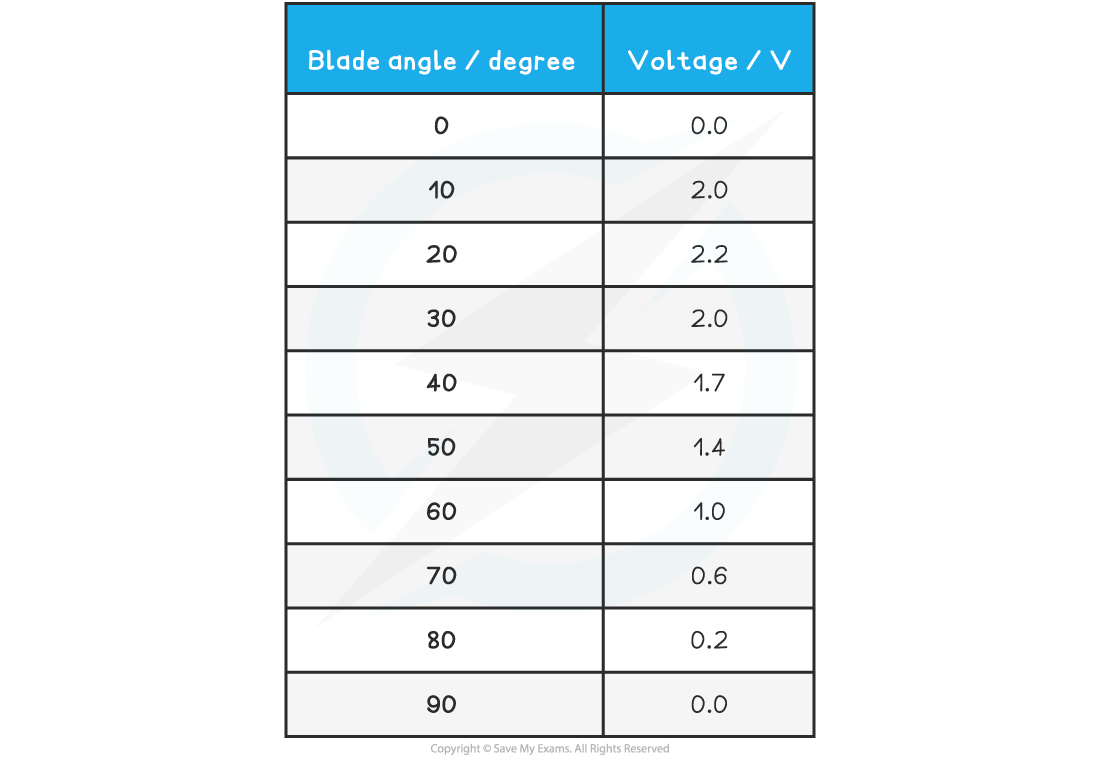
Plot the student’s results on the grid and draw a curve of best fit on the graph.

Answer:
Step 1: Identify the independent and dependent variables
Independent variable = blade angle / °
Dependent variable = voltage / V
Step 2: Choose an appropriate scale
The range of the blade angle is 0 – 90°
Ideally, every small square represents 10°
The range of the voltage is 0 – 2.2 V
Ideally, each small square represents 0.5 V
Both axes should occupy at least 50% of the grid
Step 3: Label the axes
The dependent variable (voltage / V) goes on the y-axis
The independent variable (blade angle / °) goes on the x-axis
Both axes should be labelled with a quantity and a unit
Step 4: Plot the points
Each point should be accurate within half a small square

Step 5: Draw a curve of best fit
The curve should be smooth with a roughly equal distribution of points on either side of the curve
It must start at (0,0) and peak at (20, 2.2)


Unlock more, it's free!
Did this page help you?