Radius of a Charged Particle in a Magnetic Field (Edexcel A Level Physics)

• A charged particle in uniform magnetic field which is perpendicular to its direction of motion travels in a circular path
• This is because the magnetic force F is always perpendicular to its velocity v
  • F will always be directed towards the centre of orbit

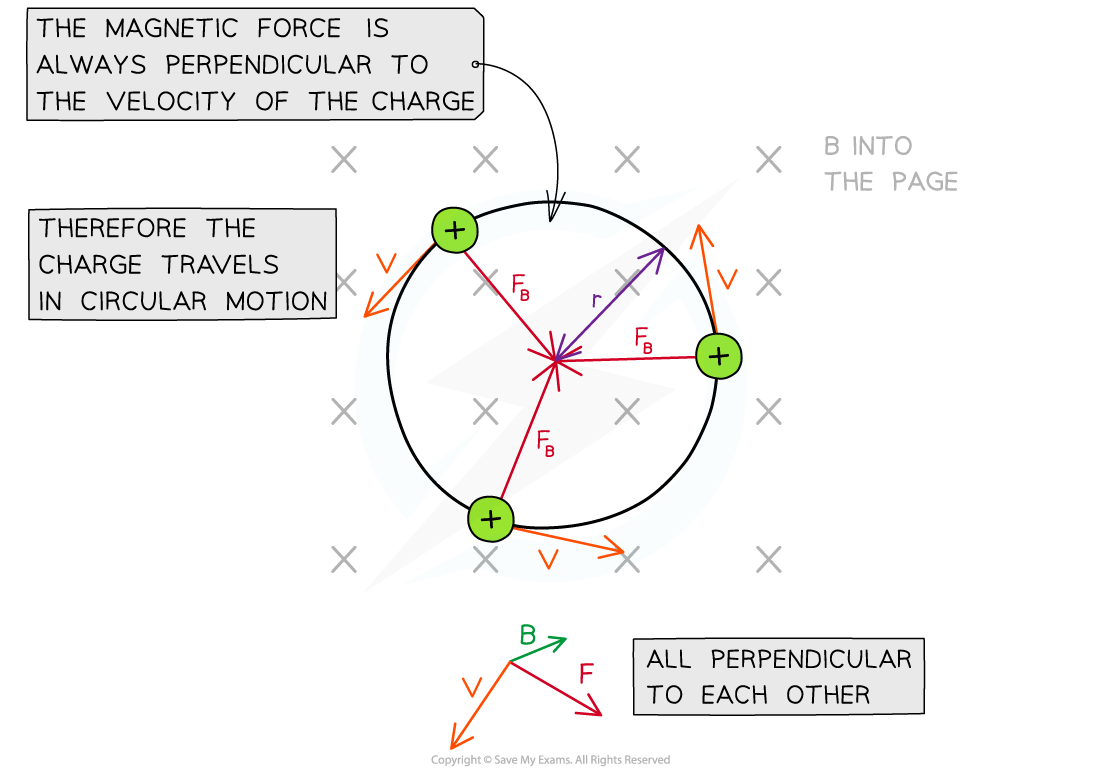
A charged particle travels in a circular path in a magnetic field

• The magnetic force F provides the centripetal force on the particle
• The equation for centripetal force is:

• Where:
  • F = centripetal force (N)
  • m = mass of the particle (kg)
  • v = linear velocity of the particle (m s^–1)
  • r = radius of orbit (m)

• Equating this to the magnetic force on a moving charged particle gives the equation:

• Rearranging for the radius r obtains the equation for the radius of the orbit of a charged particle in a perpendicular magnetic field:

• The product of mass m and velocity v is momentum p
  • Therefore, the radius of the charged particle in a magnetic field can also be written as:

• Where:
  • r = radius of orbit (m)
  • p = momentum of charged particle (kg m s^–1)
  • B = magnetic field strength (T)
  • q = charge of particle (C)

• This equation shows that:
  • Particles with a larger momentum (either larger mass m or speed v) move in larger circles, since r ∝ p
  • Particles with greater charge q move in smaller circles: r ∝ 1 / q
  • Particles moving in a strong magnetic field B move in smaller circles: r ∝ 1 / B