Root-Mean-Square Current & Potential Difference (Edexcel A Level Physics) : Revision Note
Root-Mean-Square Current & Potential Difference
The root-mean-square (rms) current Irms is defined by the equation:
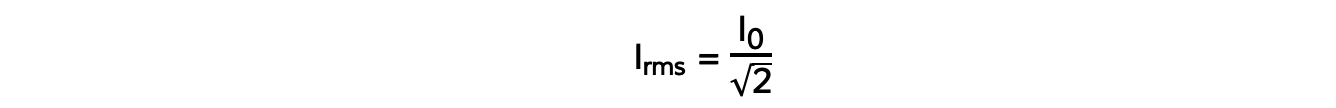
Where:
I0 = peak current (A)
The rms voltage Vrms is defined by the equation:

Where:
V0 = peak voltage (V)
Rms current is equal to 0.707I0, which is about 70% of the peak current I0
This is also the case for rms voltage
Worked Example
An electric oven is connected to a 230 V root mean square (rms) mains supply using a cable of negligible resistance.
Calculate the peak-to-peak voltage of the mains supply.
Answer:
Step 1: Write down the Vrms equation

Step 2: Rearrange for the peak voltage, V0
V0 = √2 × Vrms
Step 3: Substitute in the values
V0 = √2 × 230
Step 4: Calculate the peak-to-peak voltage
The peak-to-peak voltage is the peak voltage (V0) × 2
Peak-to-peak voltage = (√2 × 230) × 2 = 650.538 = 651 V (3 s.f)
Examiner Tips and Tricks
You are expected to know how to apply these equations, which simply relate the peak current or voltage of an AC circuit to its rms value.
Remember, the rms value in an AC circuit is equivalent to values of current and voltage that would produce the same heating effect in DC circuits. This means, you can use the rms values in AC circuits for equivalent calculations involving DC circuits.

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
