Revision NotesExam QuestionsPast Papers
A LevelPhysicsEdexcelRevision Notes5. Waves & Particle Nature of LightRefraction, Reflection & Polarisation5.23 Magnification

Magnification (Edexcel A Level Physics)

Revision Note

Lindsay Gilmour

Last updated

Magnification

Magnification as a Ratio of Heights

  • Magnification means how much larger the image is than the object
    • This is the ratio of the image/object height

m space equals h subscript i over h subscript o

  • Where:
    • m = magnification
    • hi = image height (m)
    • ho = object height (m)

Magnification as a Ratio of Distances

  • A diagram of an object and its real image will produce similar triangles
    • Therefore, the ratio of magnification is also represented by comparing distance from the lens to the object and the image

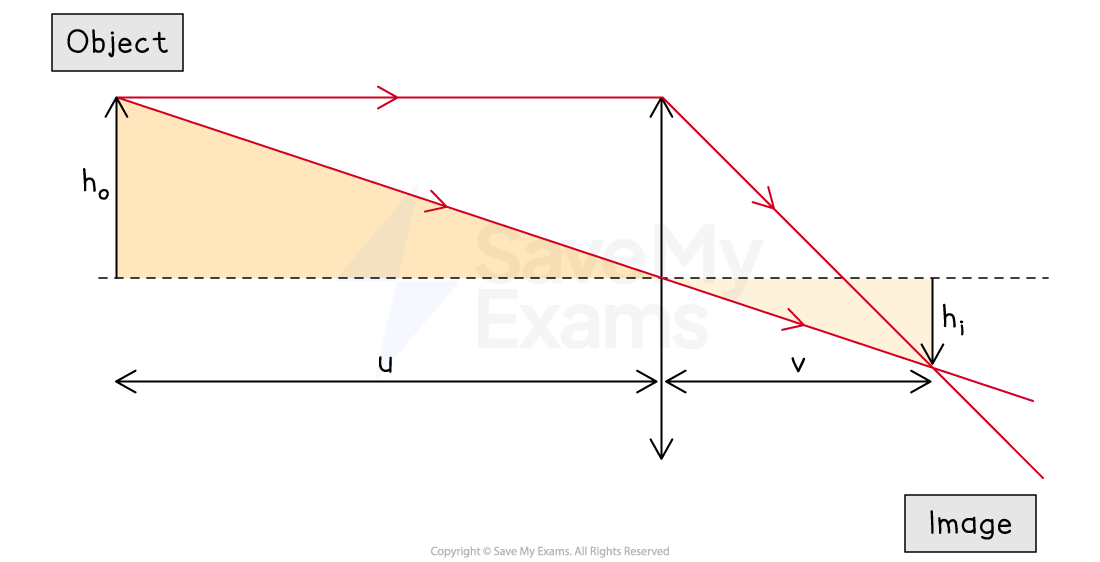
5-23-magnification-derivation-edexcel-al-physics-rn-1

  • This also works for virtual images

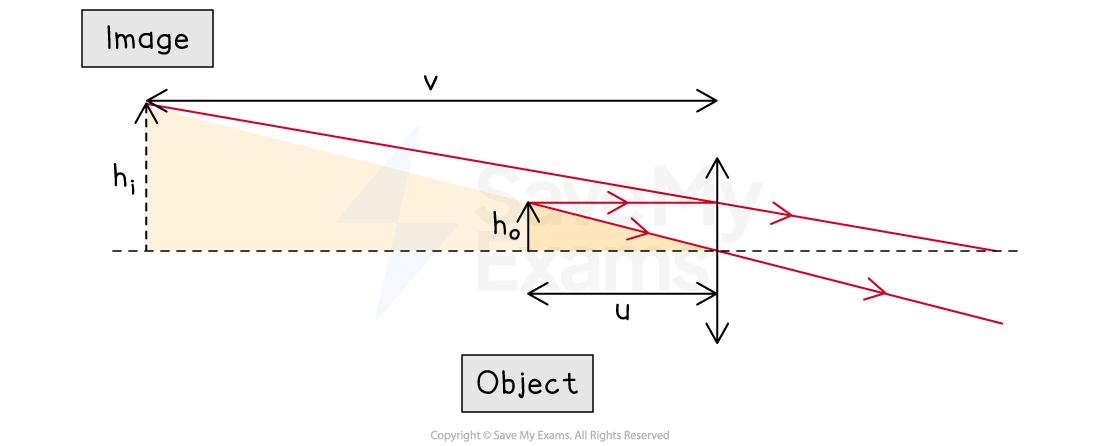
5-23-magnification-derivation-2_edexcel-al-physics-rn

 m space equals v over u

    • Where:
      • m = magnification
      • v = distance from lens to image (m)
      • u = distance from lens to object (m)
  • Since magnification is a ratio, it has no units

Worked example

A magnifying glass has a focal length of 15 cm. It is held 5 cm away from a component which is being examined. 

Determine the magnification of the image.

Step 1: Write the known values

    • Focal length, f = 15 cm
    • Distance between object and lens, u = 5 cm

Step 2: Use the lens formula and rearrange to make v the subject

1 over f equals 1 over u plus 1 over v

v equals open parentheses 1 over f minus 1 over u close parentheses to the power of negative 1 end exponent space open parentheses 1 over 15 minus 1 fifth close parentheses to the power of negative 1 end exponent space equals space minus space 7.5 space c m

    • The negative sign indicates a virtual image (expected for a magnifying glass) and is ignored for the next step

Step 3: Use the magnification formula to find the magnification of the image

m equals v over u space equals fraction numerator 7.5 over denominator space 5 end fraction space equals space 1.5

Worked example

A person sees an image from a magnifying glass.Magnification Worked Example Questions, downloadable IGCSE & GCSE Physics revision notesCalculate the magnification of this image. Clearly show your working on the diagram.

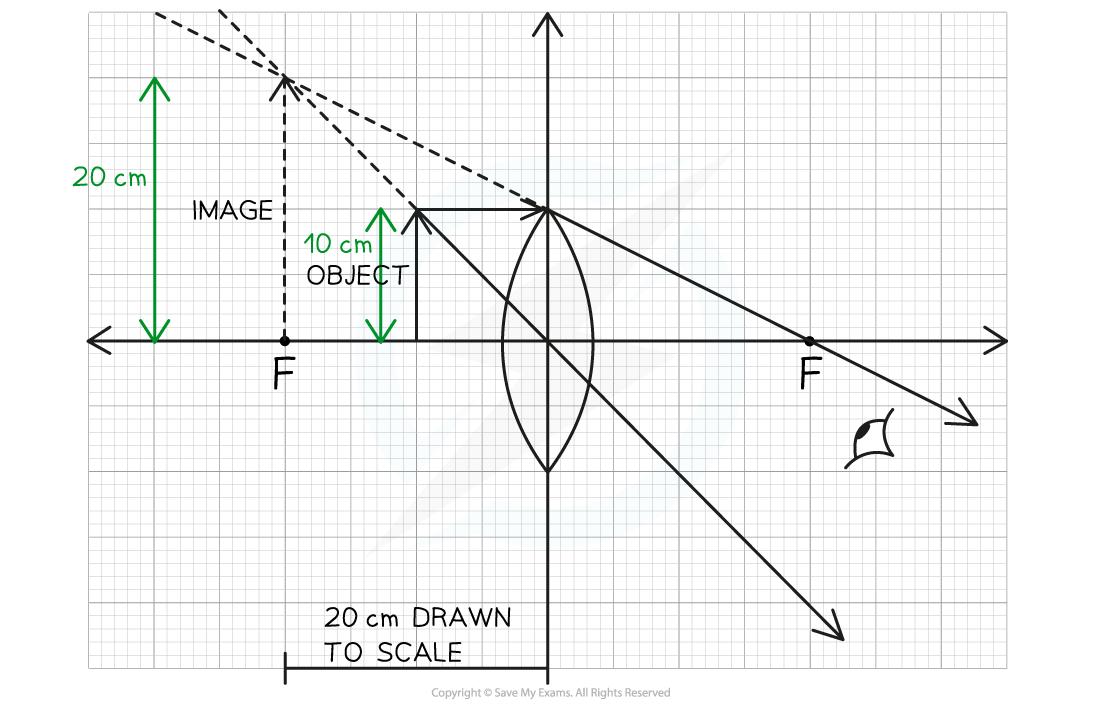
Magnification Worked Example Solution, downloadable IGCSE & GCSE Physics revision notes

Step 1: Measure the height of the object from the scale

The object is 10 cm

Step 2: Measure the height of image from the scale

The image is 20 cm

Step 3: Substitute values into the magnification equation

Examiner Tip

The most common mistake with magnification calculations is to get the formula upside down.

Do a 'sanity check' by looking at the answer to make sure that magnified objects have got bigger (m > 1) and diminished ones smaller (m < 1).

Since we are working with ratios (so the units get cancelled out) this is one of those rare times when you don't need to convert everything to SI units, but do check that your units are all the same - for example all distances in cm.

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:5.22 The Lens EquationNext:5.24 Plane Polarisation
    Lindsay Gilmour

    Author: Lindsay Gilmour

    Expertise: Physics

    Lindsay graduated with First Class Honours from the University of Greenwich and earned her Science Communication MSc at Imperial College London. Now with many years’ experience as a Head of Physics and Examiner for A Level and IGCSE Physics (and Biology!), her love of communicating, educating and Physics has brought her to Save My Exams where she hopes to help as many students as possible on their next steps.