Fig. 1.1 shows an incomplete extension–load graph obtained by adding multiple 1.0 N weights to a spring and recording the extension.
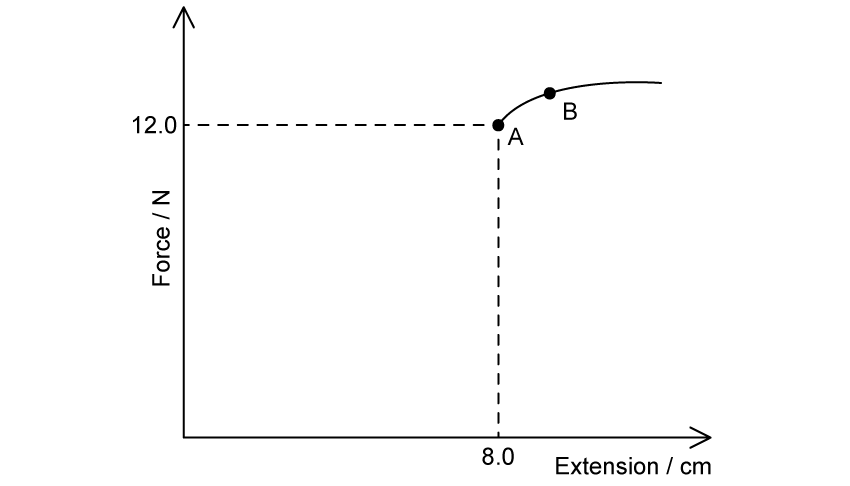
Fig. 1.1
The spring obeys Hooke’s law up to point A.
Draw a suitable line on Fig. 1.1 to show the relationship between force and extension up to point A.
State the relevance of point A.
Use Fig. 1.1 to calculate the energy stored in the spring when it is extended 8.0 cm. Show your working clearly.
Fig. 1.1 shows the spring exhibits elastic deformation up to point B.
(i) State the name given to point B.
[1]
(ii) Explain what is meant by elastic deformation.
[2]
Did this page help you?














