Define the following
(i) moment of a force
[2]
(ii) centre of gravity.
[1]
A teacher sets some Physics students the task of finding the weight of a broom using only a ruler, some thin, light string, and a set of laboratory masses. The equipment is initially arranged as shown in Fig. 1.1.
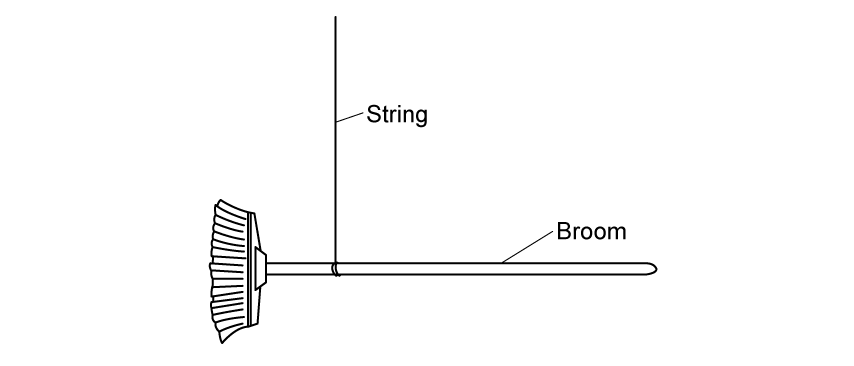
Fig. 1.1.
The students are not allowed to use scales.
For the arrangement in Fig. 1.1.
(i) State why the broom is hanging horizontally.
[2]
(ii) State what measurement the students should make to start their investigation to find the weight of the broom.
[1]
The measurement to the position of the string found in part (b) is shown in Fig. 1.2.
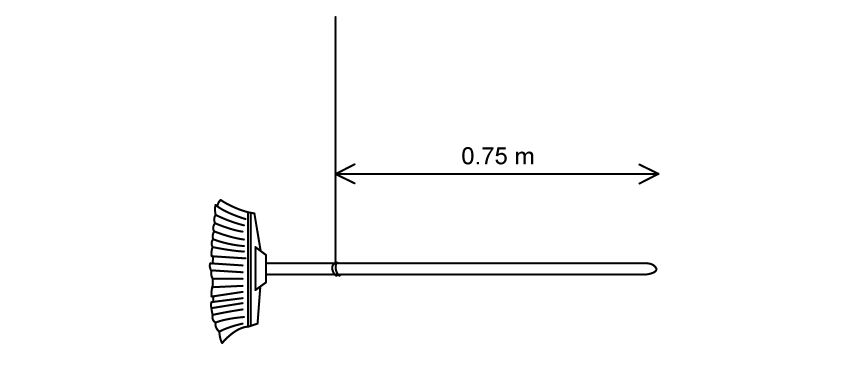
Fig. 1.2.
Distance from string to the end of the handle = 0.75 m
The string is moved towards the end of the handle, so that the broom is in equilibrium when a 0.5 kg mass is hung a distance of 0.45 m from the string as shown in Fig. 1.3.
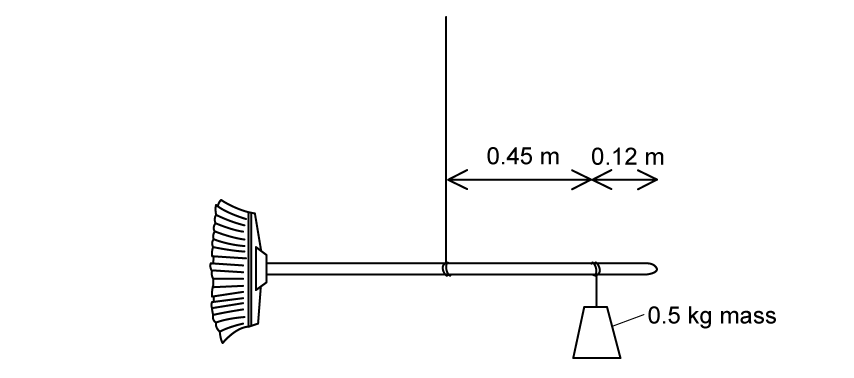
Fig. 1.3
Determine
(i) the distance between the centre of mass of the broom and the point where the string is attached.
[1]
(ii) the force exerted by the 0.5 kg mass.
[1]
Calculate the weight of the broom.
Did this page help you?












