Linear Momentum & its Conservation (CIE A Level Physics)

A ball X of mass 140 g travelling at constant velocity v collides head-on with a stationary ball Y of mass 620 g, as shown in Fig. 1.1.

After the collision, ball X comes to a stop. Ball Y moves off in the same initial direction as X with a velocity of 0.8 m s⁻¹.

Determine the velocity v of ball X before the collision.

The balls are replaced by an aluminium sphere of mass 2.7 kg and a steel sphere of 7.9 kg as shown in Fig. 1.2.

The aluminium sphere has an initial velocity of 10.0 m s^–1 when it collides with the stationary steel sphere. Immediately after the collision, the velocity of the steel sphere is 5.1 m s^–1.

Calculate the velocity v of the aluminium sphere immediately after the collision.

Verify that the collision in (c) is elastic.

Two identical blocks A and B each of mass 400 g are travelling towards each other along a straight line through their centre, as shown in Fig. 1.1.

Both blocks are moving at a speed of 0.36 m s^–1 relative to the surface.

As a result of the collision, the blocks reverse their direction of motion and travel at the same speed as each other. During the collision, 33% of the kinetic energy of the blocks is transferred to the surroundings as thermal energy.

Calculate the final speed of the blocks.

The duration of the collision between the blocks is 750 ms.

Determine the average force exerted by one block on the other.

The same blocks are investigated with different initial speeds. Block A is launched towards B at a speed of 0.6 m s⁻¹ and B is launched towards A at a speed of 0.4 m s⁻¹.

Once the blocks collide, they stick together and move as one after the collision.

Determine the speed of the combined blocks after the collision and state the direction.

A fast-moving asteroid B collides with a slower-moving asteroid A as shown in Fig. 1.1. Asteroid B becomes embedded within asteroid A as shown.

Before the collision, asteroid A had a velocity of 3.61 km s⁻¹ and a momentum of 2.00 × 10¹⁷ kg m s⁻¹.

Calculate the combined velocity, in km s⁻¹, of the asteroids after the collision.

mass of asteroid B = 6.40 × 10¹² kg
velocity of asteroid B before the collision = 14.0 km s⁻¹

A short time later, the combined asteroid AB collides with a stationary asteroid C. Immediately following the collision, the asteroids are deflected by the angles shown in Fig. 1.2.

Show that the mass of asteroid C is about 1.0 × 10¹³ kg.

Determine if the collision in (c) is elastic or inelastic.

Ball X has a mass of 50 g and is supported by a long string, as shown in Fig. 1.1.

Fig. 1.1

The ball is pulled back and released. The ball collides normally with a flat surface at a velocity of 4.5 m s⁻¹ and rebounds elastically.

The positive direction is horizontal and to the right.

Determine the total change in momentum of ball X. 

Ball X is hung next to ball Y which is supported by a string of the same length, as shown in Fig. 1.2.

Fig. 1.2

Ball Y has a mass of 125 g.

The balls are each pulled back and pushed towards each other. When the balls collide, the strings are vertical. The balls rebound in opposite directions.

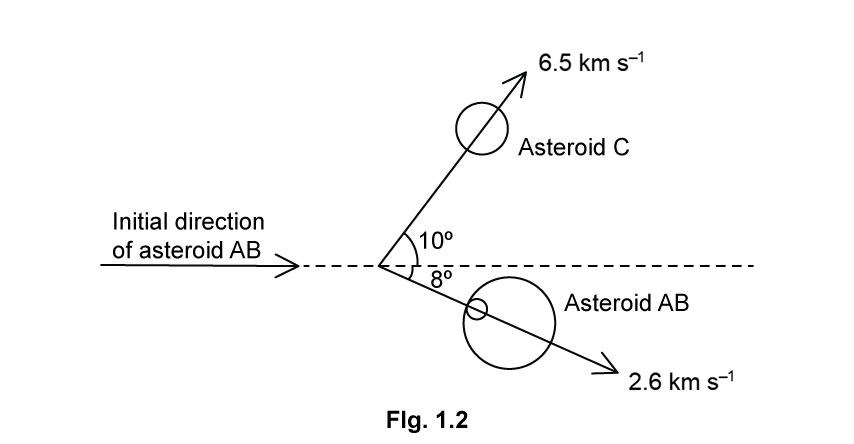
The velocities of X and Y just before and just after the collision are shown in Fig. 1.2.

Use the conservation of linear momentum to determine the rebound velocity  of Y.

Deduce whether the collision, in part (b), is elastic or inelastic.

Use Newton’s laws to explain why the magnitude of the change in momentum of each ball is the same.

A shell of mass 30 g is fired from the barrel of a rifle of mass 1.9 kg. Immediately after being fired, the bullet has a momentum of 36 kg m s⁻¹.

State the total momentum of the rifle and the bullet before the rifle is fired and give a reason for your answer.

Calculate the velocity of the shell just after the rifle is fired.

The shell has a momentum of 9.8 kg m s⁻¹ just before it hits a target.

It takes 4.5 ms for the bullet to the stopped by the target.

Calculate the average force needed to stop the bullet.

A stationary firework explodes into three different fragments that move in a horizontal plane. Fig. 1.1. shows the masses and velocities of the fragments A, B and C in terms of M and v.

Fig. 1.1

Use the principle of conservation of momentum to determine the speed of fragment B in terms of v.

Use the principle of conservation of momentum to determine the angle θ.

Another stationary firework explodes into four fragments which travel in different directions in a horizontal plane.

Fig. 1.2 shows the velocity and mass of each fragment.

Fig. 1.2

the velocity 

the mass 

Both fireworks have the same initial mass and release the same amount of kinetic energy.

[3]

Challenge

A firework similar to the one in (c) explodes into four fragments.

Fig. 1.3 shows the velocity and mass of each fragment.

Fig. 1.3

[6]

Hence, determine the values of , ,  and .

A pellet of mass 2.7 g is fired into a stationary block of mass 540 g suspended from a rigid support as shown in Fig. 1.1.

The pellet becomes completely embedded in the block. The block can swing freely at the end of a light inextensible string of length 1.5 m measured from the pivot to the centre of the block. 

Fig. 1.1

The centre of mass of the block rises by a height h at an angle of 35° to the vertical. 

Determine the velocity of the pellet and the block immediately after the pellet is embedded.

Calculate the velocity of the pellet just before it strikes the block. 

The block is replaced by a metal block of the same mass. The experiment is repeated with the wooden block and an identical pellet. The pellet rebounds after striking the block.

A student makes an assumption that the angle that the metal block makes with the vertical will be greater than 35° because the block doesn’t have the additional mass of the pellet embedded within it.

Discuss the validity of the student's assumptions.

A popular demonstration of the conservation of momentum and conservation of energy is Newton’s cradle. It features several identical polished steel balls hung in a straight line in contact with each other, as shown in Fig. 1.2.

If one ball is pulled back and allowed to strike the line, one ball is released from the other end whilst the rest are stationary. If two are pulled out, two are released on the other end and so forth.

Fig. 1.2

Explain why swinging one ball from the left will not release two balls on the right. 

Assume that the demonstration takes place in a vacuum.

A body of mass and moving with velocity  explodes into three equal fragments each of mass , as shown in Fig. 1.1.

Fig. 1.1

Fragment 2 continues to move along the horizontal plane with velocity , while fragments 1 and 3 move off at an angle of 60° to the horizontal with velocities and respectively, as shown. 

By applying the principle of conservation of momentum in the vertical plane, show that 

By applying conservation of momentum in the horizontal plane, show that 

The ratio of the kinetic energy of fragment 1 to mass M is

Express velocities and in terms of the velocity of mass .