A LevelPhysicsCIEExam Questions20. Magnetic Fields20.2 Force on a Current-Carrying Conductor

Syllabus Edition

First teaching 2023

First exams 2025

|

Force on a Current-Carrying Conductor (CIE A Level Physics)

Exam Questions

38 mins5 questions
Easy
Medium
1a
Sme Calculator4 marks

A long straight wire passes through a piece of card. There is a current in the wire, as shown in Fig. 1.1a.

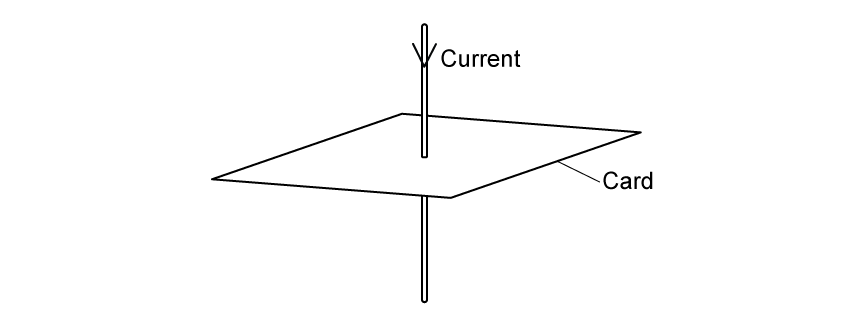
20-1-1a-e-20-1--e-magnetic-field-around-a-wire-1-cie-ial-sq

Fig. 1.1a

The current in the wire produces a magnetic field around the wire.

(i)
Fig. 1.1b shows the view of the card from above. On Fig. 1.1b, draw the magnetic field around the wire.
Show the direction of the magnetic field by drawing an arrow on each field line.

20-1-1a-e-magnetic-field-around-a-wire-2-cie-ial-sq

Fig. 1.1b

[2]

(ii)
Two identical wires with the same current pass through a different piece of card.
On Fig. 1.1c, draw the magnetic field around the wires.

20-1-1a-e-magnetic-field-around-two-wires-cie-ial-sq

Fig. 1.1c

[2]

How did you do?

1b
Sme Calculator4 marks

The current-carrying wire is placed in a uniform magnetic field. 

(i)
State the equation, and define all the variables, for the force on a current-carrying wire in a uniform magnetic field at different angles.
[2]
(ii)
Describe how the wire should be placed to experience 
1.  the maximum force due to the magnetic field
2.  no force due to the magnetic field.
[2]

How did you do?

1c
Sme Calculator2 marks

A current-carrying conductor placed at right angles to a uniform magnetic field which has a magnetic flux density of 15 × 10−3 T.

The conductor has a length of 1.2 m and a current of 1.5 A flowing through it.

Calculate the magnetic force acting on the conductor.

How did you do?

1d
Sme Calculator2 marks

The conductor is then rotated so that it is at an angle of 30° to the magnetic field.

Calculate the new force acting on the conductor.

How did you do?

Did this page help you?

2a
Sme Calculator3 marks

A current-carrying conductor at an angle θ to an external B field in Fig. 1.1. 

 

7-8-s-q--q1a-easy-aqa-a-level-physics

Fig. 1.1

 

F = BIL sin(θ) is used to calculate the force acting on the current-carrying conductor at different angles, θ, to the B field. 

State what the symbols B, I and L represent.

How did you do?

2b
Sme Calculator1 mark

State the angle, θ, between the conductor and the B field which would result in the largest force being exerted on the conductor.

How did you do?

2c
Sme Calculator1 mark

State the angle, θ, between the conductor and the B field which would result in there being no force exerted on the conductor from the B field.

How did you do?

2d
Sme Calculator2 marks

The conductor in Fig. 1.1 has a length of 1.5 m and has a current of 0.76 A flowing through it. The conductor is placed at 45o to the B field, which has a magnetic flux density of 40 mT. 

Calculate the force acting on the conductor.

How did you do?

Did this page help you?

1a
Sme Calculator1 mark

Fig. 1.1 shows a current-carrying conductor at an angle θ to an external B field.

  1a-figure-1

Fig. 1.1

   

The force acting on the current-carrying conductor when it lies at different angles to the field can be calculated using the equation

F space equals space B I L space sin space theta

 

State what the symbols B, I and L represent.

How did you do?

1b
Sme Calculator1 mark

State the angle, θ, between the conductor and the B field which would result in the largest force being exerted on the conductor.

How did you do?

1c
Sme Calculator1 mark

State the angle, θ, between the conductor and the B field which would result in there being no force exerted on the conductor from the B field.

How did you do?

1d
Sme Calculator2 marks

The conductor in the diagram in part (a) has a length of 1.2 m and a current of 0.85 A flowing through it. The conductor is placed at 30o to the B field, which has a magnetic flux density of 70 mT.

Calculate the force acting on the conductor.

How did you do?

Did this page help you?

2a
Sme Calculator1 mark

Define magnetic flux density.

How did you do?

2b
Sme Calculator1 mark

State the relationship between force and magnetic flux density when a current-carrying conductor is placed perpendicularly to an external magnetic field.

How did you do?

2c
Sme Calculator2 marks

Fig. 1.1 shows a wire of length 15 cm and mass 30 g which has a current of 2.0 A flowing through it. When the wire is placed perpendicular to a uniform magnetic field it 'floats' in equilibrium in the magnetic field.

   

q3c-figure-1

   

Determine the magnitude of the magnetic force acting on the wire when it is carrying current.

How did you do?

2d
Sme Calculator2 marks

Calculate the magnetic flux density required to keep the wire ‘floating’ in equilibrium.

How did you do?

Did this page help you?

3a
Sme Calculator1 mark

State the vector quantity that describes the number of magnetic field lines per unit area and its associated unit.

How did you do?

3b
Sme Calculator1 mark

Fig. 1.1 shows a current-carrying copper wire placed at right angles to an external magnetic field.

20-2-m-q3b-sq-cie-ial-physics

Fig. 1.1

The section of wire shown in the diagram has a length of 85 mm, a diameter of 1.1 mm, and a current of 0.42 A.

State the direction of the magnetic force acting on the moving electrons in the wire.

How did you do?

3c
Sme Calculator3 marks

Copper contains 8.4 × 1028 free electrons per cubic metre.

Show that there are about 7 × 1020 free electrons in this section of the wire.

How did you do?

3d
Sme Calculator3 marks

The average magnetic force acting on one electron is 5.5 × 10−24 N.

Use your answer from part (c) to determine the magnetic flux density of the magnetic field.

How did you do?

Did this page help you?