Define an oscillation.
Identify the correct definition by drawing lines between the properties of oscillations and their definition.
Properties of Oscillations | Definition of Properties |
Displacement | The rate of change of angular displacement with respect to time |
Amplitude | The distance of an oscillator from its equilibrium position |
Angular Frequency | The time taken for one complete oscillation |
Frequency | The maximum displacement of an oscillator from its equilibrium position |
Time Period | The number of oscillations per unit time |
Define simple harmonic oscillation.
Use the words in the box below to correctly label the diagram of an oscillating pendulum in Fig 1.1.
displacement of mass | mass | acceleration | restoring force | equilibrium position |
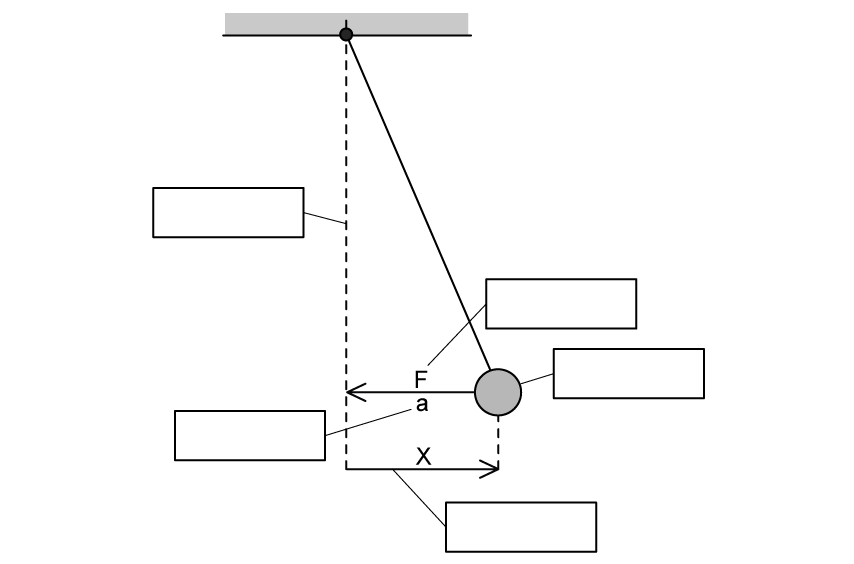
Fig. 1.1
Did this page help you?










