Ohm's Law (Cambridge (CIE) A Level Physics) : Revision Note
Ohm's law
Ohm’s law states that:
For a conductor at a constant temperature, the current through it is proportional to the potential difference across it
Constant temperature implies constant resistance
This is shown the equation below:
V = IR
V = potential difference (V)
I = current (A)
R = resistance (Ω)
The relationship between the potential difference across an electrical component (in this case a fixed resistor) and the current can be investigated through a circuit such as the one below
Investigating potential difference and current in a circuit

Circuit for plotting graphs of current against voltage
By adjusting the resistance on the variable resistor, the current and potential difference will vary in the circuit
Measuring the variation of current with potential difference through the fixed resistor will produce the straight line graph below
Plotting current against voltage
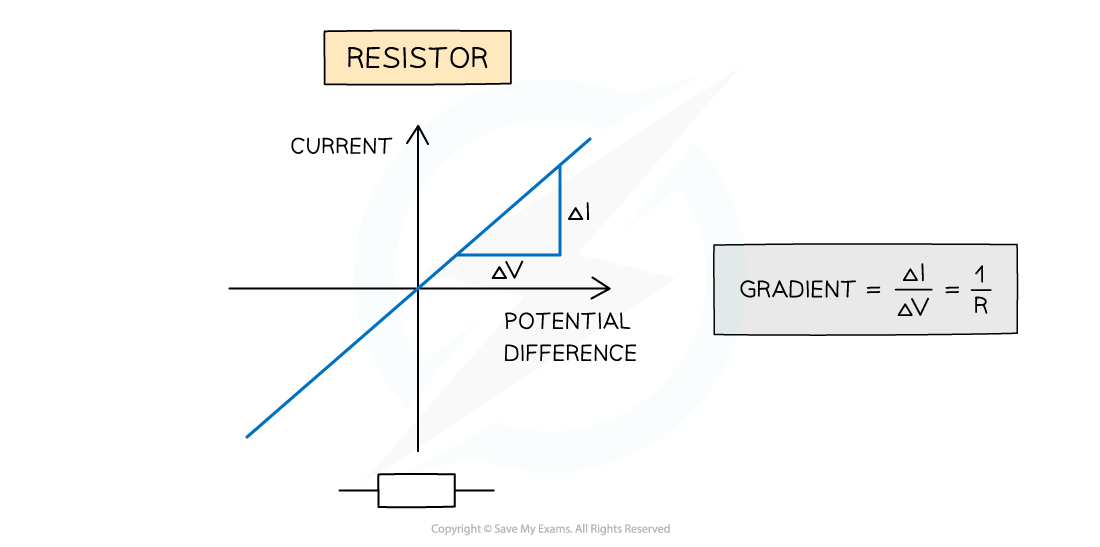
Circuit for plotting graphs of current against voltage.
Since the gradient is constant, the resistance of the resistor can be calculated by using 1 ÷ gradient of the graph
An electrical component obeys Ohm’s law if its graph of current against potential difference is a straight line through the origin
A resistor obeys Ohm’s law
A filament lamp does not obey Ohm’s law
This applies to any metal wires, provided that the current isn’t large enough to increase their temperature
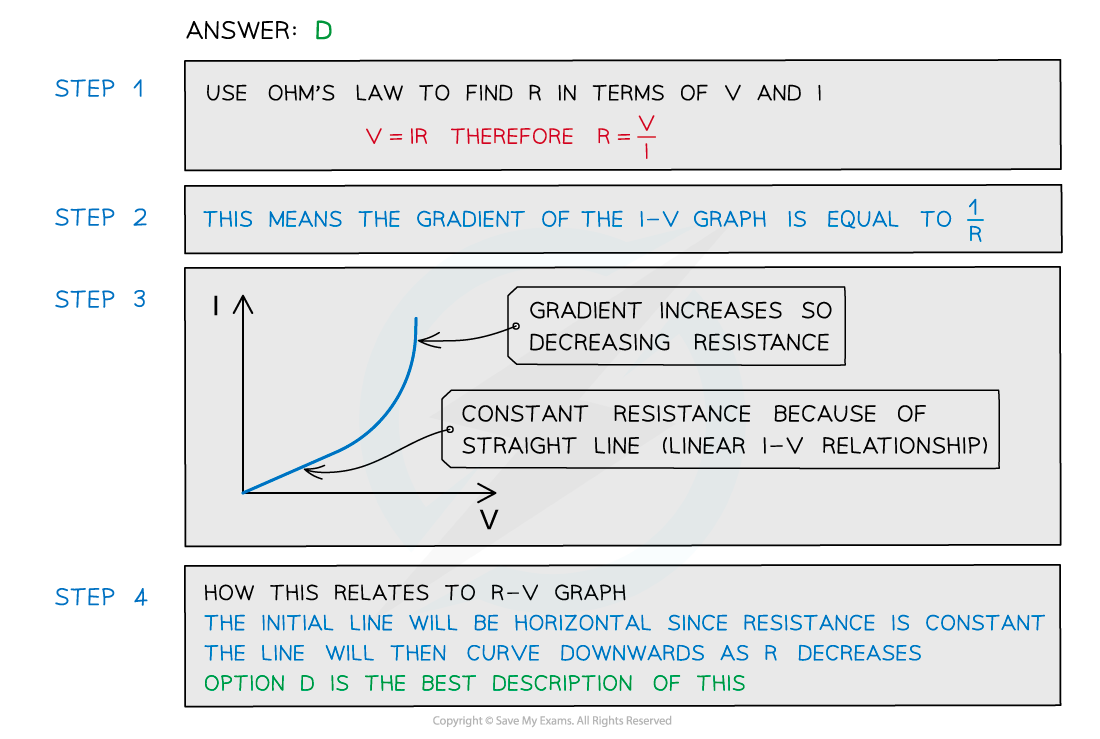
Worked Example
The current flowing through a component varies with the potential difference V across it as shown.

Which graph best represents how the resistance R varies with V?

Examiner Tips and Tricks
In maths, the gradient is the slope of the graph
The graphs below show a summary of how the slope of the graph represents the gradient
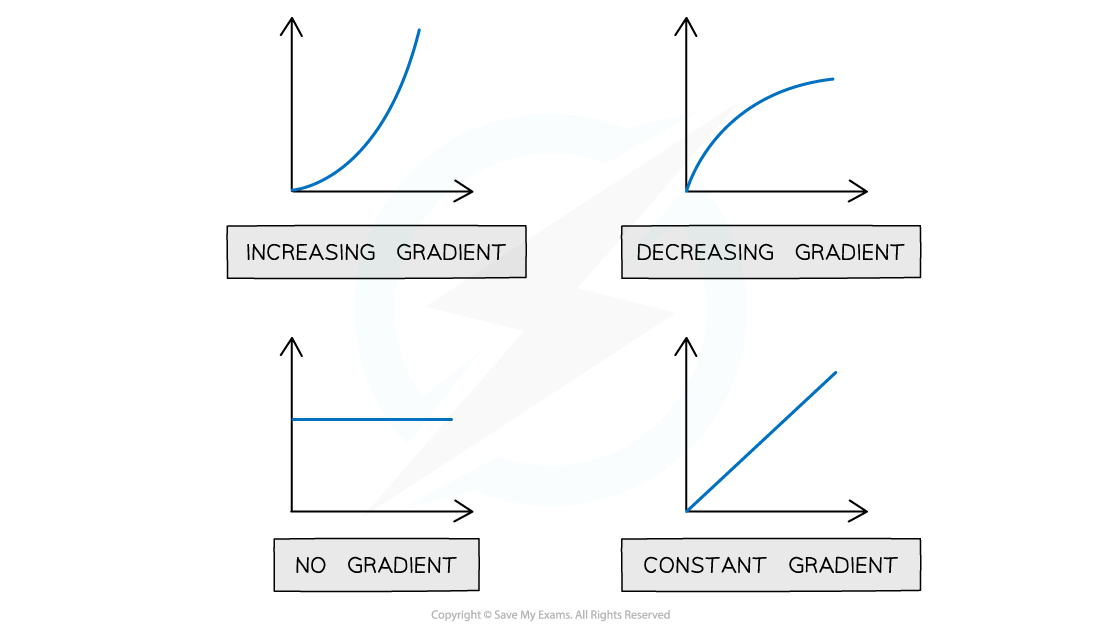
Graphs showing varying gradients

You've read 0 of your 5 free revision notes this week
Sign up now. It’s free!
Did this page help you?
