Polarisation (CIE A Level Physics)

Polarisation of transverse waves

• Transverse waves are waves that oscillate with their displacement perpendicular to their direction of travel
  • These oscillations can happen in any plane perpendicular to the propagation direction
• An electromagnetic wave is an example of a transverse wave that oscillates in more than one plane
  • A magnetic field oscillates on one plane
  • An electric field oscillates on a different plane
  • Both planes are at right angles to each other and to the direction of wave motion

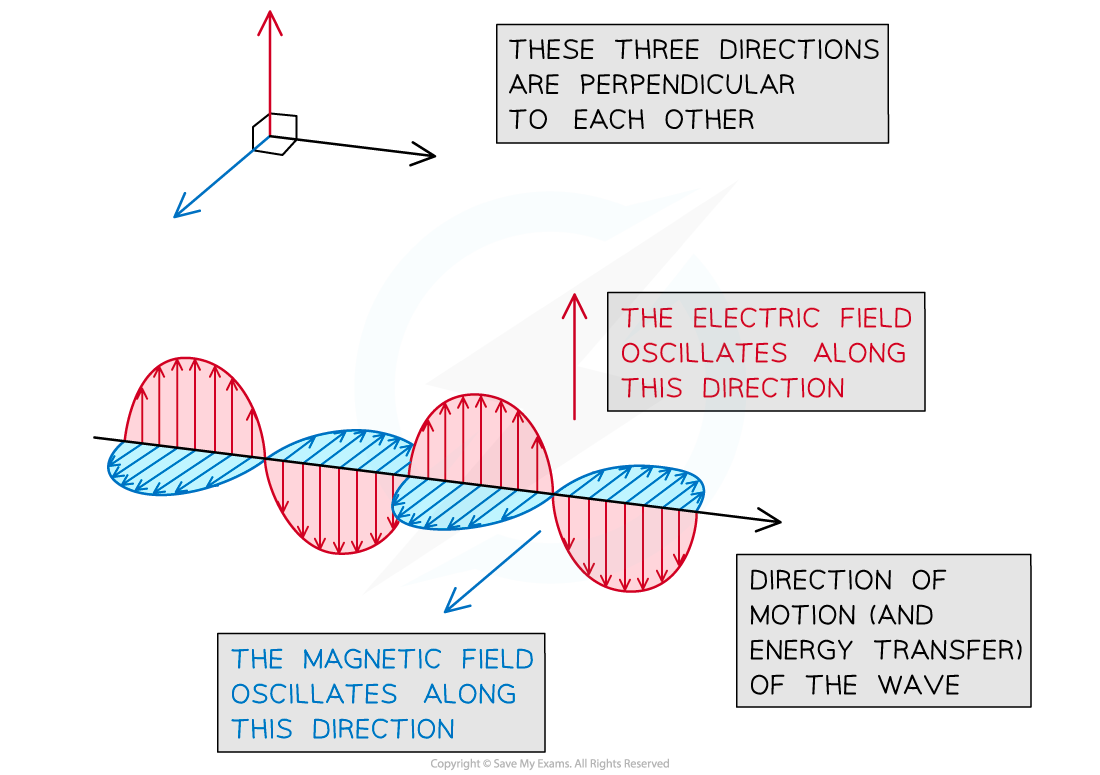
An electromagnetic wave is generated by the combined oscillation of an electric and a magnetic field

• When transverse waves are polarised
  • vibrations are restricted to one plane of oscillation
  • vibrations are still perpendicular to the direction of propagation / energy transfer

• The difference between unpolarised and polarised waves are shown in the diagram below
  
  • The blue arrows represent the direction of the plane of oscillation of the transverse wave
• An unpolarised wave oscillates in many planes of oscillation
• A vertically polarised wave oscillates only in the vertical plane
• A horizontally polarised wave oscillates only in the horizontal plane

Different planes of polarisation

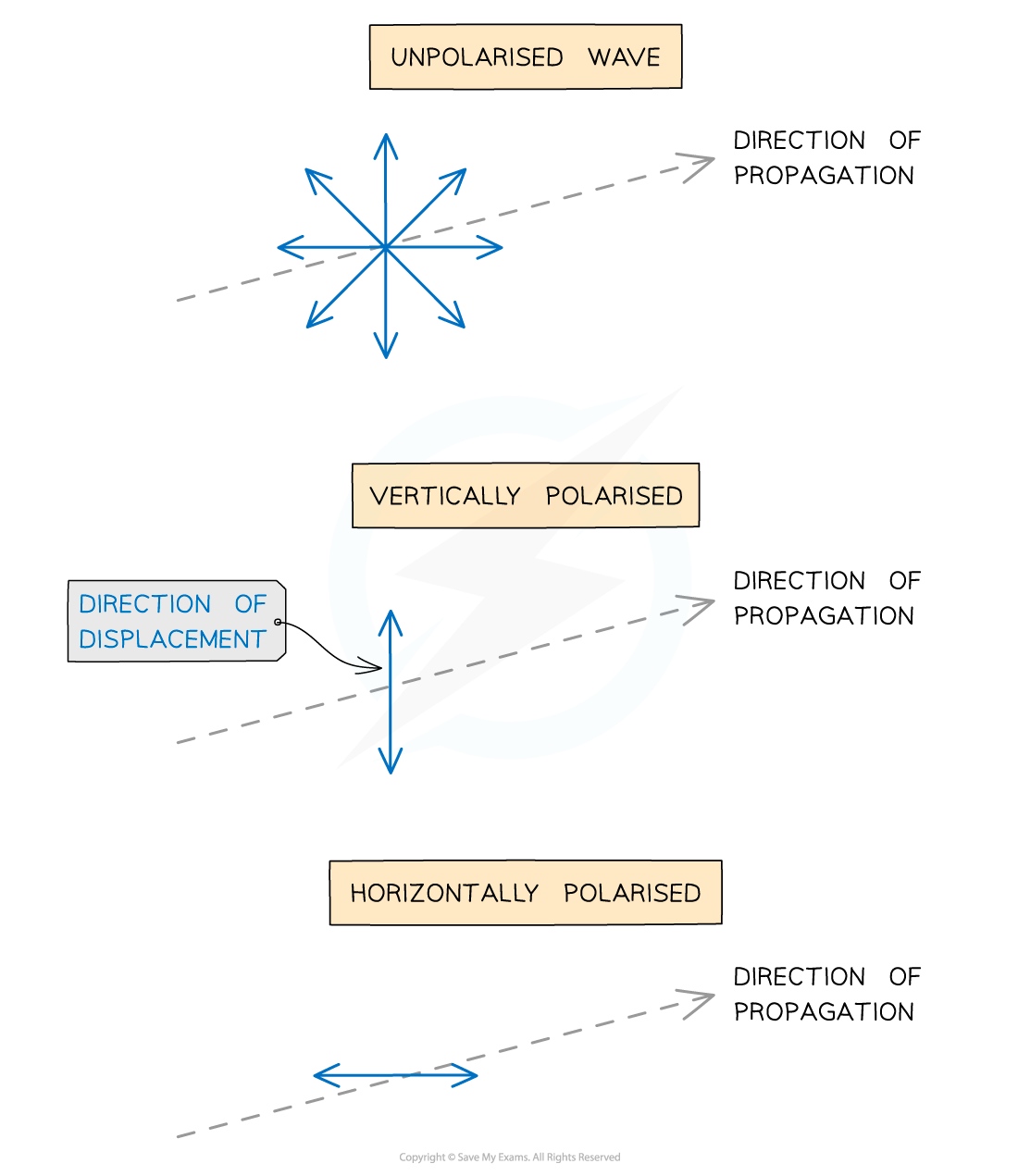
Diagram showing the displacement of unpolarised and polarised transverse waves

Polarising filters

• Waves can be polarised by passing through a polariser or polarising filter. 
  • Polarisers only allow oscillations in a certain plane to be transmitted through the filter
• A polariser is an optical layer or lens that consists of many parallel tiny slits
  • A polariser only allows waves vibrating parallel to the direction of these slits to pass through
  • Waves that are not orientated in the correct plane are blocked by the filter and do not pass through

 Action of a polarising filter

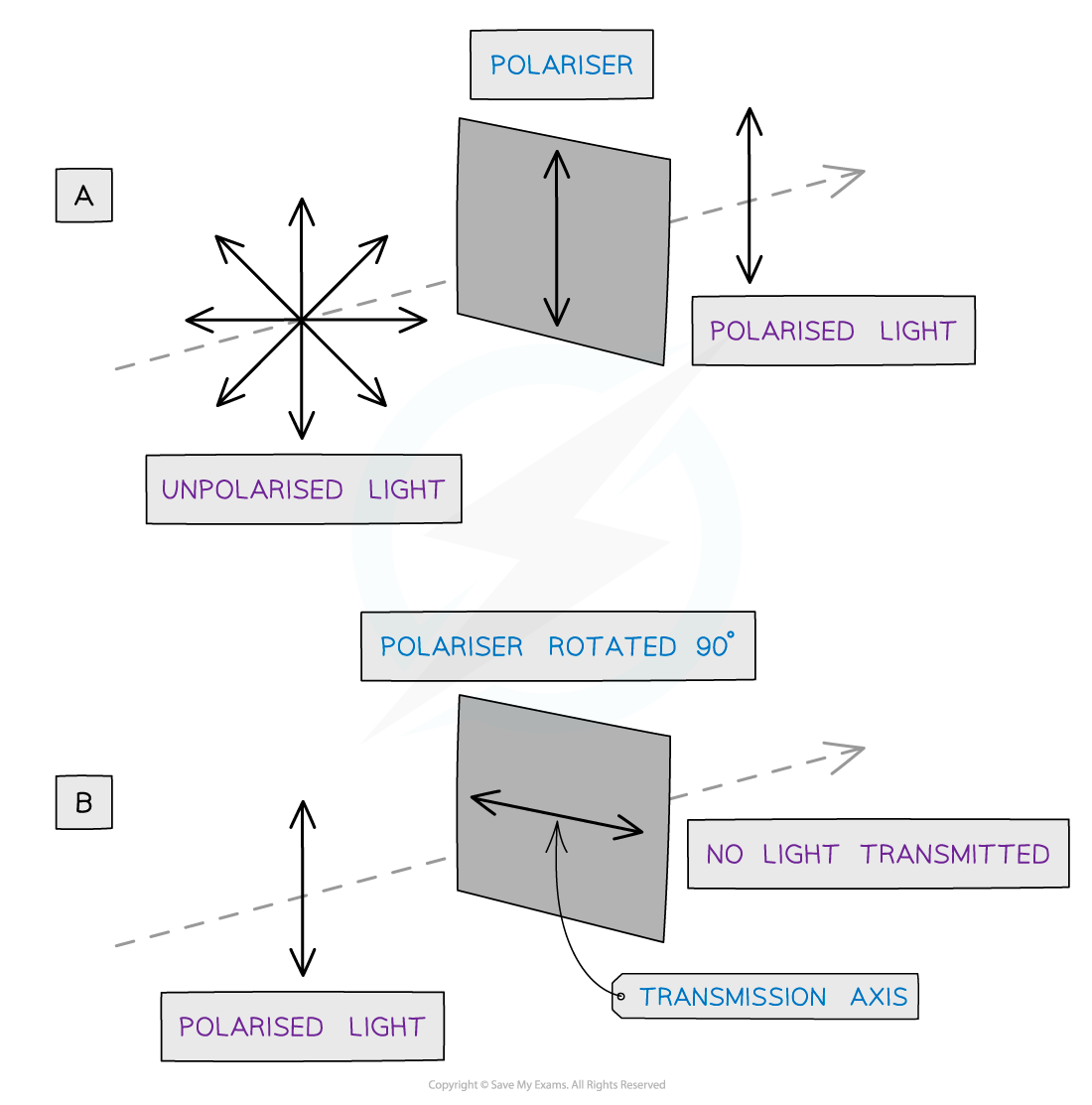
Diagram showing an unpolarised and polarised wave travelling through polarisers

• Only unpolarised waves can be polarised 
  • This is shown in diagram A
  • When a polarised wave passes through a filter with a transmission axis perpendicular to the wave (diagram B), none of the wave will pass through

Polaroid sunglasses

• Polaroid sunglasses are an example of a polarisation
• Polaroid sunglasses contain lenses with polarising filters with transmission axes that are vertically oriented
  • This means the glasses do not allow any horizontally polarised light to pass through

Polaroid sunglasses

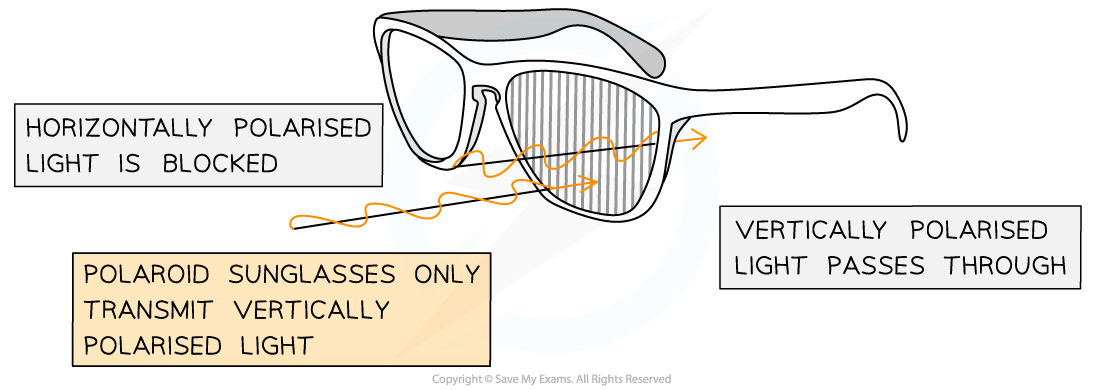
Polaroid sunglasses contain vertically oriented polarising filters which block out any horizontally polarised light

Intensity of polarised electromagnetic waves

• The intensity of electromagnetic waves is reduced as a result of polarisation
• If unpolarised electromagnetic waves of intensity I₀ pass through a polariser, the intensity of the transmitted polarised waves falls by a half
  •   is known as the half rule

Intensity of polarised and unpolarised light

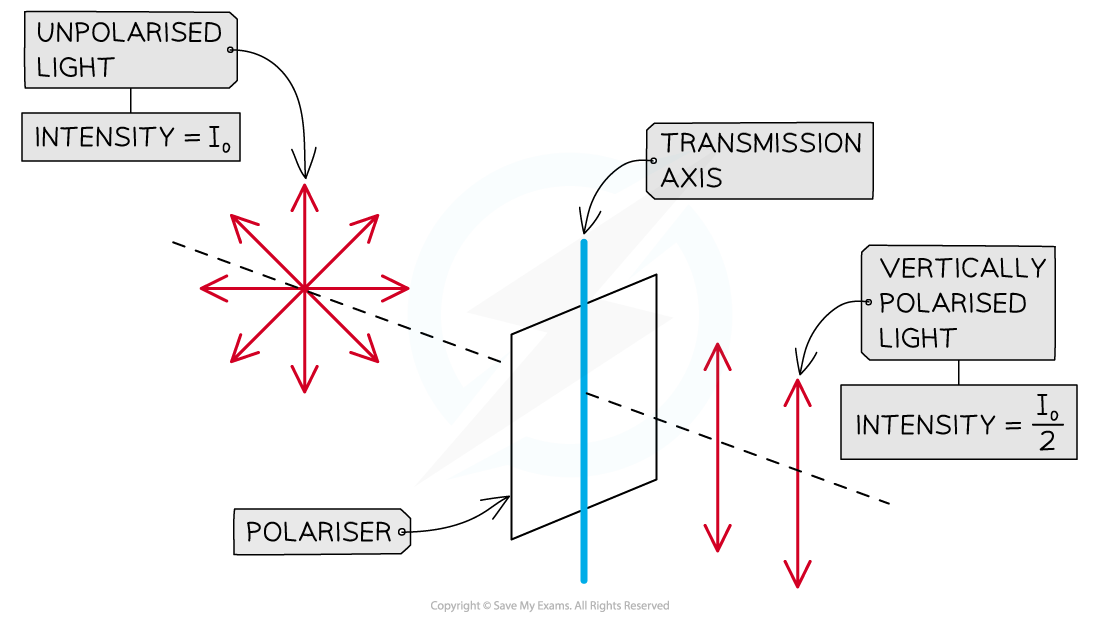
The intensity of polarised light transmitted by a polariser is half the intensity of the unpolarised light incident on it

Intensity of analysed electromagnetic waves

• A second polarising filter placed after the first is known as an analyser 

Intensity of waves when polariser and analyser have the same orientation

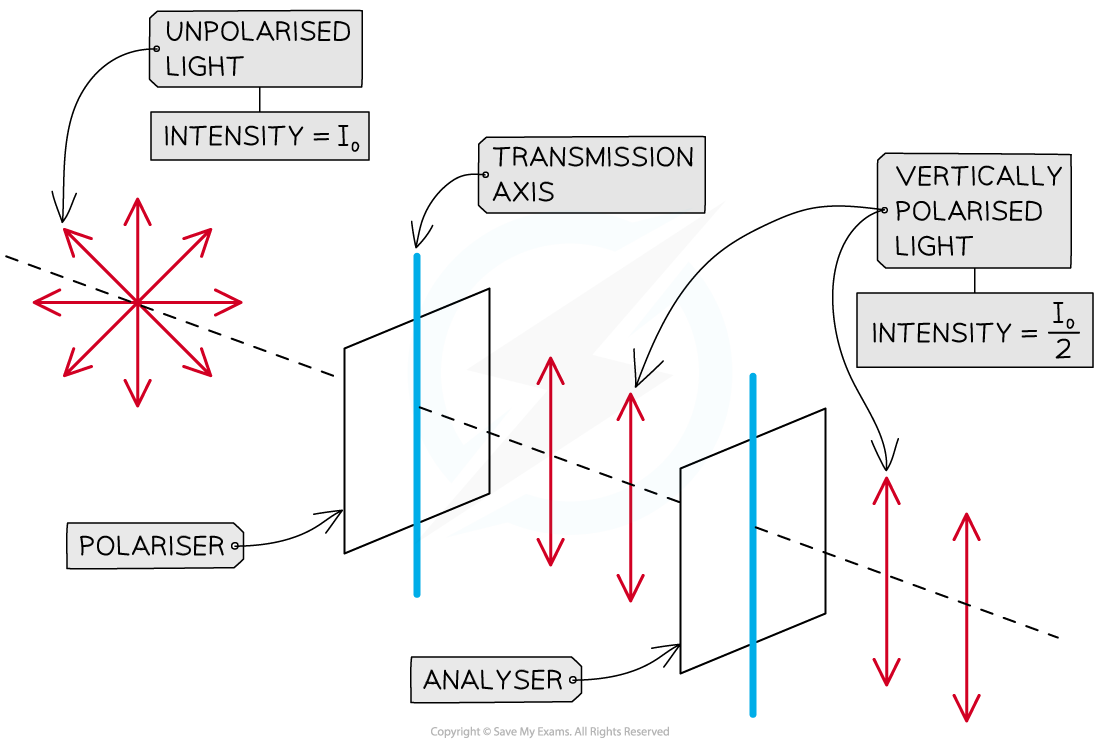
When the polariser and the analyser have the same orientation (i.e. parallel transmission axes), the intensity of analysed light is the same as the intensity of polarised light

Malus's law

• Malus's law states that if the analyser is rotated by an angle θ  with respect to the polariser, the intensity of the waves transmitted by the analyser is given by the equation

• Where
  • I is intensity of transmitted light in W m⁻²
  • I₀ is maximum intensity (same units)

• If the polariser and the analyser have the same orientation, electromagnetic waves transmitted by the analyser have the same intensity as waves that are incident upon it, since cos(0) = 1
  • If vertically polarised electromagnetic waves with intensity are incident on an analyser with a vertical transmission axis, all of the waves will be transmitted through the analyser 
  • The intensity between the polariser and the analyser will not decrease 

• If the analyser is rotated by 90° with respect to the polariser (θ = 90°), the intensity of the light transmitted by the analyser will be zero, since cos(90°) = 0
  • If vertically polarised light is incident on an analyser with a horizontal transmission axis, none of the light will be transmitted through the analyser
  • In this instance, all the waves will be absorbed

Table of transmission depending on polariser orientation