Syllabus Edition

First teaching 2023

First exams 2025

The Young Modulus (CIE A Level Physics)

Revision Note

Test yourself

Author

Katie M

Last updated

17 October 2024

Stress, strain & the Young modulus

Stress

Tensile stress is the applied force per unit cross sectional area of a material

$σ = \frac{F}{A}$

Where:
- σ is tensile stress in Pa
- F is applied force in N
- A is the cross-sectional area of the object in m²
The ultimate tensile stress is the maximum force per original cross-sectional area a wire is able to support at the point it breaks

Strain

Strain is the extension per unit length
- Strain is the deformation of a solid due to stress in the form of elongation or contraction
Note that strain, ε , is a dimensionless unit because it is the ratio of lengths given by the equation

$ε = \frac{x}{L}$

Where:
- x is extension in metres (m)
- L is the original length of the object, also in metres (m)

Young modulus

The Young modulus, E , is a measure of the ability of a material to withstand changes in length when a load is added
- Young modulus is a measure of how stiff or elastic a material is
The Young Modulus is defined as the ratio of stress and strain and is given by the equation

$E = \frac{σ}{ε} = \frac{F L}{A x}$

Where:
- E is Young modulus where its unit are the same as stress: Pa (since strain is unitless)
For a material demonstrating elastic behaviour, stress and strain, like force and extension, are also directly proportional to one another
The directly proportional nature of the stress-strain relationship can be shown by drawing a stress-strain graph
- The gradient of the linear section of a stress-strain graph is the Young modulus

Stress-strain graph

Stress-strain graph, downloadable AS & A Level Physics revision notes

A stress-strain graph is a straight line with its gradient equal to Young modulus

Worked example

A metal wire that is supported vertically from a fixed point has a load of 92 N applied to the lower end.

The wire has a cross-sectional area of 0.04 mm² and obeys Hooke’s law.

The length of the wire increases by 0.50%. What is the Young modulus of the metal wire?

A. 4.6 × 10⁷Pa

B. 4.6 × 10¹² Pa

C. 4.6 × 10⁹Pa

D. 4.6 × 10¹¹ Pa

Answer: D

Step 1: List the known quantities:

Load force, F = 92 N
Cross-sectional area, A = 0.04 mm²
Extension is 0.50% of the original length

Step 2: Determine the stress:

Convert the area to m²

$A = 0.04 {mm}^{2} = 0.04 (mm \times mm) = 0.04 (10^{- 3} m \times 10^{- 3} m)$

$A = 0.04 \times 10^{- 6} m^{2}$

Substitute this into the stress equation

$σ = \frac{F}{A} = \frac{92}{0.04 \times 10^{- 6}} = 2.3 \times 10^{9} Pa$

Step 3: Determine strain:

Strain is defined as the extension per unit length
If extension is 0.50% of length, then strain is simply this value as a decimal number

$ε = 0.50 % = \frac{0.50}{100} = 0.005$

Step 4: Calculate the Young modulus:

Substitute these values into the equation

$E = \frac{σ}{ε} = \frac{2.3 \times 10^{9}}{0.005} = 4.6 \times 10^{11} Pa$

Examiner Tip

To remember whether stress or strain comes first in the Young modulus equation, try thinking of the phrase ‘When you’re stressed, you show the strain’ i.e. $\frac{stress}{strain}$ .

Young's modulus experiment

Equipment

To measure the Young modulus of a metal in the form of a wire requires the wire to be clamped over a pulley as shown in the diagram below

Experimental equipment to determine the Young modulus

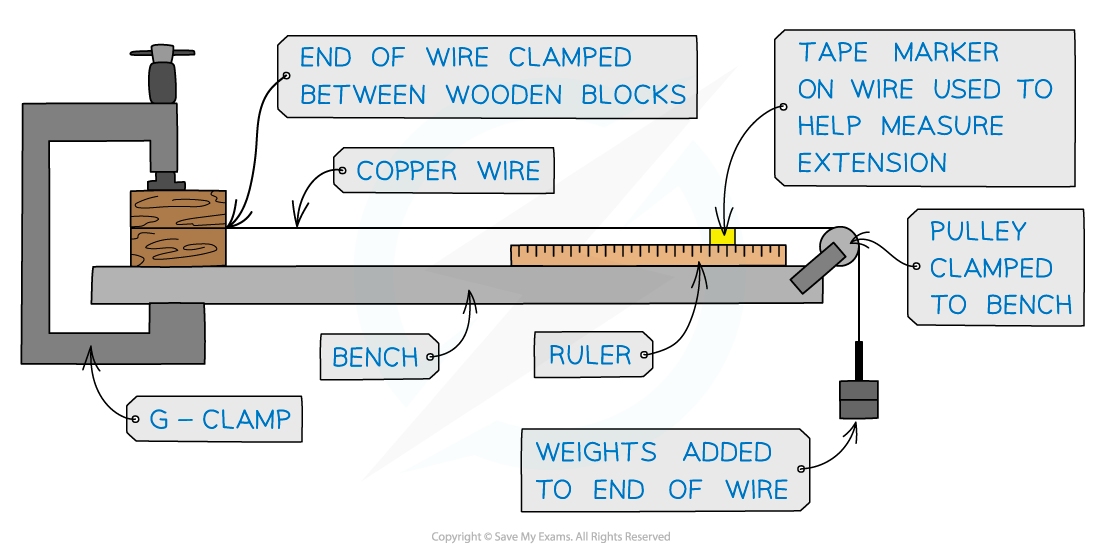
Apparatus, downloadable AS & A Level Physics revision notes

As the wire stretches, the tape marker moves along the ruler, showing the extension of the wire. This is based on the assumption that the wire stretches the same amount at all points along its length.

A tape or reference marker is needed on the wire to accurately measure the extension with the applied load
- The independent variable is the load
- The dependent variable is the extension

Method

Measure the original length of the wire using a metre ruler and mark this reference point with tape
Measure the diameter of the wire with a micrometre screw gauge or digital callipers
Add the first mass and calculate the weight used to create the extension e.g. 300 g
Record the total length from the reference point on the metre ruler
Add more mass and record the new total length from the metre ruler
Subtract the original length from the new total length to obtain the extension

Improving experiment and reducing uncertainties

Reduce uncertainty of the cross-sectional area by measuring the diameter d in several places along the wire and then calculating an average
After each reading remove the load and check that the wire returns to its original shape after each reading
Take several readings with each loads and find the average extension
Use a Vernier scale to measure the extension of the wire

Measurements required to determine the Young modulus

1. Determine extension from final and initial readings

Example table of results

Mass / kg	Load / N	Initial length / mm	Final length / mm	Extension / × 10⁻³ m
0.2	2.0	500	500.1	0.1
0.3	2.9	500.1	500.4	0.3
0.4	3.9	500.4	501.0	0.6
0.5	4.9	501.0	501.9	0.9
0.6	5.9	501.9	503.2	1.3
0.7	6.9	503.2	504.9	1.7
0.8	7.8	504.9	507.0	2.1

Table with additional data

QUANTITY / UNIT	SIZE
Length L / m	1.382
Diameter 1 / mm	0.277
Diameter 2 / mm	0.280
Diameter 3 / mm	0.275
Average diameter / mm	0.277

2. Plot a graph of force against extension and draw a line of best fit

3. Determine the gradient of the force-extension graph

Force-extension graph

Force extension graph results, downloadable AS & A Level Physics revision notes

This gradient is neither stress nor strain, but can be used to calculate Young's modulus

4. Calculate the cross-sectional area A of the wire from:

$A = \frac{π d^{2}}{4}$

where d is the average diameter of the wire

5. Calculate the Young modulus from:

$E = \frac{σ}{ε} = \frac{F L}{A x} = gradient \times \frac{L}{A}$

using the gradient of the force-extension graph, the initial length of the wire and it's average cross-sectional area

Examiner Tip

Although every care should be taken to make the experiment as reliable as possible, you will be expected to suggest improvements in producing more accurate and reliable results (e.g. repeat readings and use a longer length of wire)

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

Test yourself Next topic

Did this page help you?