Work & Energy | CIE International A Level Physics Revision Notes 2025

Work done

In physics, work is done when an object is displaced by an external force applied in the direction of its displacement

$W = F s$

Where:
- W = work done in newton metres (N m) or joules (J)
  - 1 N m = 1 J
- F = force in newtons (N)
- s = displacement of object in metres (m)

In the diagram below, the man’s pushing force on the block is doing work as it is transferring energy to the block (increasing its kinetic energy)

Man pushing a block

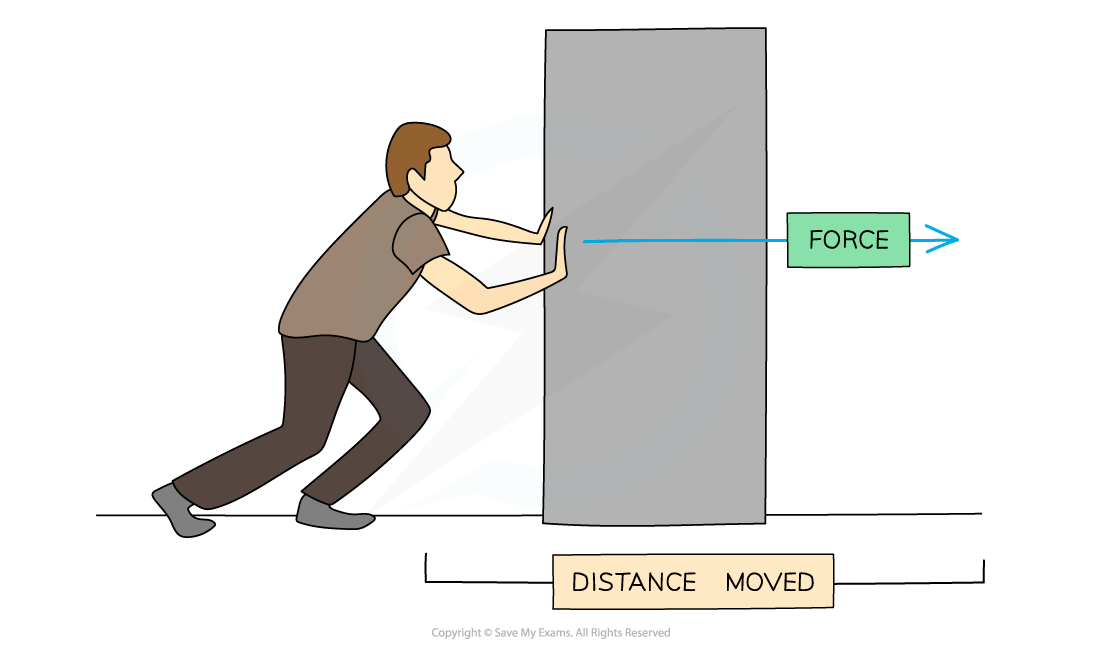
Work done diagram, downloadable AS & A Level Physics revision notes

Work is done when a force is used to move an object over a distance

When work is done, energy is transferred
Work done is equal to the amount of energy transferred
Usually, if a force acts in the direction that an object is moving, then the object will gain energy
If the force acts in the opposite direction to the movement, then the object will lose energy

Worked example

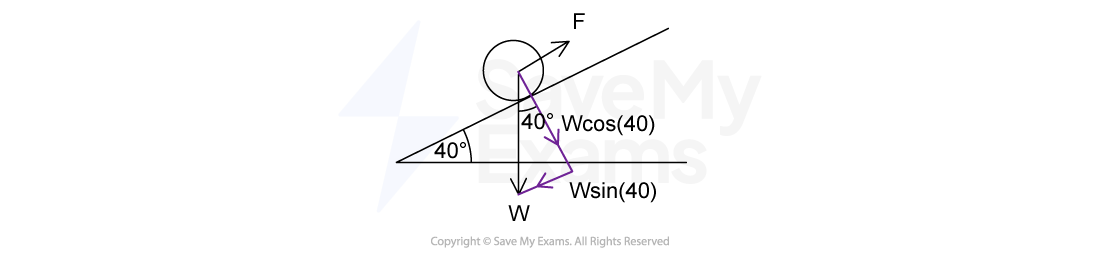
The diagram shows a barrel of weight 2.5 × 10³ N on a frictionless slope inclined at 40° to the horizontal.

WE - Work done on barrel question image, downloadable AS & A Level Physics revision notes A force is applied to the barrel to move it up the slope at constant speed.

The force applied is parallel to the slope.

How much work is done in moving the barrel a distance of 6.0 m up the slope?

A. 7.2 × 10³ J B. 2.5 × 10⁴ J C. 1.1 × 10⁴ J D. 9.6 × 10³ J

Answer:

Step 1: List the known quantities

Weight, F_W = 2.5 × 10³ N at 40°
- It is helpful to use F_W for the force of weight since W is used for work done
displacement, s = 6.0 m

Step 2: State the work done equation

$W = F s$

Step 3: Calculate the force in the direction of travel

The force, F_A, applied to push the barrel needs to overcome the component of the barrel's weight that is parallel to the slope
Since the force is parallel to the slope, the component of weight to consider is that which is parallel to the slope

5-1-1-we-work-done-on-barrel-answer-cie-new

$F_{A} = F_{W} \times \sin (40)$

$F_{A} = 2.5 \times 10^{3} \times \sin (40)$

$F_{A} = 1607 N$

Step 4: Substitute the known values into the work done equation to calculate

$W = 1607 \times 6.0$

$W = 9.6 \times 10^{3} J$

Therefore, the correct answer is D

Examiner Tip

A common exam mistake is choosing the incorrect force which is not parallel to the direction of movement of an object. You may have to resolve the force vector to find the component that is parallel. The force may not always be in the same direction as the movement, as shown in the worked example.

Work & Energy (CIE A Level Physics)

Revision Note

Work done

Man pushing a block

Worked example

Examiner Tip

You've read 0 of your 10 free revision notes

Unlock more, it's free!

Join the 100,000+ Students that ❤️ Save My Exams

Author: Leander