Revision NotesExam QuestionsPast Papers
A LevelPhysicsCIERevision Notes5. Work, Energy & Power5.1 Energy ConservationDerivation of P = Fv

Syllabus Edition

First teaching 2023

First exams 2025

|

Derivation of P = Fv (CIE A Level Physics)

Revision Note

Katie M

Author

Katie M

Last updated

Derivation of P = Fv

  • The power delivered to a moving object is described by the equation:

P space equals space F v

  • Where:
    • P = power in watts (W)
    • F = force in newtons (N)
    • v = velocity in metres per second (m s-1)

  • This equation is only relevant where a constant force moves a body at constant velocity
  • Power is delivered to the object by a force in order to produce an acceleration
  • The force must be applied in the same direction as the velocity

Derivation

  • Power is the rate of doing work

P space equals fraction numerator space W over denominator t end fraction

  • Work is done when a force moves an object over a distance

W space equals space F s

  • At a constant velocity, the distance moved by the object can be described as:

d space equals space v t

  • Substituting this into the work done equation gives:

W space equals space F v t

  • And substituting this into the power equation gives:

P space equals space fraction numerator F v down diagonal strike t over denominator down diagonal strike t end fraction

P space equals space F v

Worked example

A lorry moves up a road that is inclined at 14.5° to the horizontal.

The lorry has mass 3500 kg and is travelling at a constant speed of 9.4 m s-1. The force due to air resistance is negligible.

Calculate the useful power from the engine to move the lorry up the road.

Answer:

Step 1: List the known quantities

  • Mass, m = 3500 kg
  • Speed, v = 9.4 m s-1
  • Angle of incline = 14.5°

Step 2: State the equation for power in motion

P space equals space F v

Step 3: Calculate the component of the applied force which overcomes the weight

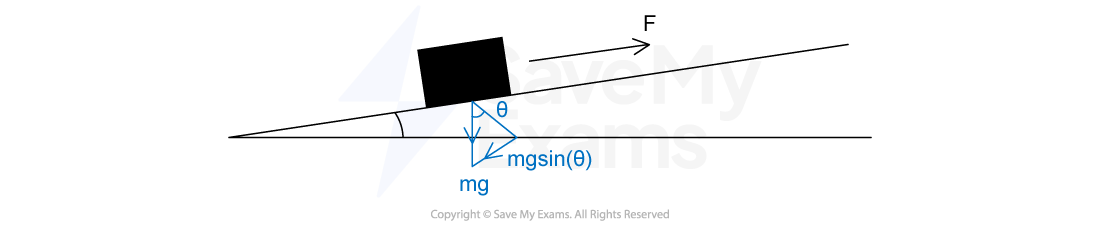
5-1-5-worked-example-p-fv-2-cie-new

F space equals space m g sin theta

F space equals space 3500 space cross times space 9.81 space cross times space sin open parentheses 14.5 close parentheses

F space equals space 8596.8 space straight N

Step 4: Substitute the known values into the power equation to calculate

P space equals space 8596.8 space cross times space 9.4

P space equals space 81 space 000 space straight W space open parentheses 2 space straight s. straight f. close parentheses

Examiner Tip

The force represented in exam questions will often be a drag force. Whilst this is in the opposite direction to its velocity, remember the force needed to calculate the power is equal to (or above) this drag force to overcome it therefore you equate it to that value.

You've read 0 of your 5 free revision notes this week

Sign up now. It’s free!

Join the 100,000+ Students that ❤️ Save My Exams

the (exam) results speak for themselves:

    Test yourself

    Did this page help you?

    Previous:PowerNext:Gravitational Potential Energy
    Katie M

    Author: Katie M

    Expertise: Physics

    Katie has always been passionate about the sciences, and completed a degree in Astrophysics at Sheffield University. She decided that she wanted to inspire other young people, so moved to Bristol to complete a PGCE in Secondary Science. She particularly loves creating fun and absorbing materials to help students achieve their exam potential.